- 図形の重心を求める方法
- 図形の重心を求めるプログラム
こんにちは、Youta(@youta_blog)です。
今回は、図形の重心を求めるお話です。
あなたは学生時代、次のような問題を見たことはありますか?
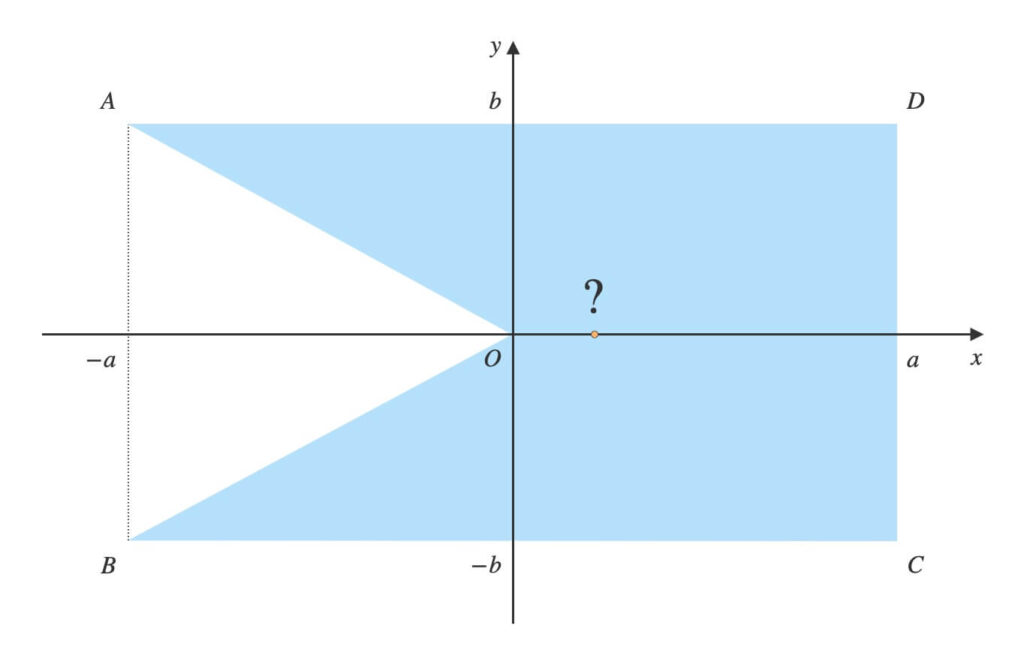
横の長さ\(×\)縦の長さが\(2a×2b\)の均質な長方形板\(ABCD\)がある。
板から\(\triangle{AOB}\)部分を切り抜いた。
残りの図形の重心\(G\)の座標\((x_G,\ y_G)\)を求めよ。
解法を忘れてしまったり、そもそもどう解けばいいかわからない…という方が多いのではないでしょうか。
でもご安心ください!
記事を読めば、この問題の対処法を学べます。
合わせて、コンピューターに自動で解かせるためのプログラムもご紹介します。
- 密度が一様
- 自己交差がない
Contents
図形の重心を求める方法
始めに冒頭の問題の答えを示します。

\((x_G,\ y_G) = (\frac{2}{9}a,\ 0)\)

まあ\(x\)軸上だよね〜。
求め方知らんけど。

丁寧に解説しますね。
手順は簡単。\(4\)ステップで求められます。
図形を複数の三角形に分ける
重心を求めたい図形をバラバラにして、三角形を作り出します。
基準点から左回り(反時計回り)に点を結んで三角形を作るのがポイントです。
基準点はどこでも構いません。

ちょっとよくわかんないわ〜。

\(2\)つの場合で解説しましょう。
- \(O\)が基準: 図形内を三角形で分ける場合
- \(A\)が基準: 図形外に三角形ができる場合
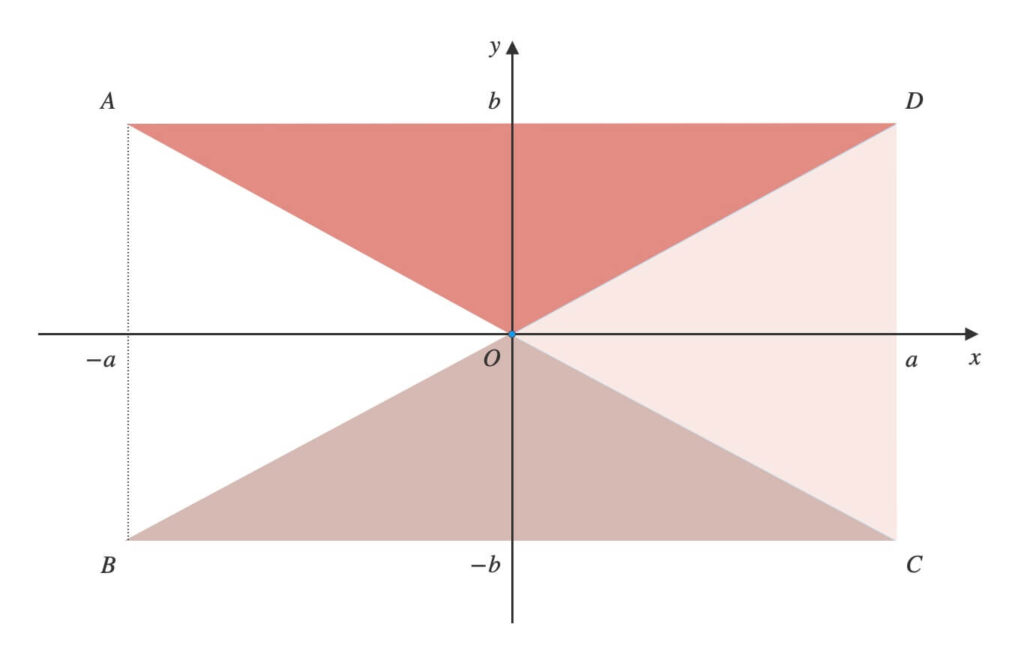
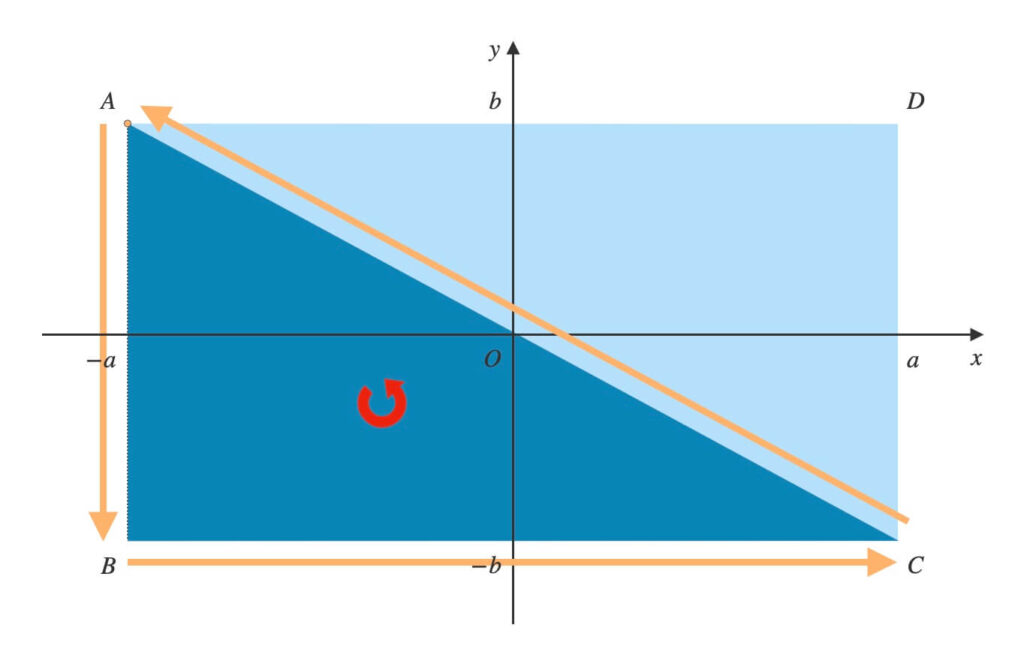
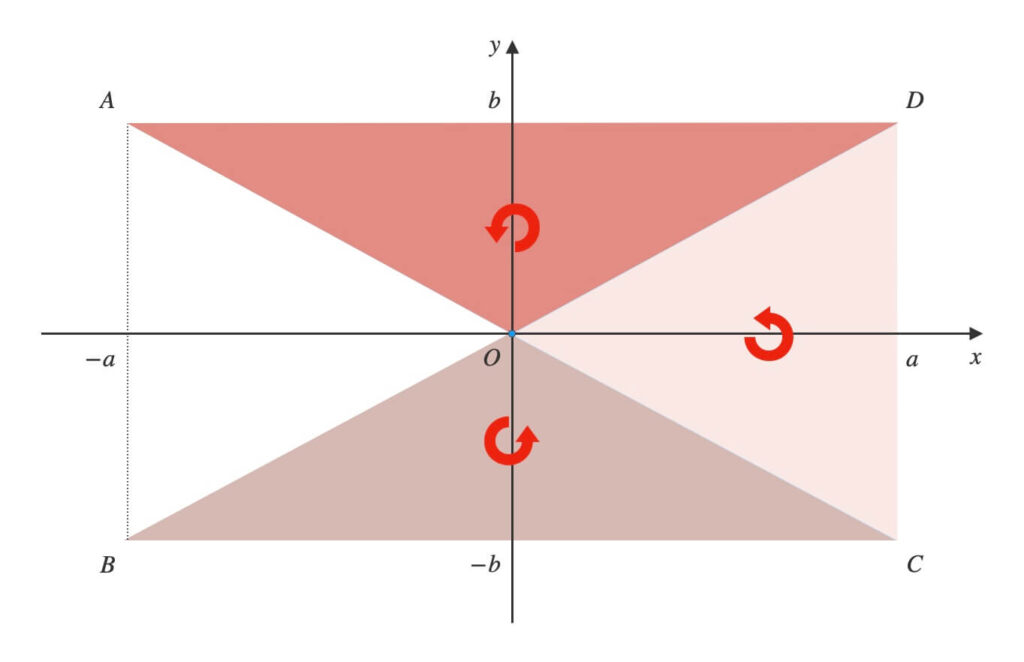
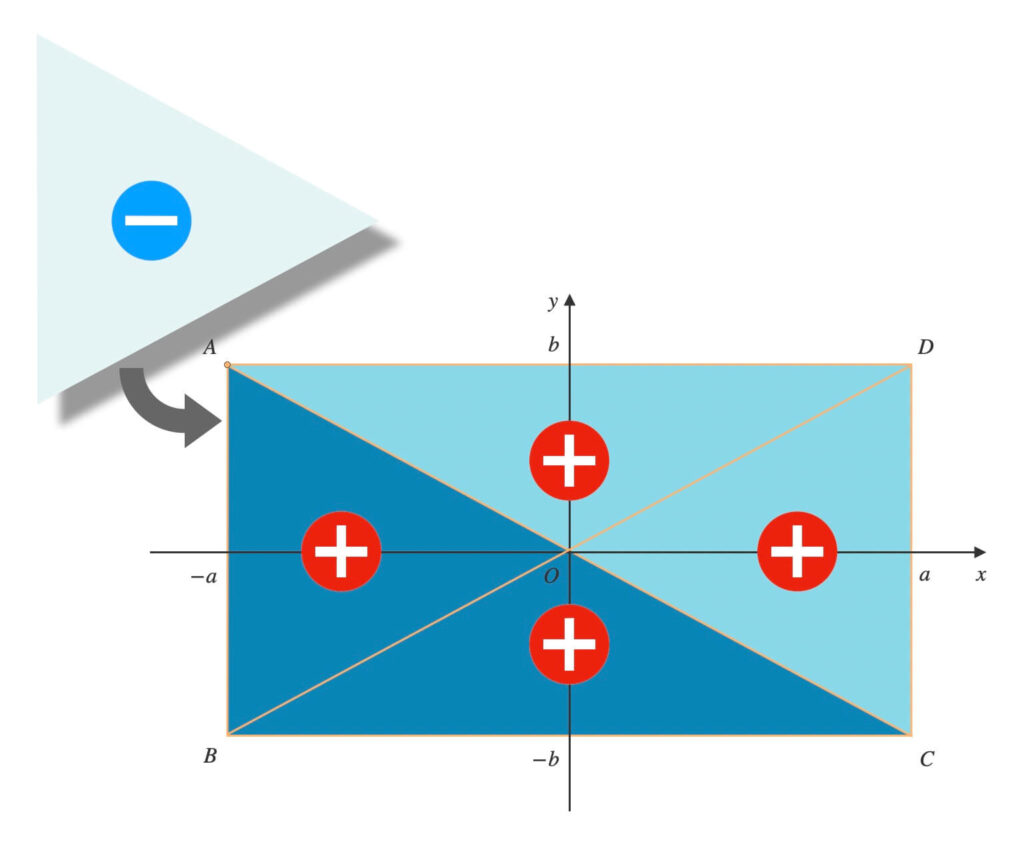
点\(O\)から反時計回りに順に頂点を結び、三角形を作ります。
\(O \rightarrow B \rightarrow C\)と辿り、\(\triangle{OBC}\)ができます。
\(O \rightarrow C \rightarrow D\)と辿り、\(\triangle{OCD}\)ができます。
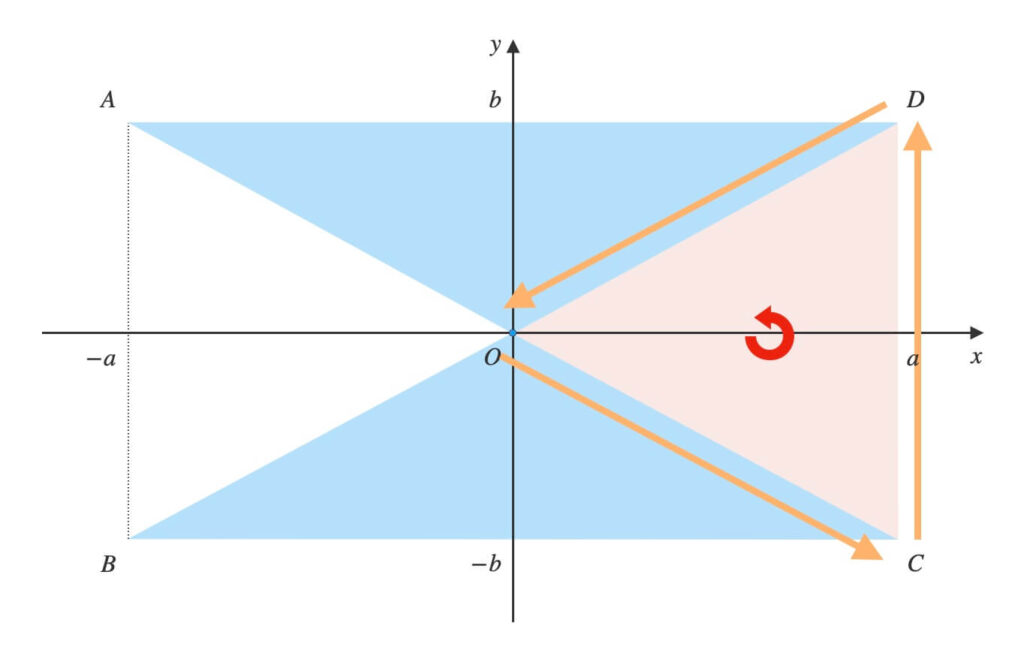
\(O \rightarrow D \rightarrow A\)と辿り、\(\triangle{ODA}\)ができます。
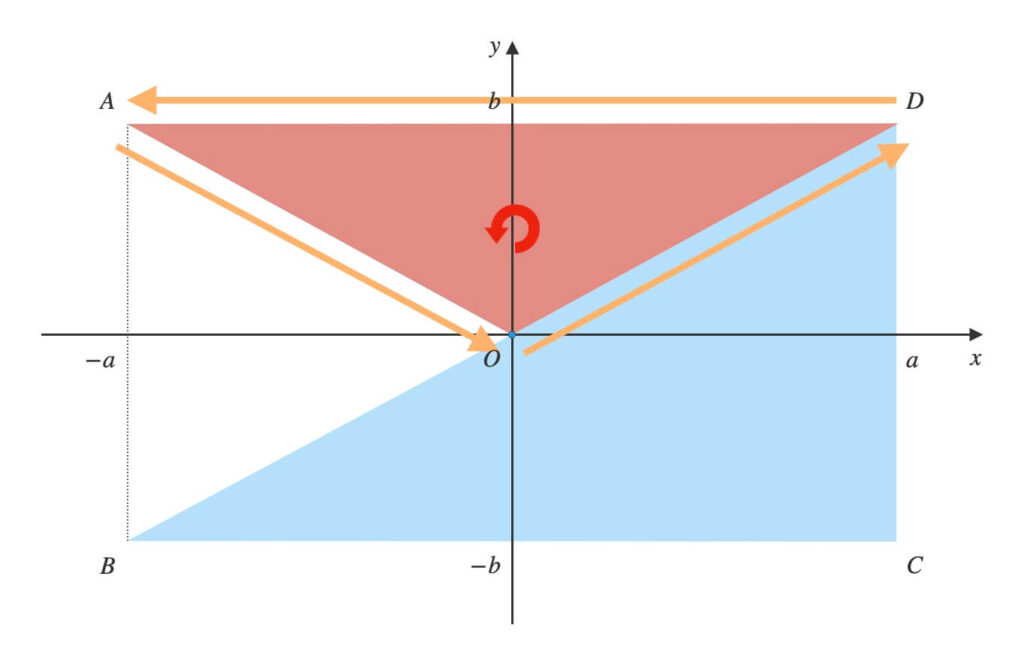
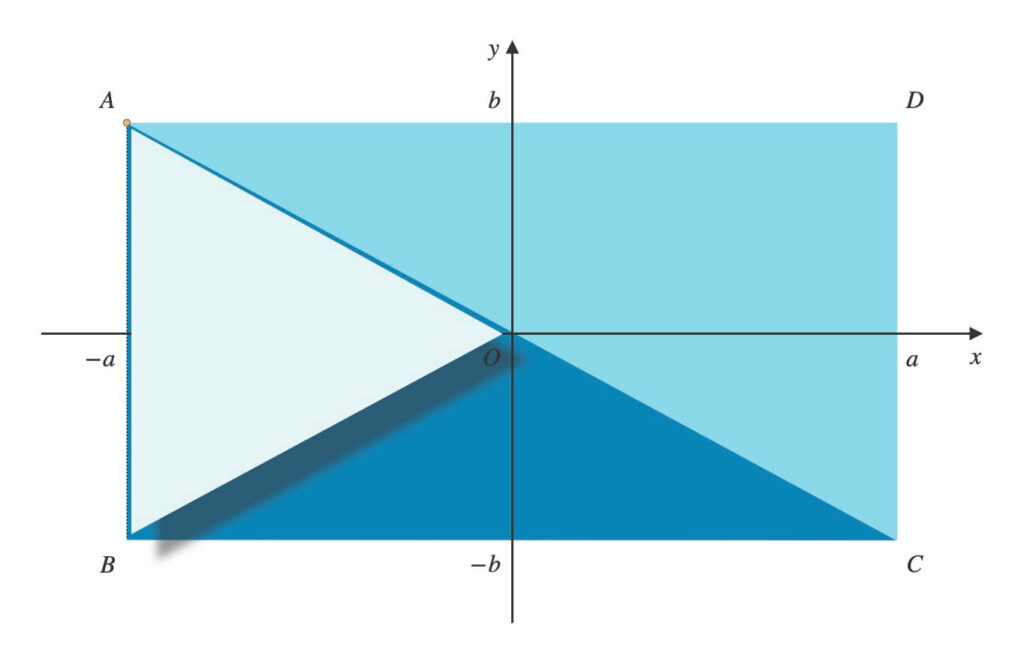
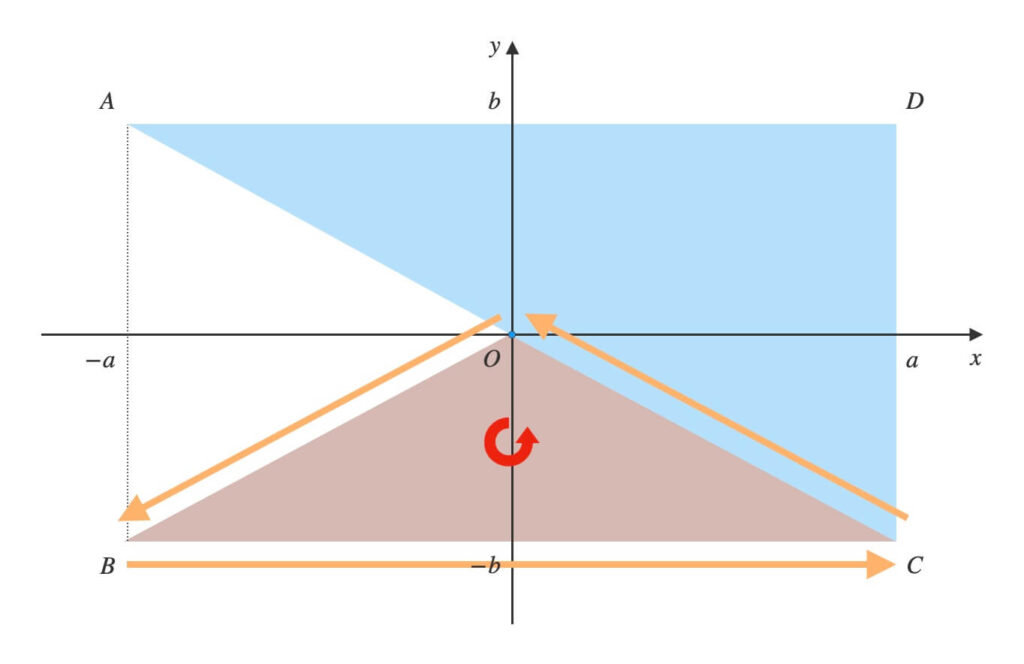
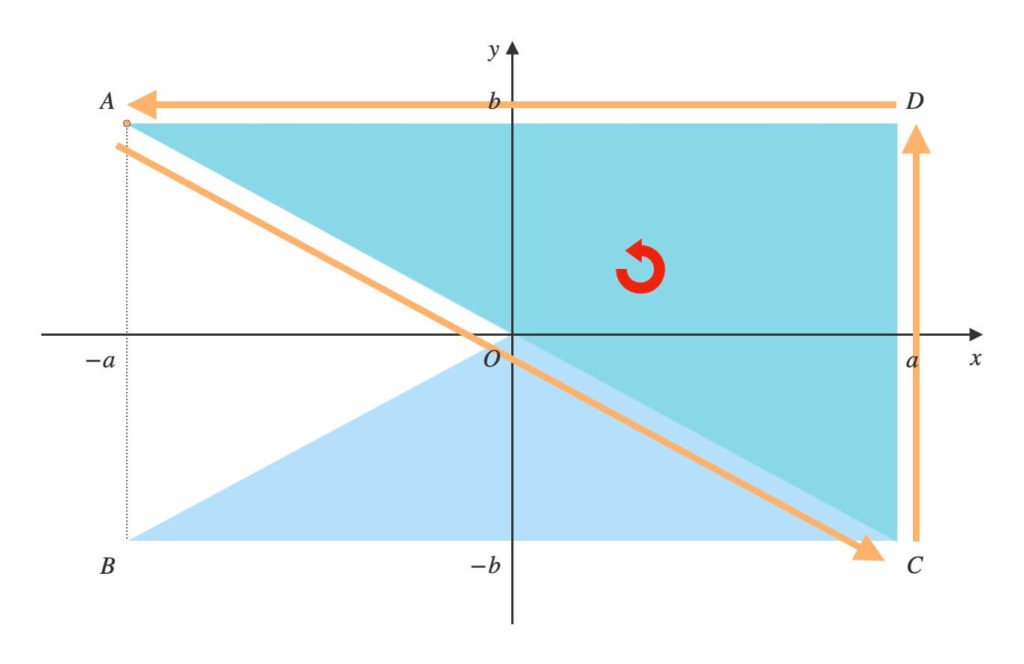
点\(A\)から反時計回りに順に頂点を結び、三角形を作ります。
\(A \rightarrow O \rightarrow B\)と辿り、\(\triangle{AOB}\)ができます。
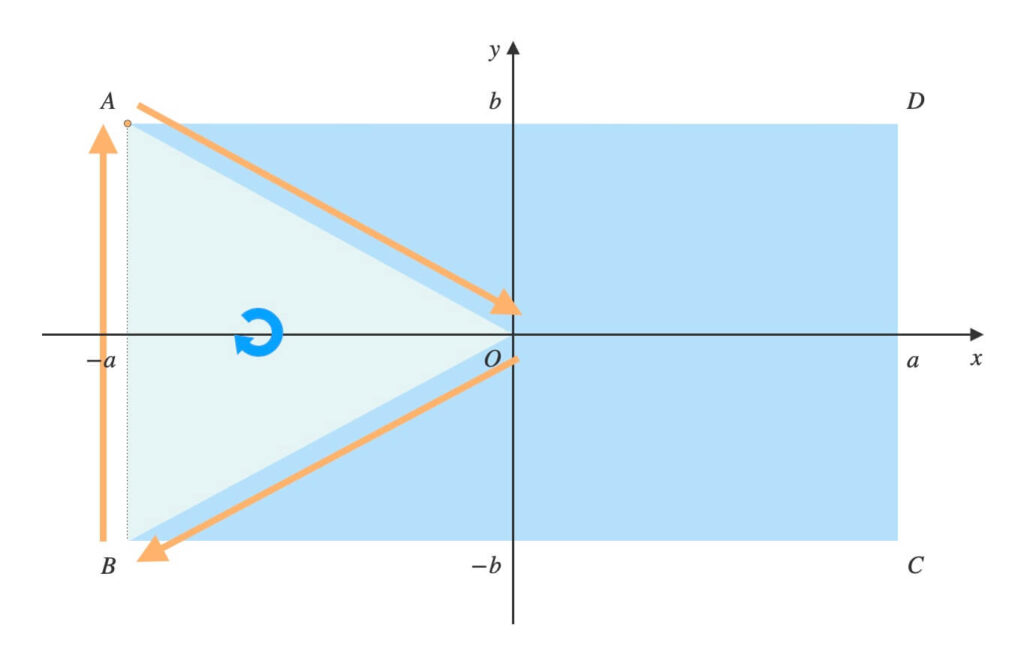

\(\triangle{AOB}\)って図形の外じゃん!

反時計回りに頂点を繋いでいるのであれば、全く問題ありません。
最初は戸惑うかも知れません。
ですが、最後は点\(O\)が基準点の場合と同様の結果となるのでご安心ください。
\(A \rightarrow B \rightarrow C\)と辿り、\(\triangle{ABC}\)ができます。
\(A \rightarrow C \rightarrow D\)と辿り、\(\triangle{ACD}\)ができます。
各三角形の面積を求める
分割された各三角形の面積を求めます。
三角形の頂点から面積を求めるには、次の公式を利用します。
ですが、重心を求めるには符号付き(\(+\) or \(-\))の面積を利用します。

面積がマイナスってどゆこと?
例えば、頂点を\(A \rightarrow B \rightarrow C\)の順に辿る場合。
面積は、経路が反時計回りなら正とし、時計回りなら負とします。
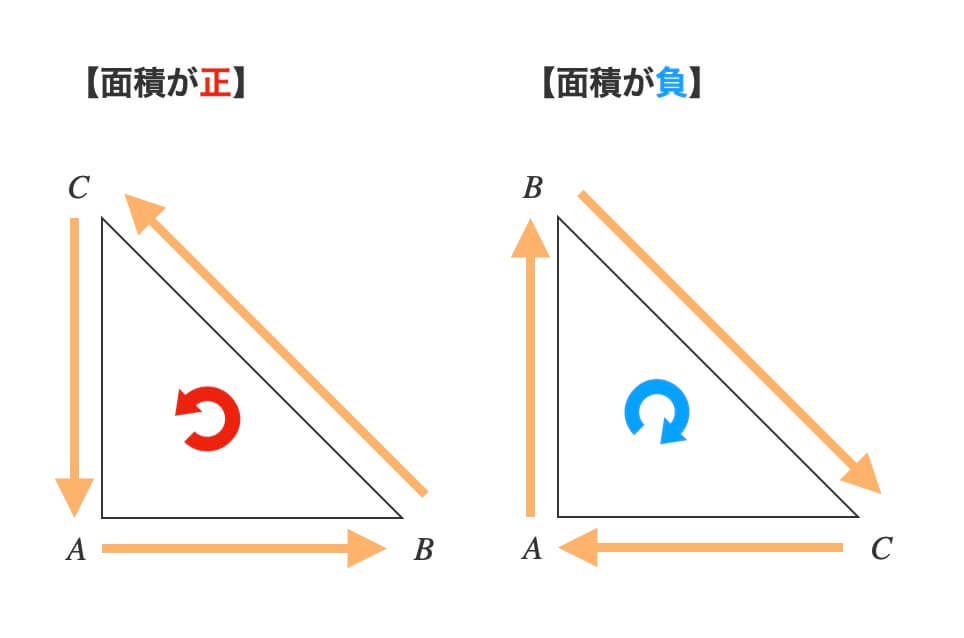
経路がどちら回りかは、外積\(\overrightarrow{AB} \times \overrightarrow{AC}\)の\(z\)成分の符号で判定します。
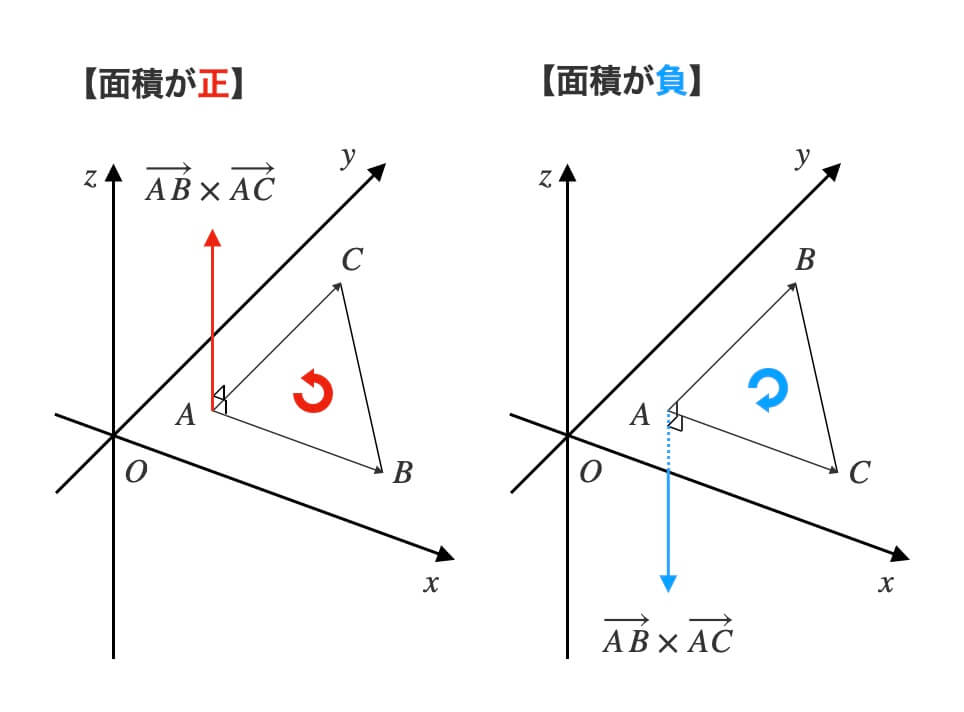
先程と同様、次の\(2\)つの場合で面積の求め方を見ていきましょう。
- \(O\)が基準: 面積がすべて正の場合
- \(A\)が基準: 面積が負になる場合
\(\triangle{OBC}\)・\(\triangle{OCD}\)・\(\triangle{ODA}\)の面積を求めます。
どの三角形も経路が反時計回りなので、面積が正ですね。
冗長になるため、\(\triangle{OBC}\)の場合の計算手順だけをお載せします。
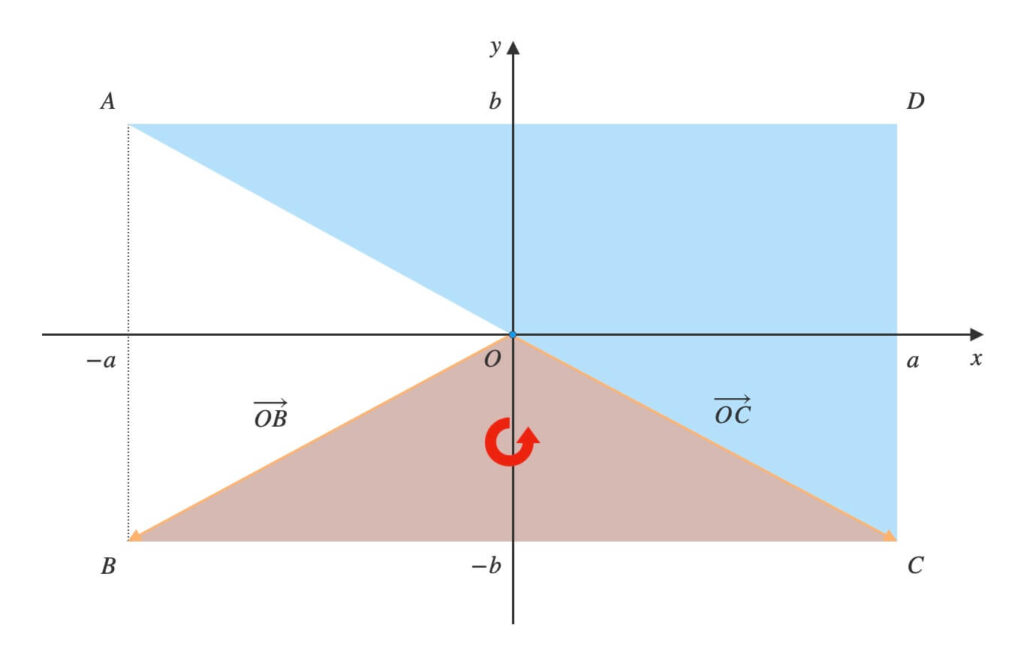
下記の公式を利用して、外積を求めます。
\(\overrightarrow{OB} \times \overrightarrow{OC} = (x,\ y,\ z)\)とする。
\(\overrightarrow{OB} = (-a,\ -b,\ 0)\), \(\overrightarrow{OC} = (a,\ -b,\ 0)\)より、
\(x = -b \cdot 0\ – 0 \cdot (-b) = 0\)
\(y = 0 \cdot a\ – (-a) \cdot 0 = 0\)
\(z = (-a) \cdot (-b)\ – (-b) \cdot a = 2ab\)
よって、\(\overrightarrow{OB} \times \overrightarrow{OC} = (0,\ 0,\ 2ab)\)
また、\(\overrightarrow{OB} \times \overrightarrow{OC}\)の\(z\)成分は正である。
\(|\overrightarrow{OB} \times \overrightarrow{OC}| = 2ab\)であるから、
\(\triangle{OBC}の面積 = \frac{1}{2}|\overrightarrow{OB} \times \overrightarrow{OC}| = ab\)
他の三角形の面積も同じ手順で求められます。
- \(\triangle{OBC}\): \(ab\)
- \(\triangle{OCD}\): \(ab\)
- \(\triangle{ODA}\): \(ab\)
つまり、残った板の面積は\(3ab\)です。
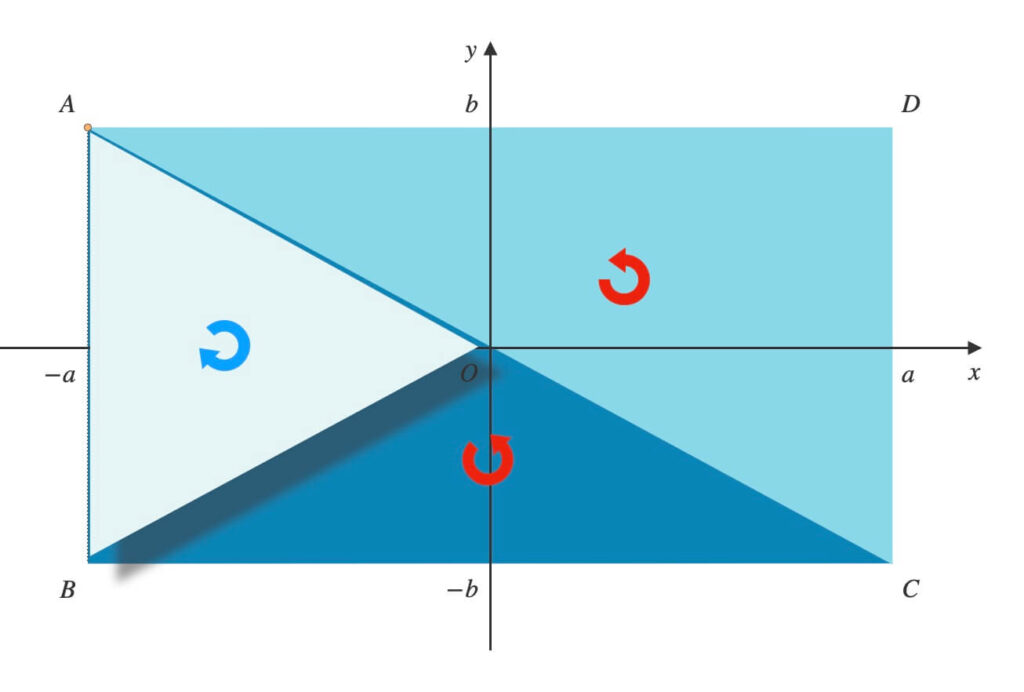
\(\triangle{AOB}\)・\(\triangle{ABC}\)・\(\triangle{ACD}\)の面積を求めます。
\(\triangle{AOB}\)は経路が時計回りなので、その面積を負として扱います。
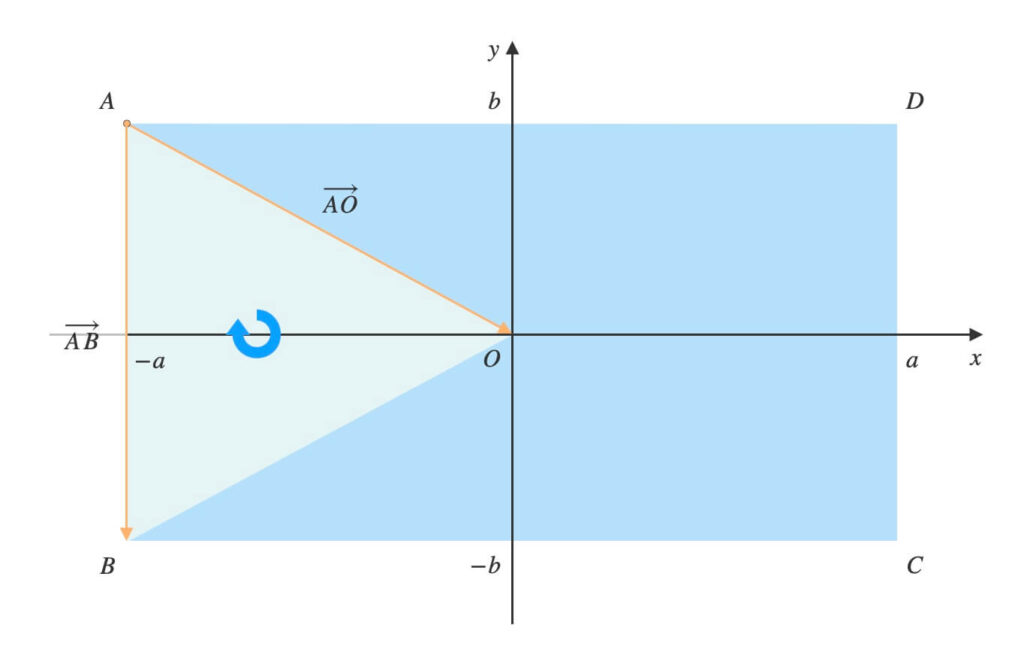
せっかくなので\(\triangle{AOB}\)の面積だけ一緒に求めましょう。
\(A = (-a,\ b,\ 0)\),
\(O = (0,\ 0,\ 0)\),
\(B = (-a,\ -b,\ 0)\)より、
\(\overrightarrow{AO} \times \overrightarrow{AB} = (x,\ y,\ z)\)とする。
\(x = -b \cdot 0\ – 0 \cdot (-2b) = 0\)
\(y = 0 \cdot 0\ – a \cdot 0 = 0\)
\(z = a \cdot (-2b)\ – (-b) \cdot 0 = -2ab\)
よって、\(\overrightarrow{OB} \times \overrightarrow{OC} = (0,\ 0,\ -2ab)\)
また、\(\overrightarrow{AO} \times \overrightarrow{AB}\)の\(z\)成分は負である。
\(|\overrightarrow{OB} \times \overrightarrow{OC}| = 2ab\)であるから、
\(\triangle{OBC}の面積 = \frac{1}{2}|\overrightarrow{OB} \times \overrightarrow{OC}| = ab\)
符号を考えると、\(\triangle{OBC}の面積 = -ab\)
他の三角形は経路が反時計回りなので、先程と同様に計算できます。
- \(\triangle{AOB}\): \(-ab\)
- \(\triangle{ABC}\): \(2ab\)
- \(\triangle{ACD}\): \(2ab\)

マイナスの面積で本当にいいの?

はい。むしろ負の面積があるので、辻褄が合うんですよ。
残りの板の面積は\(3ab\)でしたね。
試しに\(\triangle{AOB}\)・\(\triangle{ABC}\)・\(\triangle{ACD}\)の面積を全部足してみましょう。
\(3ab\)ピッタリです。
\(\triangle{ABC}\)の余分な面積を、\(\triangle{AOB}\)の負の面積で相殺したんですね。

へーよくできてるね。
各三角形の重心を求める
分割した各三角形の重心を求めます。
三角形の各頂点の座標から、その重心座標を求める公式です。
頂点の座標さえ分かれば、重心は機械的に計算できます。
\(3\)つの座標の平均なのですから。
基準点が\(O\)の場合。
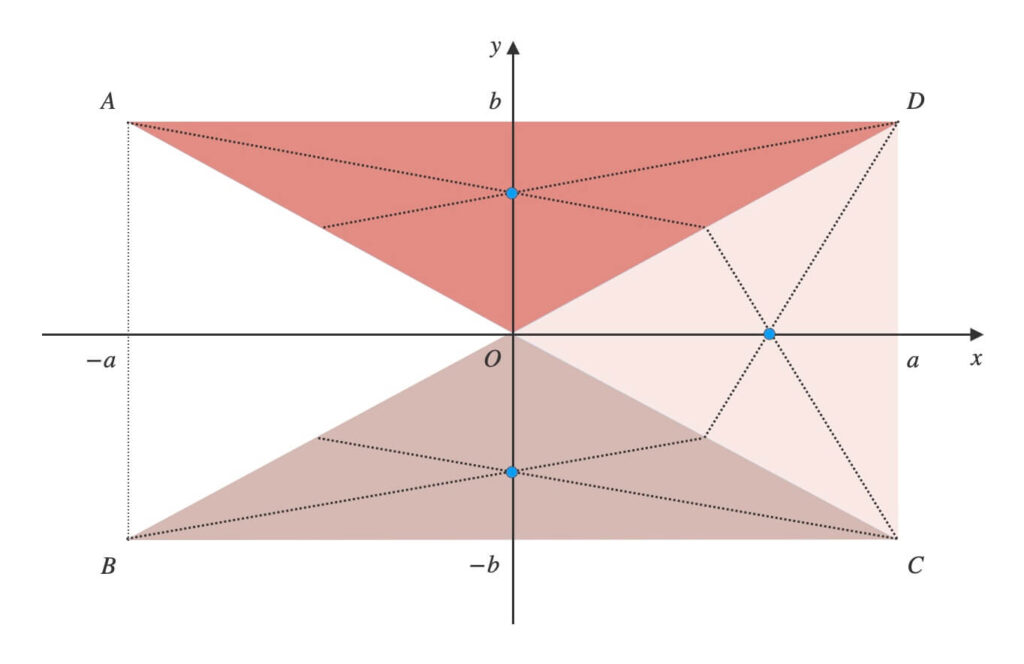
- \(\triangle{OBC}\): \((0,\ -\frac{2}{3}b)\)
- \(\triangle{OCD}\): \((\frac{2}{3}a,\ 0)\)
- \(\triangle{ODA}\): \((0,\ \frac{2}{3}b)\)
基準点が\(A\)の場合。
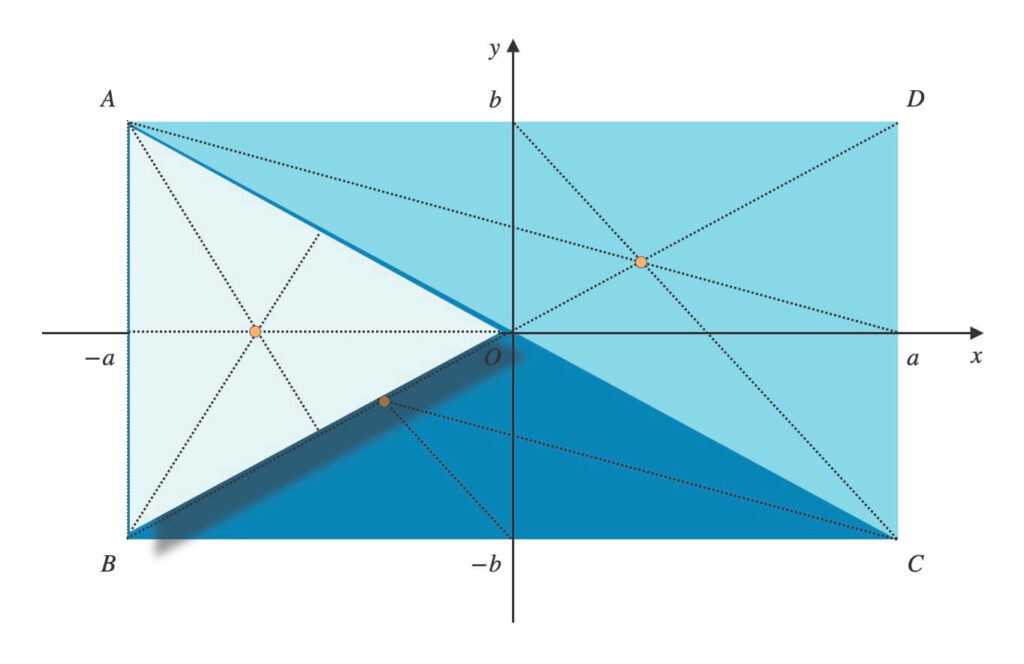
- \(\triangle{AOB}\): \((-\frac{2}{3}a,\ 0)\)
- \(\triangle{ABC}\): \((-\frac{a}{3},\ -\frac{b}{3})\)
- \(\triangle{ACD}\): \((\frac{a}{3},\ \frac{b}{3})\)
各三角形の質量を求める
板の密度を\(\rho\)・厚みを\(h\)として、各三角形の質量を計算します。
質量 \(=\) 密度 \(\cdot\) 体積であり、
体積 \(=\) 面積 \(\cdot\) 厚みです。
よって、質量 \(=\) 密度 \(\cdot\) 面積 \(\cdot\) 厚みです。
- \(O\)が基準: 質量がすべて正の場合
- \(A\)が基準: 質量が負になる場合
\(\triangle{OBC}\)・\(\triangle{OCD}\)・\(\triangle{ODA}\)の質量を求めます。
質量 \(=\) 密度 \(\cdot\) 面積 \(\cdot\) 厚み
この式にパラメータを代入します。
- \(\triangle{OBC}\): \(\rho ab h\)
- \(\triangle{OCD}\): \(\rho ab h\)
- \(\triangle{ODA}\): \(\rho ab h\)
どの三角形にも同じ強さの重力が働くイメージです。
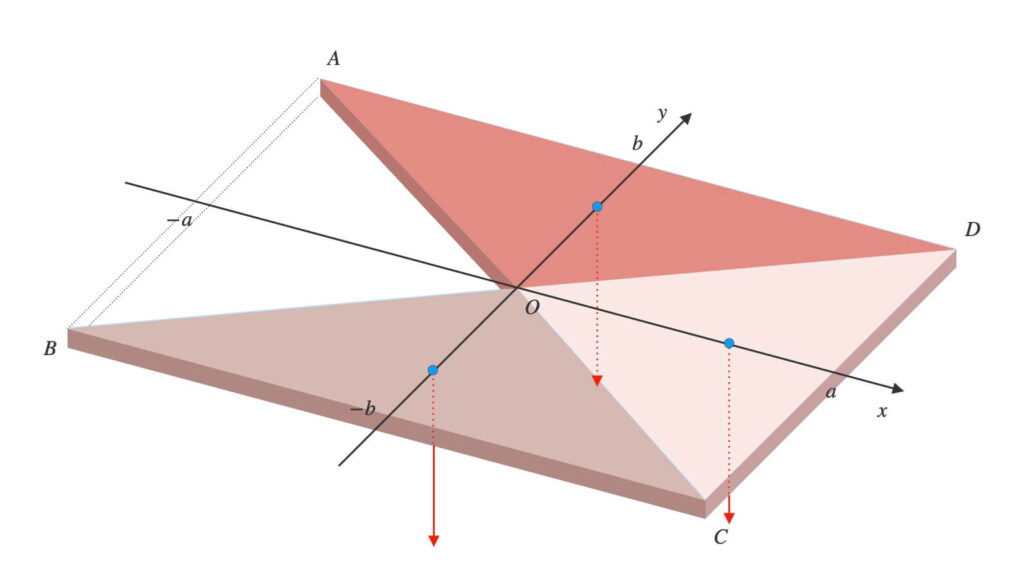
\(\triangle{AOB}\)・\(\triangle{ABC}\)・\(\triangle{ACD}\)の質量を求めます。
質量 \(=\) 密度 \(\cdot\) 面積 \(\cdot\) 厚み
この式にパラメータを代入します。
- \(\triangle{AOB}\): \(-\rho ab h\)
- \(\triangle{ABC}\): \(2\rho ab h\)
- \(\triangle{ACD}\): \(2\rho ab h\)

負の質量っておかしくない?

現実にはありえませんが、計算上では全く問題ありません。
\(\triangle{AOB}\)だけ上向きに重力がかかる感じです。
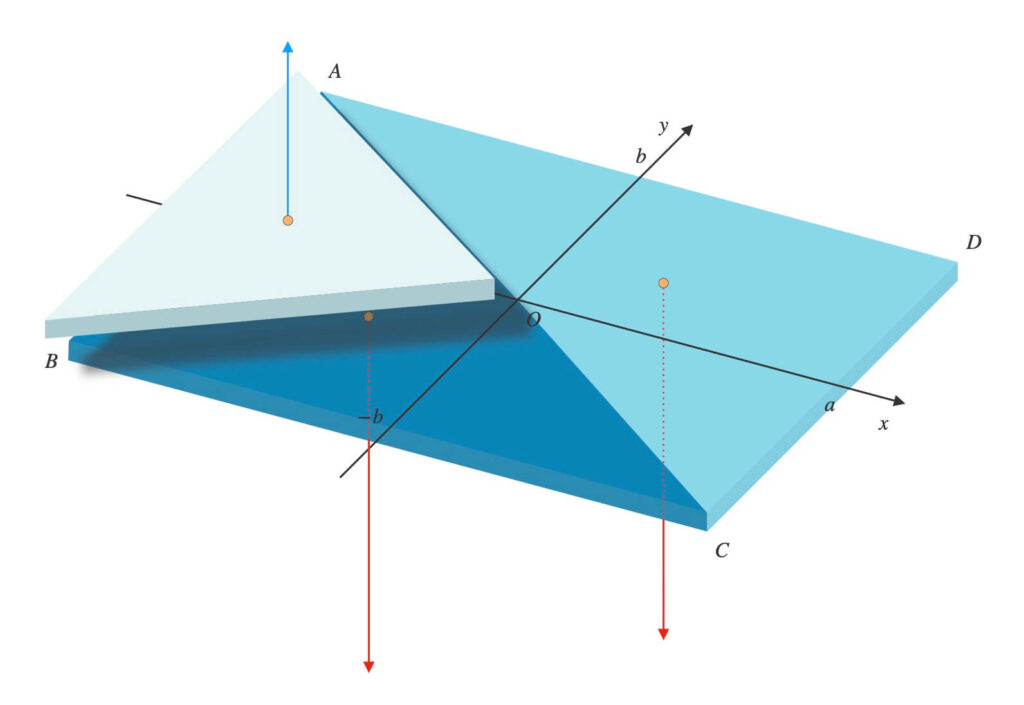
図形全体の重心を求める
準備が整ったので、全体の重心を求めます。
重心を求める公式を利用します。
最後も\(2\)つの場合に分けて説明します。
- \(O\)が基準: 質点に下に力がかかる場合
- \(A\)が基準: 質点に上に力がかかる場合
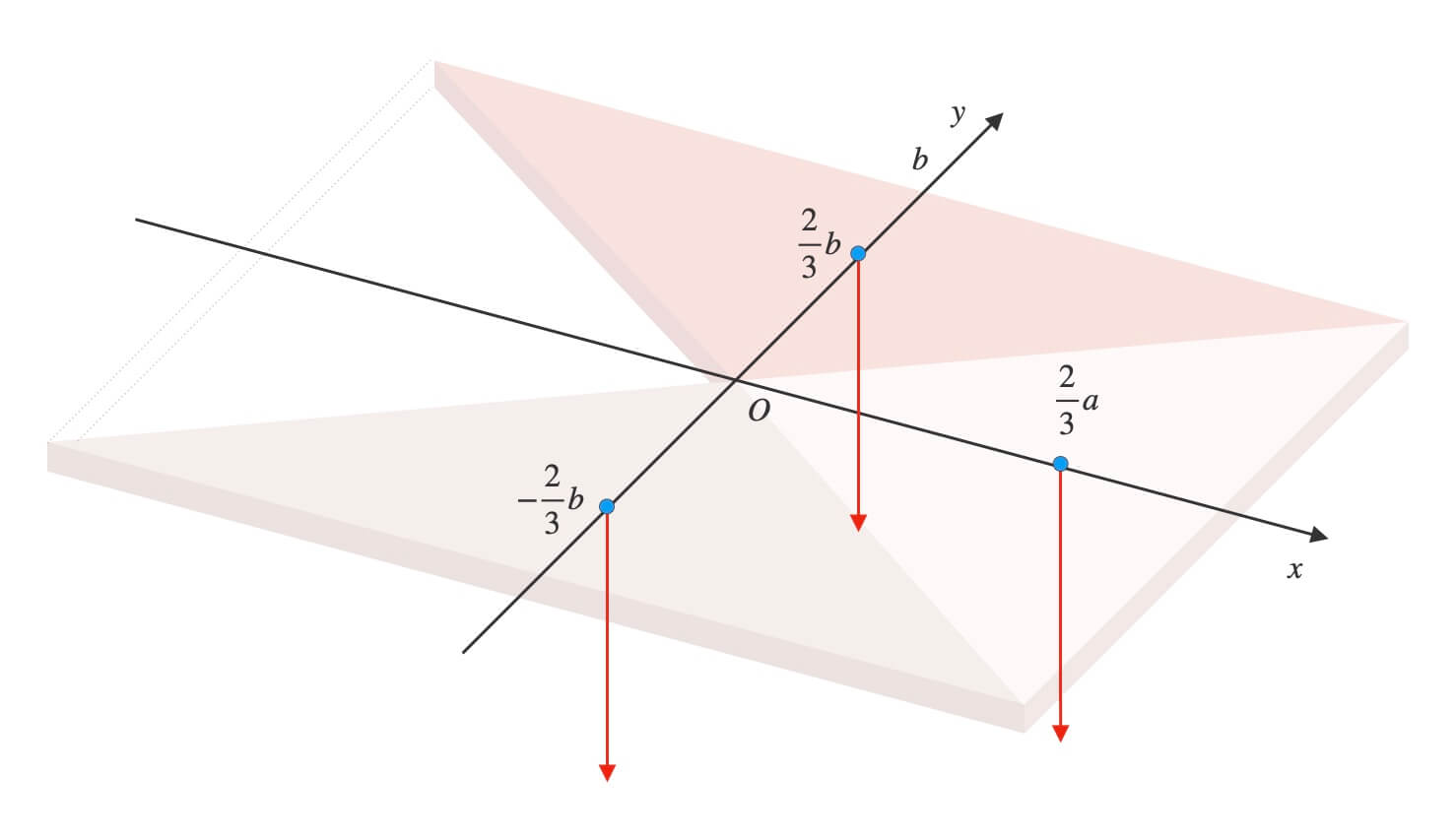
各三角形の重心の位置に、質点が存在すると考えます。
では、全体の重心\(x_G, y_G\)を計算しましょう。
座標平面上の\(3\)点
\((0,\ -\frac{2}{3}b)\), \((\frac{2}{3}a,\ 0)\), \((0,\ \frac{2}{3}b)\)
に、質量が\(\rho abh\)の質点がある。
この質点系の重心の座標\((x_G,\ y_G)\)は、
\((x_G,\ y_G) = (\frac{2}{9}a,\ 0)\)
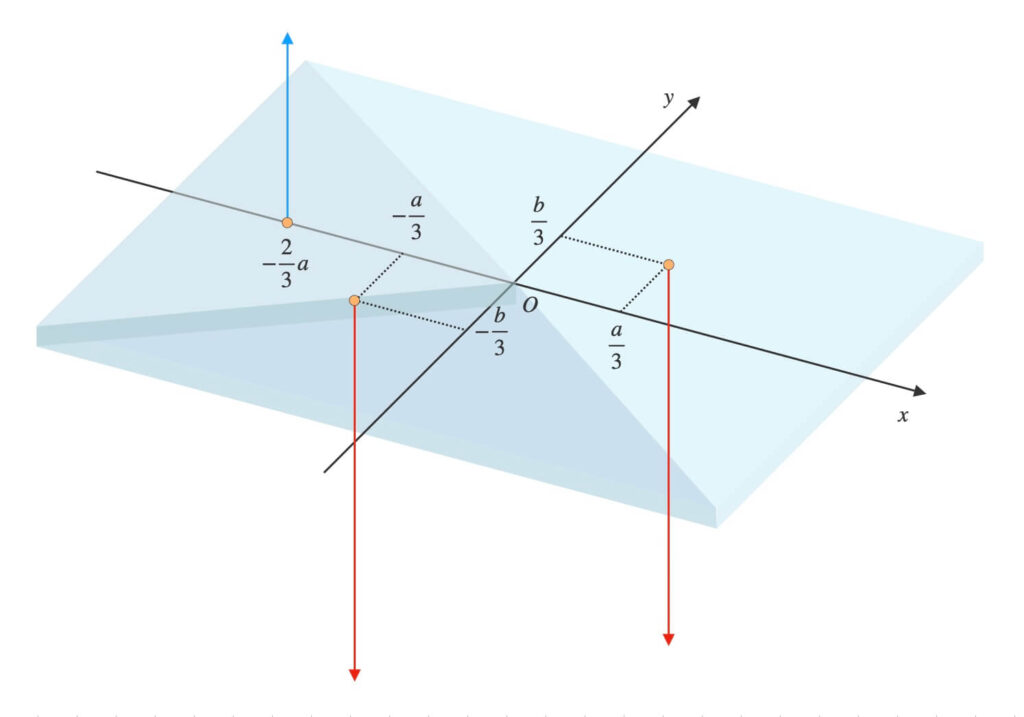
負の質量がありますが、構いません。
\(O\)が基準点の時と同様の手順です。
では、全体の重心\(x_G, y_G\)を計算しましょう。
座標平面上の\(3\)点
\((0,\ -\frac{2}{3}a)\), \((-\frac{a}{3},\ -\frac{b}{3})\), \((\frac{a}{3},\ \frac{b}{3})\)
に質点がある。
各質点はそれぞれ\(-\rho abh\), \(2\rho abh\), \(2\rho abh\)の質量を持つ。
よって、この質点系の重心の座標\((x_G,\ y_G)\)は、
\((x_G,\ y_G) = (\frac{2}{9}a,\ 0)\)

点\(O\)が基準のときと一緒だね!
図形の重心を求めるプログラム
実装例
def triangulate(coords):
# 座標のリストを平坦化
coords = flatten(coords)
# 座標の数を計算
coord_len = len(coords) // 2
# 三角形の数を計算
triangle_num = coord_len - 2
# 三角形の座標を格納する空のリストを初期化
result = []
# 三角形の座標を作成するための繰り返し処理
for i in range(triangle_num):
j = (i + 1) * 2
# 各三角形の座標を抽出
triangle_coords = [
[coords[0], coords[1]],
[coords[j + 0], coords[j + 1],
[coords[j + 2], coords[j + 3],
]
result.append(triangle_coords)
# 三角形の座標のリストを返却
return result
def flatten(sequence):
result = []
for item in sequence:
if isinstance(item, (list, tuple, range, dict, set, frozenset)):
result.extend(flatten(item))
else:
result.append(item)
return result
triangulate関数は、三角形の座標を生成します。
| 変数名 | データ型 | 必須 / 任意 | 説明 |
|---|---|---|---|
coords | リスト・タプル | 必須 | 複数の座標 座標は座標平面内に限る。 |
triangulate関数の引数下記の形式に対応しています。
coords_a = [x1, y1, x2, y2, …, xn, yn] # 一次元リスト
coords_b = (x1, y1, x2, y2, …, xn, yn) # 一次元タプル
coords_c = [[x1, y1], [x2, y2], …, [xn, yn]] # ネストされたリスト(タプル)
triangulate(coords_◯) # OK
| データ型 | 説明 |
|---|---|
| リスト | 三角形の頂点の座標 |
triangulate関数の戻り値形式に関しては、下記をご覧ください。
coords = [x1, y1, x2, y2, …, xn, yn]
result = triangulate(coords)
print(result)
# [[[x1, y1], [x2, y2], [x3, y3]], [[x1, y1], [x3, y3], [x4, y4]], …, [[x1, y1], [xn-1, yn-1], [xn, yn]]]
numpyの配列に変換すると分かりやすいでしょう。
import numpy as np
print(np.array(result))
# [[[x1 y1]
# [x2 y2]
# [x3 y3]]
#
# [[x1 y1]
# [x3 y3]
# [x4 y4]]
#
# [[x1 y1]
# [x4 y4]
# [x5 y5]]
#
# …
#
# [[x1 y1]
# [xn-1 yn-1]
# [xn yn]]]
リスト・タプルを平坦化するflatten関数は、下記をご参照ください。
【Python】リストの平坦化(flatten)処理を徹底解説!
import numpy as np
def get_triangle_area(point_a, point_b, point_c):
# ベクトル演算を行うため、点をNumPy配列に変換
point_a = np.array(point_a)
point_b = np.array(point_b)
point_c = np.array(point_c)
# ベクトルABおよびACを計算
vector_ab = point_b - point_a
vector_ac = point_c - point_a
# ベクトルABおよびACの外積を計算
cross_product = np.cross(vector_ab, vector_ac)
# 外積がz成分のみの場合、符号付き面積を利用
if cross_product.size == 1:
parallelogram_area = cross_product
# 外積が3次元配列の場合、外積の大きさを計算
else:
parallelogram_area = np.linalg.norm(cross_product)
# 三角形の面積(平行四辺形の面積の半分)を返却
return parallelogram_area / 2
get_triangle_area関数は、三角形の面積を求めます。
| 変数名 | データ型 | 必須 / 任意 | 説明 |
|---|---|---|---|
point_a | リスト・タプル | 必須 | 三角形の頂点の座標 座標は座標平面・座標空間に対応。 |
point_b | リスト・タプル | 必須 | 三角形の頂点の座標 座標は座標平面・座標空間に対応。 |
point_c | リスト・タプル | 必須 | 三角形の頂点の座標 座標は座標平面・座標空間に対応。 |
get_triangle_area関数の引数座標平面上の点の際は要素を\(2\)つ、座標空間上の点の際は要素を\(3\)つ含ませます。
要素の数は\(3\)つとも統一させてください。
| データ型 | 説明 |
|---|---|
| 浮動小数点 | 引数point_a〜point_cで囲まれる三角形の面積 |
get_triangle_area関数の戻り値引数point_◯の次元数に応じて、下記の違いがあります。
- 二次元: 符号付き面積
- 三次元: 面積
import numpy as np
def get_triangle_centroid(point_a, point_b, point_c):
# numpy.array型に変換
point_a = np.array(point_a)
point_b = np.array(point_b)
point_c = np.array(point_c)
# 重心を計算
centroid = (point_a + point_b + point_c) / 3
# リストに変換して返す
return centroid.tolist()
get_triangle_centroid関数は、三角形の重心を求めます。
| 変数名 | データ型 | 必須 / 任意 | 説明 |
|---|---|---|---|
point_a | リスト・タプル | 必須 | 三角形の頂点の座標 座標は座標平面・座標空間に対応。 |
point_b | リスト・タプル | 必須 | 三角形の頂点の座標 座標は座標平面・座標空間に対応。 |
point_c | リスト・タプル | 必須 | 三角形の頂点の座標 座標は座標平面・座標空間に対応。 |
get_triangle_centroid関数の引数座標平面上の点の際は要素を\(2\)つ、座標空間上の点の際は要素を\(3\)つ含ませます。
要素の数は\(3\)つとも統一させてください。
| データ型 | 説明 |
|---|---|
| リスト | 引数の座標で囲まれる三角形の重心の座標 次元は引数に一致する。 |
get_triangle_centroid関数の戻り値
import numpy as np
def get_centroid(coords):
# 座標を三角形に分割
triangles = triangulate(coords)
# 各三角形の重心・符号付き面積を計算
centroids = np.array([get_triangle_centroid(*triangle) for triangle in triangles])
signed_areas = np.array([get_triangle_area(*triangle) for triangle in triangles])
# 図形の総面積を計算
area = np.sum(signed_areas)
# 符号付き面積を考慮した重心を計算
weighted_centroids = centroids * signed_areas[:, None]
# 図形全体の重心を計算
x = np.sum(weighted_centroids[:, 0]) / area
y = np.sum(weighted_centroids[:, 1]) / area
# 重心の座標を返す
return [x, y]
get_centroid関数は、引数の座標を頂点とする図形の重心を求めます。
| 変数名 | データ型 | 必須 / 任意 | 説明 |
|---|---|---|---|
coords | リスト・タプル | 必須 | 図形の頂点の座標 座標は座標平面内に限る。 |
get_ceontroid関数の引数下記の形式に対応しています。
coords_a = [x1, y1, x2, y2, …, xn, yn] # 一次元リスト
coords_b = (x1, y1, x2, y2, …, xn, yn) # 一次元タプル
coords_c = [[x1, y1], [x2, y2], …, [xn, yn]] # ネストされたリスト(タプル)
get_centroid(coords_◯) # OK
| データ型 | 説明 |
|---|---|
| リスト | 引数の座標で囲まれる図形の重心の座標 |
get_centroid関数の戻り値テスト

このプログラムは、頂点さえ分かれば、どんな多角形の重心でも求められます。
その威力を存分に感じてください。
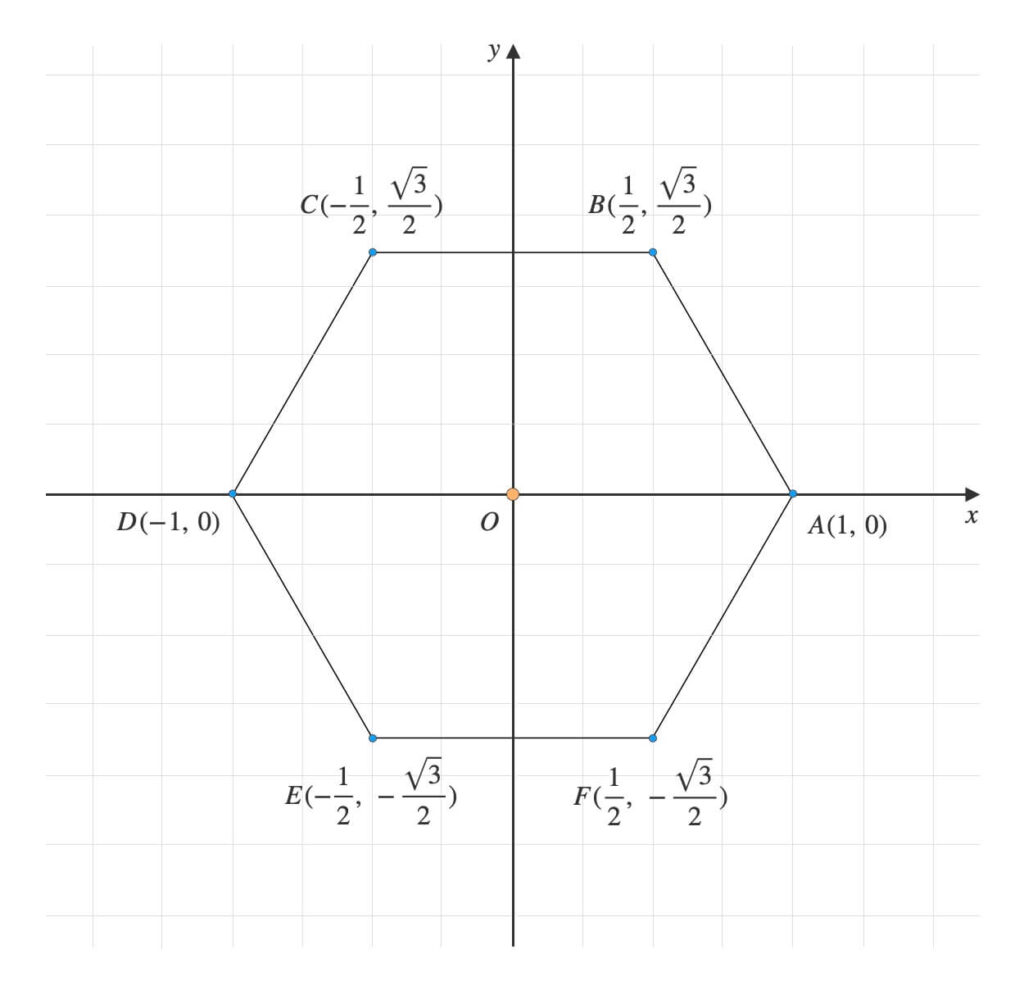
正六角形の重心を取れるか試します。
get_centroid関数の下に、下記のテストコードを書いて実行します。
a = (1, 0)
b = (1/2, np.sqrt(3)/2)
c = (-1/2, np.sqrt(3)/2)
d = (-1, 0)
e = (-1/2, -np.sqrt(3)/2)
f = (1/2, -np.sqrt(3)/2)
coords = (a, b, c, d, e, f)
answer = get_centroid(coords)
print(answer)
実行結果です。
print(answer)
# [0.0, 0.0]
重心は原点ですね。
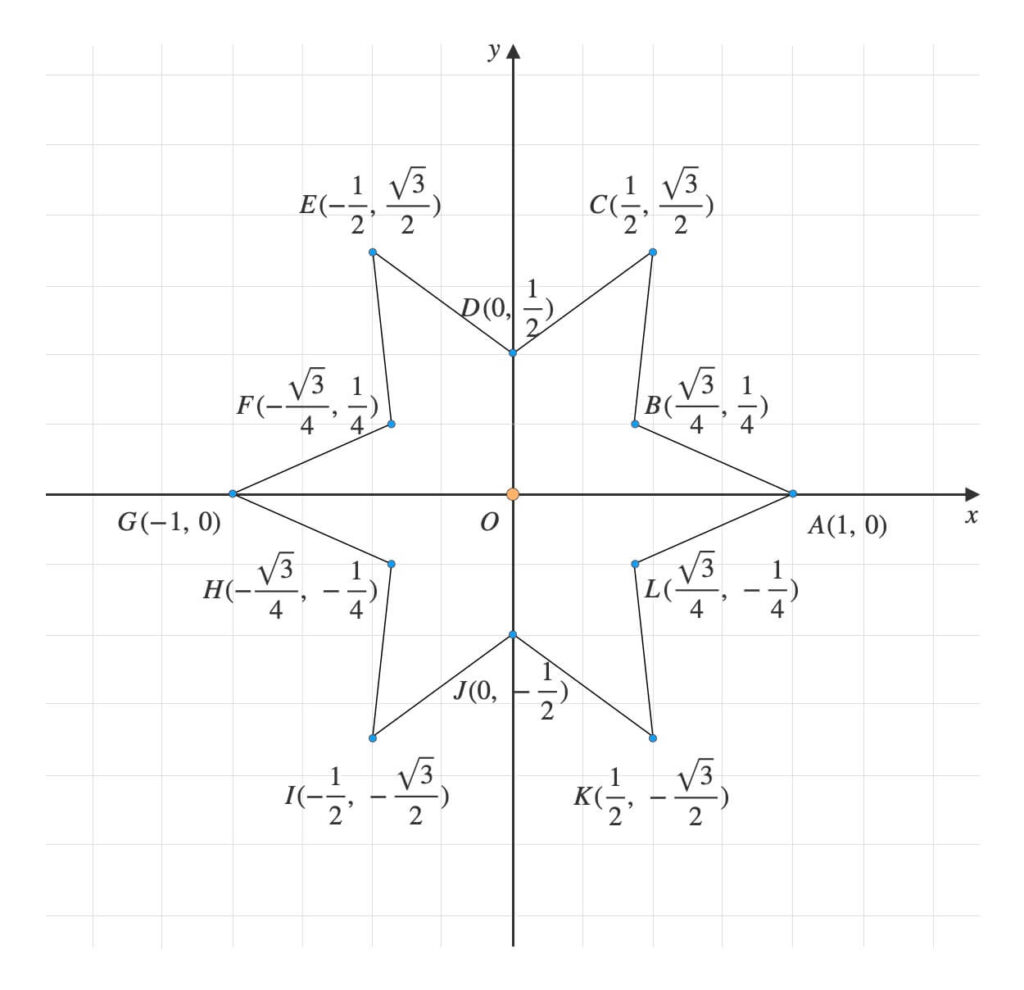
六芒星の重心を取れるか試します。
get_centroid関数の下に、下記のテストコードを書いて実行します。
a = (1, 0)
b = (np.sqrt(3)/4, 1/4),
c = (1/2, np.sqrt(3)/2),
d = (0, 1/2),
e = (-1/2, np.sqrt(3)/2),
f = (-np.sqrt(3)/4, 1/4),
g = (-1, 0),
h = (-np.sqrt(3)/4, -1/4),
i = (-1/2, -np.sqrt(3)/2),
j = (0, -1/2),
k = (1/2, -np.sqrt(3)/2),
l = (np.sqrt(3)/4, -1/4),
coords = (a, b, c, d, e, f, g, h, i, j, k, l)
answer = get_centroid(coords)
print(answer)
実行結果です。
print(answer)
# [-9.251858538542972e-18, 0.0]

やった!バグったね!

嬉しそうですね。
出力結果を確認してみましょう。
[-9.251858538542972e-18, 0.0]の\(x\)座標ですが、後ろにe-18とありますね。
これは、\(e\)の左の数字に\(1^{-18}\)を掛けるのを意味します。
よって、-9.251858538542972e-18 \(=\) -0.000000000000000009251858538542972(\(0\)が\(18\)個)です。
わずかな誤差なので、ほぼ\(0\)と見て良いのではないでしょうか。
したがって、重心はやはり原点です。

な〜んだ、つまんないの〜。
図形の重心を求めるプログラムの活用例
図形をマウスドラッグで回転させるプログラムです。
PythonのGUIライブラリであるTkinterで作りました。
複雑そうですが、仕組みはシンプルです。
クリックした瞬間、図形の頂点から重心の座標を計算します。
その重心周りに図形を回転させるだけです。
Tkinterで図形を回転させるプログラムは、下記をご覧ください。
>> 【Tkinter】図形を回転させる!自動で回転・ドラッグで回転
まとめ
今回は、図形の重心を求める方法・プログラムをご紹介しました。
自己交差のない図形であれば、次の手順で重心の位置がわかるのでしたね。
最後までお付き合いいただき、ありがとうございました。