3点の座標から角度と回転方向を求める方法を解説！プログラムで自動化！

3点の座標から角度・回転方向を求めるプログラム

SHARE

この記事の内容

  • \(3\)点の座標から角度を求める方法
  • \(3\)点の座標から回転方向を求める方法
  • 角度と回転方向を求めるプログラム

こんにちは、Youta(@youta_blog)です。

今回は、座標平面上の\(3\)点の座標から角度と回転方向を求めるお話です。

あなたは学生時代、次のような問題を見たことはありますか？

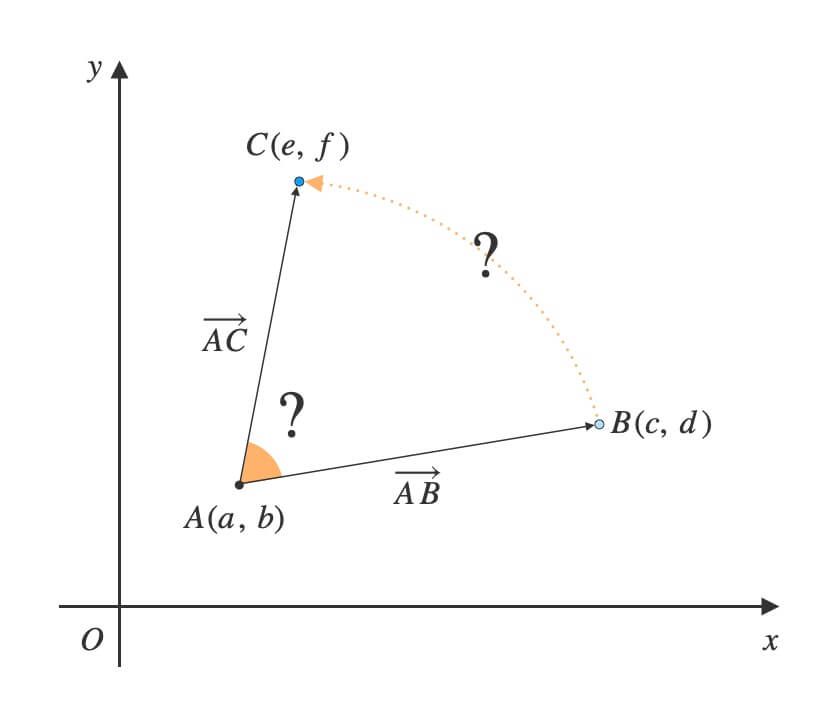
3点の座標から角度と回転方向を求める問題

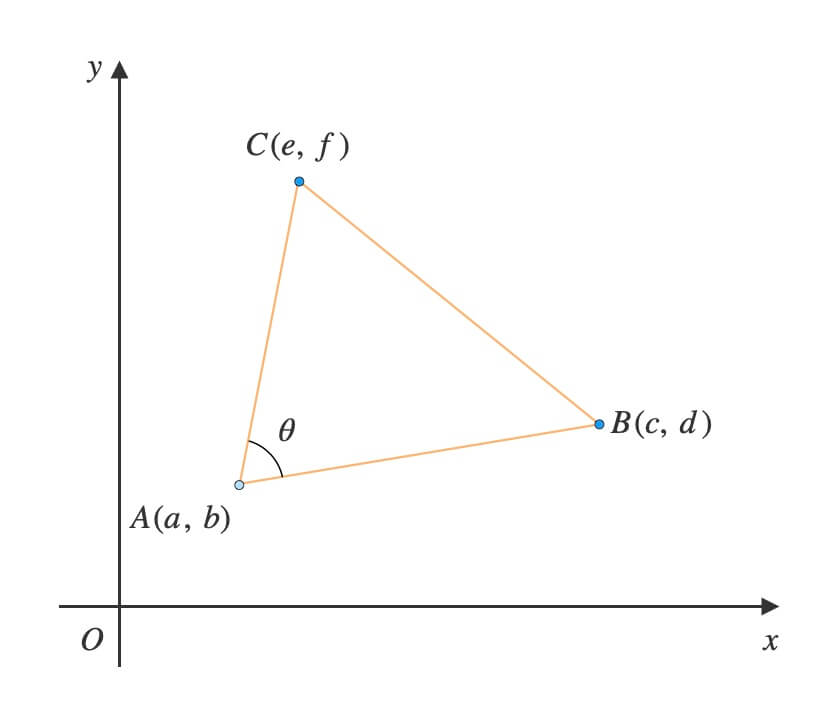
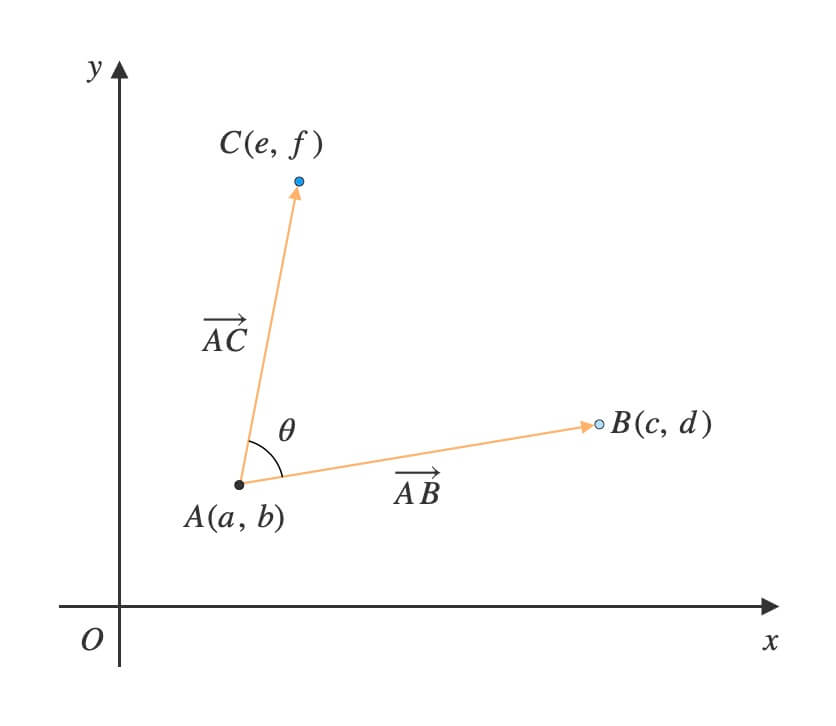
座標平面内に\(3\)点\(A(a,\ b)\), \(B(c,\ d)\), \(C(e,\ f)\) がある。

ただし、\(A\ne B\ne C\)とする。

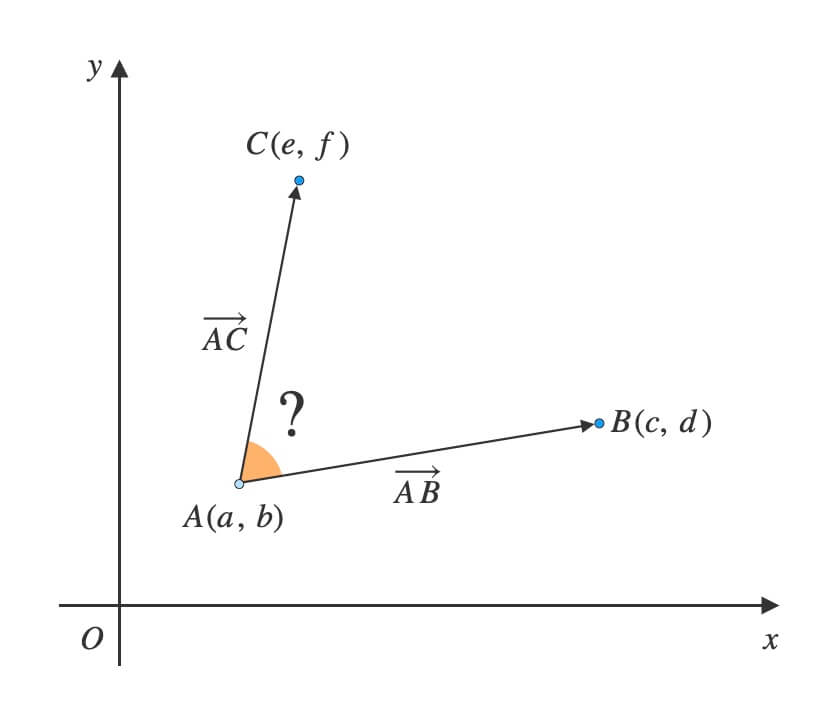
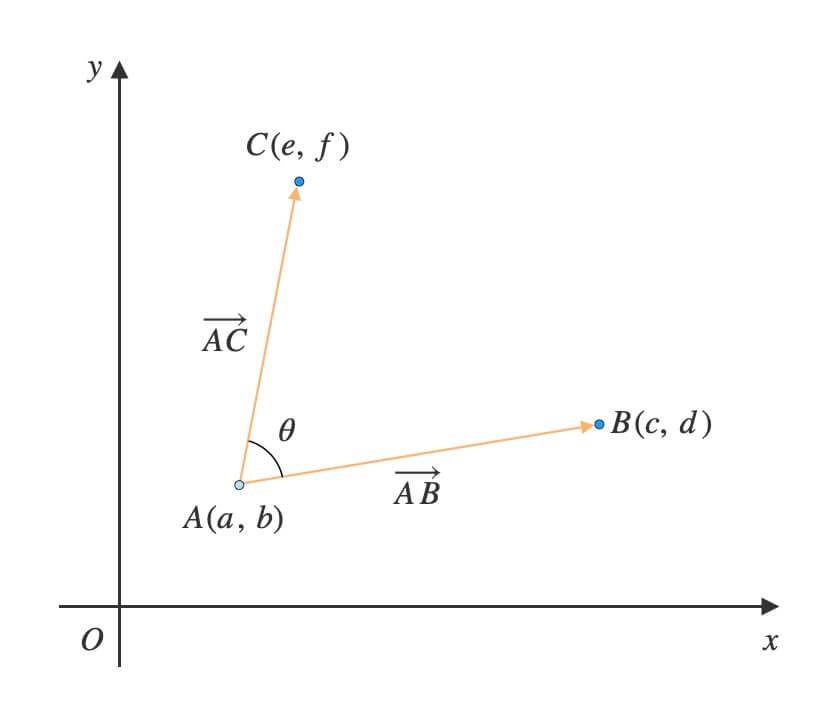
(1) ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)のなす角\(\theta\)を求めよ。

(2) ベクトル\(\overrightarrow{AB}\)に対して\(\overrightarrow{AC}\)は時計回りか反時計回りかを判別せよ。

解法を忘れてしまったり、そもそもどう解けばいいかわからない…という方が多いのではないでしょうか。

でもご安心ください！

記事を読めば、この問題の対処法を学べます。

合わせて、コンピュータに自動で解かせるためのプログラムもご紹介します。

3点から角度を求める2つの方法

まずは冒頭の問題の\((1)\)の答えを示します。

3点の座標から角度を求める問題

答え

\(\theta = \arccos{\frac{(c-a)(e-a) + (d-b)(f-b)}{\sqrt{{(c-a)}^2 + {(d-b)}^2}\sqrt{{(e-a)}^2 + {(f-b)}^2}}}\)

すずか

意味わからん。
大丈夫です。こうなる理由を\(2\)通りの方法で解説しますね。

先生

ベクトルの内積を使うやり方

手順は簡単。たった\(5\)ステップです。

  1. ベクトルを作る
  2. ベクトルの大きさを求める
  3. ベクトルの内積を求める
  4. 角度の余弦を求める
  5. 逆余弦関数で角度を求める

\(1\)ステップずつ丁寧に解説しますね。

 ベクトルを作る

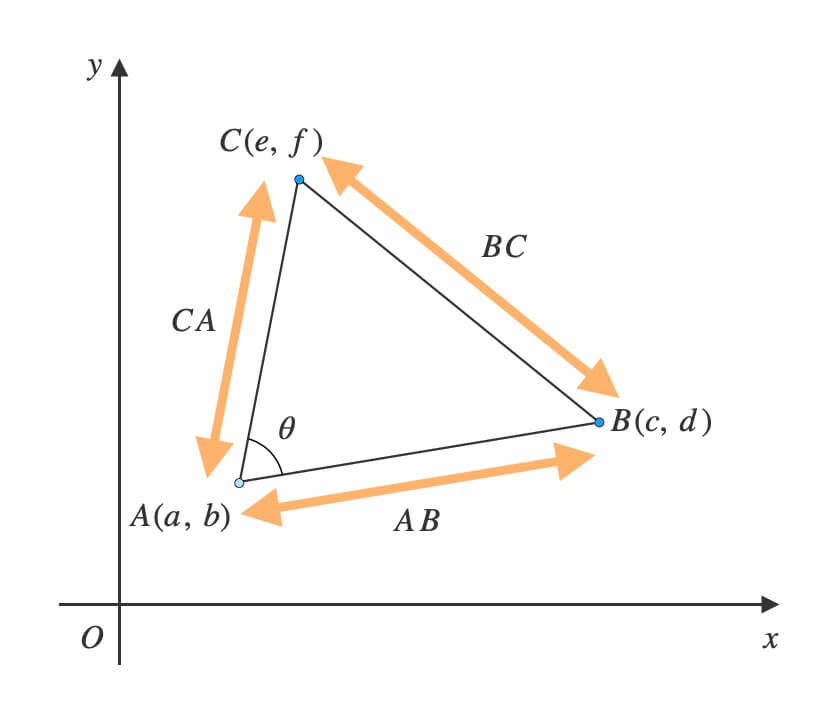
3点の座標からベクトルを作る

\(A\)を始点、\(B\)と\(C\)は終点とします。

このときベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)ができます。

\(A\), \(B\), \(C\)の各座標が分かっているので、ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示が可能です。

ベクトルの成分表示

\(A = (a_1,\ a_2)\)かつ\(B = (b_1,\ b_2)\) \(\Rightarrow \overrightarrow{AB} = (b_1 – a_1,\ b_2 – a_1)\)

各ベクトルの成分表示は次のようになります。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示

  • \(\overrightarrow{AB}=(c-a,\ d-b)\)
  • \(\overrightarrow{AC}=(e-a,\ f-b)\)

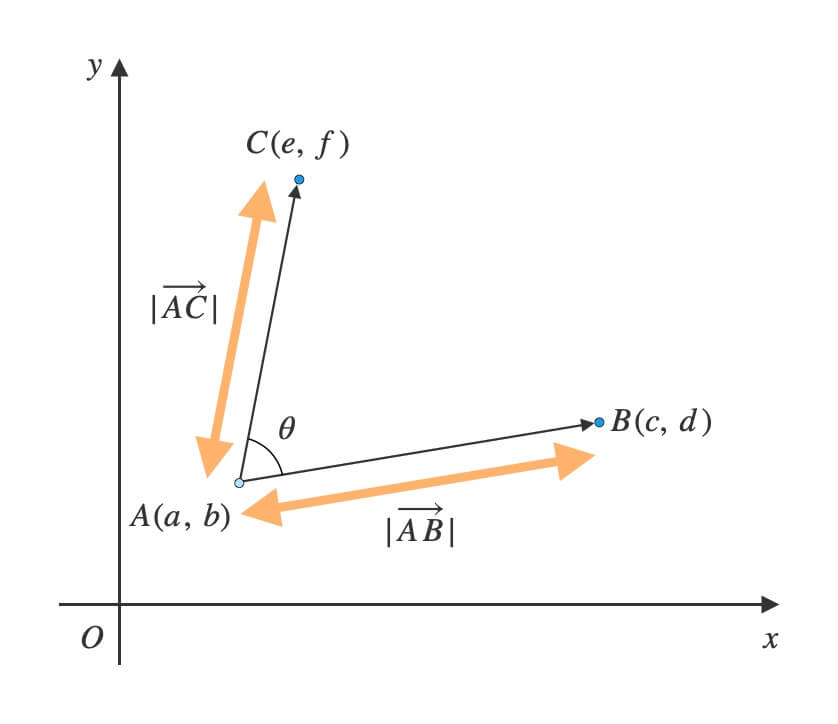
 ベクトルの大きさを求める

ベクトルの大きさを求める

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の大きさを求めます。

成分表示からベクトルの大きさを求めるには、次の公式を利用します。

ベクトルの大きさ

\(\overrightarrow{a}=(a_1,\ a_2)\) \(\Rightarrow |\overrightarrow{a}| =\sqrt{a_1^2 + a_2^2} \)

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示を既に求めてあるので、公式に当てはめて計算です。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の大きさ

  • \(|\overrightarrow{AB}| = \sqrt{{(c-a)}^2 + {(d-b)}^2}\)
  • \(|\overrightarrow{AC}| = \sqrt{{(e-a)}^2 + {(f-b)}^2}\)

 ベクトルの内積を求める

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の内積を求めます。

ベクトルの内積を求めるには、\(2\)通りの方法があります。

内積の公式
  1. \(\overrightarrow{a}=(a_1,\ a_2)\)かつ\(\overrightarrow{b}=(b_1,\ b_2)\) \(\Rightarrow \overrightarrow{a} \cdot \overrightarrow{b} = a_1b_1 + a_2b_2\)
  2. \(\overrightarrow{a}\)と\(\overrightarrow{b}\)のなす角が\(\theta\) \(\Rightarrow \overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}| |\overrightarrow{b}|\cos{\theta}\)

\(1\)の公式に、ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示を当てはめましょう。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の内積

\(\overrightarrow{AB} \cdot \overrightarrow{AC} = (c-a)(e-a) + (d-b)(f-b)\)

 角度の余弦を求める

\(\cos{\theta}\)を求めます。

内積の公式\(2\)より\(\overrightarrow{AB} \cdot \overrightarrow{AC} = |\overrightarrow{AB}| |\overrightarrow{AC}|\cos{\theta}\)とも表せました。

これを変形すると\(\cos{\theta} = \frac{\overrightarrow{AB} \cdot \overrightarrow{AC}}{|\overrightarrow{AB}| |\overrightarrow{AC}|}\)ですね。

\(\overrightarrow{AB} \ne \overrightarrow{0}\)かつ\(\overrightarrow{AC} \ne \overrightarrow{0}\)より、上記の式変形が許されます。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の内積と大きさを代入し、なす角\(\theta\)の余弦を求めます。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)のなす角\(\theta\)の余弦

\(\cos{\theta} = \frac{(c-a)(e-a) + (d – b)(f – b)}{\sqrt{{(c-a)}^2 + {(d-b)}^2}\sqrt{{(e-a)}^2 + {(f-b)}^2}}\)

 逆余弦関数で角度を求める

すずか

知りたいのって\(\theta\)でしょ？

\(\cos{\theta}\)求めても意味なくない？

実は、\(\cos{\theta}\)から\(\theta\)を求められます。

先生

結論、逆余弦関数を使います。

逆余弦関数

\(\cos{\theta} = x \Leftrightarrow \theta = \arccos{x}\)　\((0\le\theta\le\pi)\)

要は、\(\cos{\theta}\)が〇〇になる角度\(\theta\)ってな〜んだ？

この角度\(\theta\)を求めるのが逆余弦関数です。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)のなす角\(\theta\)の余弦は既に求めてあるので、これで\(\theta\)がわかります。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)のなす角\(\theta\)

\(\theta = \arccos{\frac{(c-a)(e-a) + (d – b)(f – b)}{\sqrt{{(c-a)}^2 + {(d-b)}^2}\sqrt{{(e-a)}^2 + {(f-b)}^2}}}\)

お疲れ様でした。

以上が、ベクトルの内積を利用して\(3\)点の座標から角度を導出する流れです。

先ほどの答えと一致していますね。

余弦定理を使うやり方

手順は簡単。たった\(5\)ステップです。

  1. 三角形を作る
  2. 三角形の辺の長さを求める
  3. 三角形に余弦定理を適用する
  4. 角度の余弦を求める
  5. 逆余弦関数で角度を求める

\(1\)ステップずつ丁寧に解説しますね。

 三角形を作る

3点の座標から三角形を作る

\(A\), \(B\), \(C\)を頂点とする三角形を作ります。

 三角形の辺の長さを求める

三角形の各辺の長さを求める

辺\(AB\), \(BC\), \(CA\)の長さを求めます。

座標平面上の\(2\)点間の距離を求めるには、次の公式を利用します。

(2)点間の距離の公式

\(A=(a_1,\ a_2)\)かつ\(B=(b_1,\ b_2)\) \(\Rightarrow AB = \sqrt{{(a_1 – b_1)}^2 + {(a_2 – b_2)}^2}\)

よって、各辺の長さが求まります。

\(\triangle{ABC}\)の各辺の長さ

  • \(AB = \sqrt{{(a – c)}^2 + {(b – d)}^2}\)
  • \(BC = \sqrt{{(c – e)}^2 + {(d – f)}^2}\)
  • \(CA = \sqrt{{(e – a)}^2 + {(f – b)}^2}\)

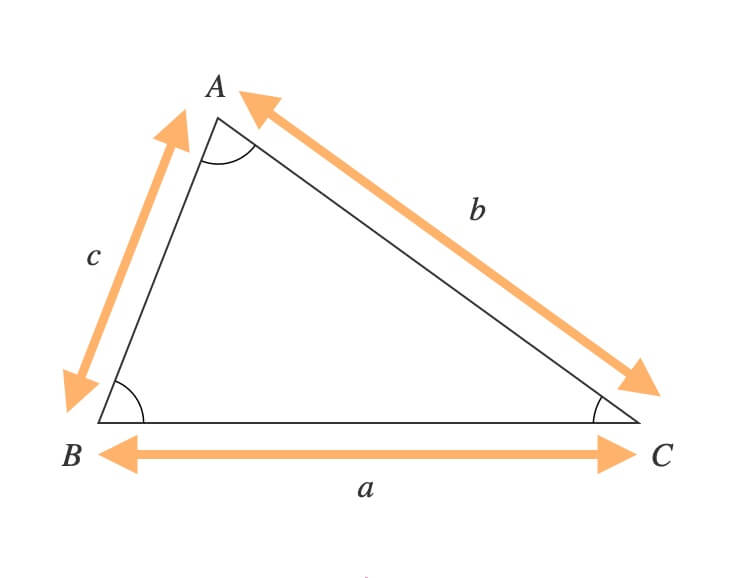
 三角形に余弦定理を適用する

余弦定理

三角形ABC

\(\triangle{ABC}\)について次が成り立つ。

\(a^2 = b^2 + c^2 – 2bc\cos{\angle{A}}\)

\(b^2 = c^2 + a^2 – 2ca\cos{\angle{B}}\)

\(c^2 = a^2 + b^2 – 2ab\cos{\angle{C}}\)

よって、\(\triangle{ABC}\)の各辺と\(\angle{A}\)に関して下記の等式が成り立ちます。

\(\triangle{ABC}\)の各辺と\(\angle{A}\) \((= \theta)\)の関係

\({BC}^2 = {AB}^2 + {CA}^2 – 2 \cdot AB \cdot CA \cdot \cos{\theta}\)

 角度の余弦を求める

\(\cos{\theta}\)を求めます。

\(\triangle{ABC}\)の各辺と\(\theta\)の関係式を変形すると\(\cos{\theta} = \frac{{AB}^2 + {CA}^2 – {BC}^2}{2 \cdot AB \cdot CA}\)ですね。

\(\triangle{ABC}\)の各辺の大きさを代入し、\(\angle{A}\)\(( = \theta)\)の余弦を求めます。

\(\triangle{ABC}\)の\(\angle{A}\) \((= \theta)\)の余弦

\(\cos{\theta} = \frac{(c-a)(e-a) + (d – b)(f – b)}{\sqrt{{(c-a)}^2 + {(d-b)}^2}\sqrt{{(e-a)}^2 + {(f-b)}^2}}\)

次の\(4\)つの等式から導きます。

  1. \(AB = \sqrt{{(a – c)}^2 + {(b – d)}^2}\)
  2. \(BC = \sqrt{{(c – e)}^2 + {(d – f)}^2}\)
  3. \(CA = \sqrt{{(e – a)}^2 + {(f – b)}^2}\)
  4. \(\cos{\theta} = \frac{{AB}^2 + {CA}^2 – {BC}^2}{2 \cdot AB \cdot CA}\)

④に①・②・③を代入します。

\begin{align*}
\cos{\theta} &= \frac{{AB}^2 + {CA}^2 – {BC}^2}{2 \cdot AB \cdot CA} \\
\\\\
&=\frac{{\{\sqrt{{(a – c)}^2 + {(b – d)}^2}\}}^2 + {\{\sqrt{{(e – a)}^2 + {(f – b)}^2}\}}^2 – {\{\sqrt{{(c – e)}^2 + {(d – f)}^2}\}}^2}{2\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{\{{(a – c)}^2 + {(b – d)}^2\} + \{{(e – a)}^2 + {(f – b)}^2\} – \{{(c – e)}^2 + {(d – f)}^2\}}{2\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{(a^2 – 2ac + c^2) + (b^2 – 2bd + d^2) + (e^2 – 2ea + a^2) + (f^2 – 2fb + b^2) – (c^2 – 2ce + e^2) – (d^2 – 2df + f^2)}{2\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{\{(2a^2 – 2ac – 2ea + 2ce) + (2b^2 – 2bd – 2fb + 2df)\} + (c^2 + d^2 + e^2 + f^2) – (c^2 + d^2 + e^2 + f^2)}{2\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{2\{(a^2 – ac – ea + ce) + (b^2 – bd – fb + df)\}}{2\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{\{a^2 – (c + e)a + ce\} + \{b^2 – (d + f)b + df\}}{\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{(a – c)(a – e) + (b – d)(b – f)}{\sqrt{{(a – c)}^2 + {(b – d)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\\\\
&=\frac{(c – a)(e – a) + (d – b)(f – b)}{\sqrt{{(c – a)}^2 + {(d – b)}^2}\sqrt{{(e – a)}^2 + {(f – b)}^2}} \\
\end{align*}

 逆余弦関数で角度を求める

すずか

あーなんだっけ、\(\cos{\theta}\)から\(\theta\)分かるんだっけ？
そうです。先ほどの内容をよく覚えていますね。

先生

結論、逆余弦関数を使います。

逆余弦関数

\(\cos{\theta} = x \Leftrightarrow \theta = \arccos{x}\)　\((0\le\theta\le\pi)\)

要は、\(\cos{\theta}\)が〇〇になる角度\(\theta\)ってな〜んだ？

この角度\(\theta\)を求めるのが逆余弦関数です。

\(\triangle{ABC}\)の\(\angle{A}\) \((=\theta)\)の余弦は既に求めてあるので、これで\(\theta\)がわかります。

\(\triangle{ABC}\)の\(\angle{A}\) \((= \theta)\)

\(\theta = \arccos{\frac{(c-a)(e-a) + (d – b)(f – b)}{\sqrt{{(c-a)}^2 + {(d-b)}^2}\sqrt{{(e-a)}^2 + {(f-b)}^2}}}\)

計算が少し大変でしたね。

以上が、余弦定理を利用して\(3\)点の座標から角度を導出する流れです。

どちらでも同じ答えが出るのは面白いですね！

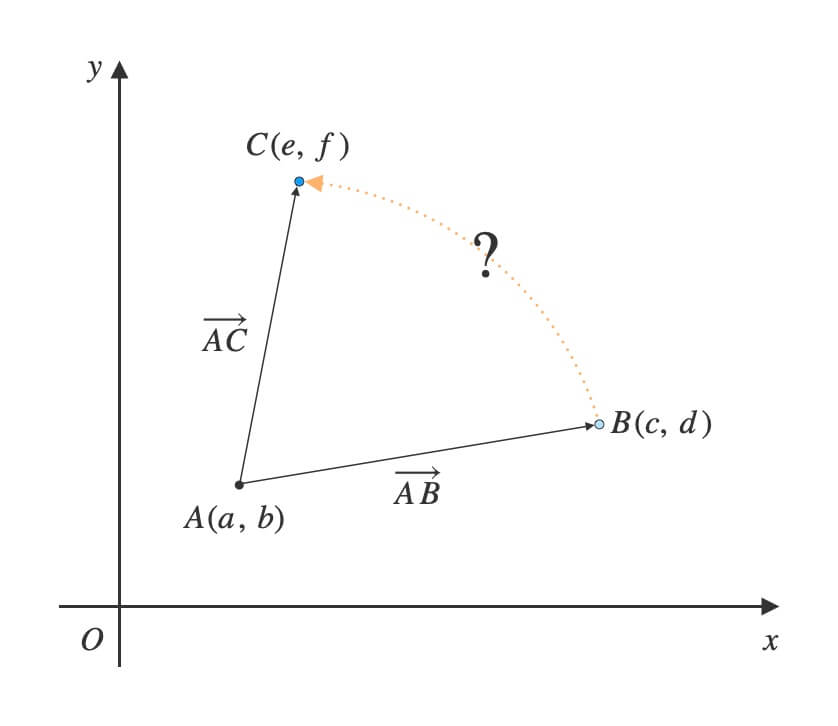
3点から回転方向を求める方法

お次は冒頭の問題の\((2)\)の答えを示します。

3点の座標から回転方向を求める問題

答え

  • \((c-a)(f-b)-(d-b)(e-a)>0\Rightarrow反時計回り\)
  • \((c-a)(f-b)-(d-b)(e-a)<0\Rightarrow時計回り\)
  • \((c-a)(f-b)-(d-b)(e-a)=0\Rightarrow回転なし\)

すずか

また意味不明なのきたわ〜。
丁寧に説明するので安心してくださいね。

先生

結論、ベクトルの外積を利用します。

手順は簡単。たった\(3\)ステップです。

  1. ベクトルを作る
  2. ベクトルの外積を求める
  3. 外積の\(z\)成分で回転方向を判別

\(1\)ステップずつ丁寧に解説しますね。

ベクトルを作る

3点の座標からベクトルを作る

\(A\)を始点、\(B\)と\(C\)は終点とします。

このときベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)ができます。

\(A\), \(B\), \(C\)の各座標が分かっているので、ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示が可能です。

ベクトルの成分表示

\(A = (a_1,\ a_2)\)かつ\(B = (b_1,\ b_2)\) \(\Rightarrow \overrightarrow{AB} = (b_1 – a_1,\ b_2 – a_1)\)

各ベクトルの成分表示は次のようになります。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示

  • \(\overrightarrow{AB}=(c-a,\ d-b,\ 0)\)
  • \(\overrightarrow{AC}=(e-a,\ f-b,\ 0)\)

すずか

あれ〜座標の数\(1\)個多くない？
後ほど外積の計算で使うので、\(z\)成分を加えました。

先生

何も難しくはありません。

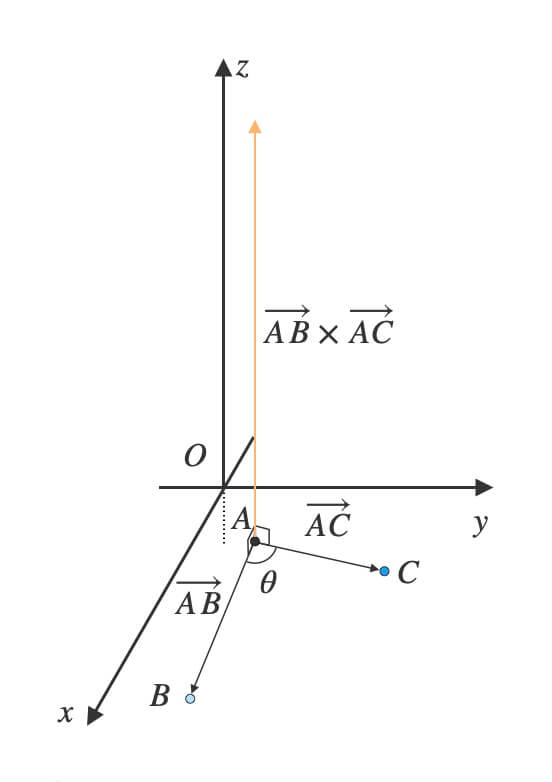
ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)は座標平・面・上にあるので、\(z\)成分は\(0\)ですよね。

ベクトルの外積を求める

ベクトルの外積を求める

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の外積を求めます。

ベクトルの外積を求めるには、次の公式を利用します。

外積の公式

\(\overrightarrow{a}=(a_1,\ a_2, a_3)\)かつ\(\overrightarrow{b}=(b_1,\ b_2, b_3)\) \(\Rightarrow \overrightarrow{a} \times \overrightarrow{b} = (a_2b_3-a_3b_2,\ a_3b_1-a_1b_3,\ a_1b_2-a_2b_1)\)

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の成分表示を既に求めてあるので、公式に当てはめるだけです。

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の外積

\(\overrightarrow{AB} \times \overrightarrow{AC} = (0,\ 0,\ (c-a)(f-b)-(d-b)(e-a))\)

外積の\(z\)成分で回転方向を判別

外積の\(z\)成分の符号で回転方向がわかります。

回転方向には次の\(3\)通りがあります。

  • \(z成分>0\Rightarrow\)反時計回り
  • \(z成分<0\Rightarrow\)時計回り
  • \(z成分=0\Rightarrow\)回転なし

ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)の外積は既に求めてあるため、その\(z\)成分で回転方向を判別します。

ベクトル\(\overrightarrow{AB}\)に対する\(\overrightarrow{AC}\)の回転方向

  • \((c-a)(f-b)-(d-b)(e-a)>0\Rightarrow反時計回り\)
  • \((c-a)(f-b)-(d-b)(e-a)<0\Rightarrow時計回り\)
  • \((c-a)(f-b)-(d-b)(e-a)=0\Rightarrow回転なし\)

以上、\(3\)点から回転方向を求める方法でした。

すずか

当分はもう計算したくないよ…。
よく頑張りましたね。

では、コンピューターにこの計算をお願いしましょう。

先生

プログラムを実装

先ほどの理論を踏まえた上で、Pythonでプログラムを書いてみましょう。

実装例は\(3\)つご用意しました。

ニーズに合わせてお選びください。

角度を求める


import numpy as np


def get_angle(point_a, point_b, reference_point, is_radian=False):
    # 点Aまたは点Bが基準点と同じ場合、角度は0を返す
    if point_a == reference_point or point_b == reference_point:
        return 0

    # ベクトルを計算
    reference_point = np.array(reference_point)
    vector_a = np.array(point_a) - reference_point
    vector_b = np.array(point_b) - reference_point

    # ベクトルの大きさ(長さ)を計算
    magnitude_a = np.linalg.norm(vector_a)
    magnitude_b = np.linalg.norm(vector_b)

    # 内積を計算
    dot_product = np.dot(vector_a, vector_b)

    # 余弦を計算
    cosine = dot_product / (magnitude_a * magnitude_b)

    # 逆余弦関数を計算して角度を取得
    angle = np.arccos(cosine)

    # 弧度法指定ではない場合、角度を度数法に変換
    return angle if is_radian else np.degrees(angle)

get_angle関数は\(3\)点の座標から角度を求めます。

引数は次の\(4\)つです。

  • point_a: 点Aの座標(リスト or タプル)
  • point_b: 点Bの座標(リスト or タプル)
  • reference_point: 基準点の座標(リスト or タプル)
  • is_radian: Trueだと角度を弧度法で、False(デフォルト)だと度数法で返す。

戻り値は角度です。

  • angle:  角度。引数is_radianで単位を指定。

回転方向を求める


import numpy as np


def get_rotation_direction(from_point, to_point, reference_point):
    # 始点または終点が基準点と同じ場合、回転方向は定義しない
    if from_point == reference_point or to_point == reference_point:
        return 'undefined'

    # 始点と終点からベクトルを計算
    reference_point = np.array(reference_point)
    from_vector = np.array(from_point) - reference_point
    to_vector = np.array(to_point) - reference_point

    # 外積を計算
    cross_product = np.cross(from_vector, to_vector)

    # 外積の符号に応じて角度を調整
    return 'anti-clockwise' if cross_product >= 0 else 'clockwise'

get_rotation_direction関数は\(3\)点の座標から回転方向を求めます。

引数は次の\(3\)つです。

  • from_point: 回転の始点の座標(リスト or タプル)
  • to_point: 回転の終点の座標(リスト or タプル)
  • reference_point: 回転の中心点の座標(リスト or タプル)

戻り値は文字列です。

  • 'clockwise': 時計回り。\(0^{\circ}\)回転も含む。
  • 'anti-clockwise': 反時計回り。
  • 'undefined': 回転を考えない。

\(3\)次元座標空間上の点には対応しておりませんのでご注意ください。

角度と回転方向を求める

def get_signed_angle(from_point, to_point, reference_point, is_radian=False):
    angle = get_angle(from_point, to_point, reference_point, is_radian)
    rotation_direction = get_rotation_direction(from_point, to_point, reference_point)

    return angle if rotation_direction == 'anti-clockwise' else -angle

get_signed_angle関数は角度と回転方向を求めます。

回転方向は、戻り値の符号で判断できます。

引数は次の\(4\)つです。

  • from_point: 回転の始点の座標(リスト or タプル)
  • to_point: 回転の終点の座標(リスト or タプル)
  • reference_point: 回転の中心点の座標(リスト or タプル)
  • is_radian: Trueだと角度を弧度法で、False(デフォルト)だと度数法で返す。

戻り値は角度です。

  • angle: 角度。\(0\)以上で時計回り、\(0\)未満で半時計回り。

\(3\)次元座標空間上の点には対応しておりませんのでご注意ください。

プログラムの試験

角度を求める

\(3\)点の座標から角度を求めるget_angle関数のテストを行います。

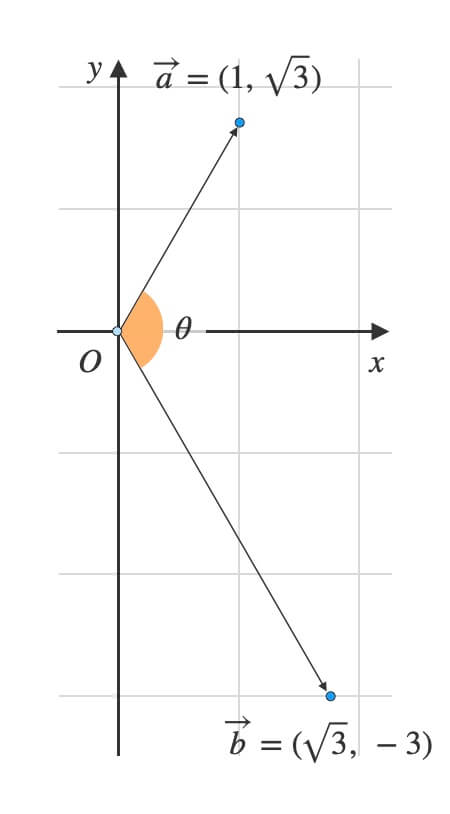
 座標平面上の\(3\)点

ベクトルのなす角を求める問題

ベクトル\(\overrightarrow{a} = (1,\ \sqrt{3})\)と\(\overrightarrow{b}=(\sqrt{3},\ -3)\)のなす角\(\theta\)を求めよ。

5分で解ける！ベクトルのなす角の計算に関する問題から抜粋

答え

\(\theta = 120^{\circ}\)

get_angle関数の下に、次のコード書いて実行します。

a = (1, np.sqrt(3))
b = (np.sqrt(3), -3)
o = (0, 0)

answer = get_angle(a, b, o)

print(answer)

実行結果です。

print(answer)
# 120.00000000000001
誤差はあれど、いい精度ですね。

先生

 座標空間上の\(3\)点

空間の\(3\)点\(A(1,\ −2,\ 3)\), \(B(3,\ −4,\ 2)\), \(C(−3,\ 3,\ 0)\)に対して，ベクトル\(\overrightarrow{AB}\)と\(\overrightarrow{AC}\)のなす角を求めよ。

[05 福井県立大]

答え

\(135^{\circ}\)

get_angle関数の下に、次のコード書いて実行します。

A = (1, -2, 3)
B = (3, -4, 2)
C = (-3, 3, 0)

answer = get_angle(B, C, A)

print(answer)

実行結果です。

print(answer)
# 135.0

回転方向を求める

先ほどの問題を流用します。

ベクトル\(\overrightarrow{a} = (1,\ \sqrt{3})\)に対して\(\overrightarrow{b} = (\sqrt{3},\ -3)\)はどちら回りの回転か。

[5分で解ける！ベクトルのなす角の計算に関する問題 改題]

答え

時計回り

get_rotation_direction関数の下に、次のコード書いて実行します。

a = (1, np.sqrt(3))
b = (np.sqrt(3), -3)
o = (0, 0)

answer = get_rotation_direction(a, b, o)

print(answer)

実行結果です。

print(answer)
# clockwise

角度と回転方向を求める

先ほどの問題を流用します。

ベクトル\(\overrightarrow{a} = (1,\ \sqrt{3})\)に対して\(\overrightarrow{b} =(\sqrt{3},\ -3)\)は反時計回りに何度回転しているか。

[5分で解ける！ベクトルのなす角の計算に関する問題 改題]

答え

\(-120^{\circ}\)

すずか

反時計回りに\(-120^{\circ}\)ってどういうこと？
時計回りに\(120^{\circ}\)という意味です。

先生

get_signed_angle関数の下に、次のコード書いて実行します。

a = (1, np.sqrt(3))
b = (np.sqrt(3), -3)
o = (0, 0)

answer = get_rotation_direction(a, b, o)

print(answer)

実行結果です。

print(answer)
# -120.00000000000001

角度と回転方向が同時に求まりました。

プログラムの活用例

図形をマウスドラッグで回転させるプログラムです。

PythonのGUIライブラリであるTkinterで作りました。

複雑そうですが、仕組みはシンプルです。

マウスカーソルの位置が変化するたびに、次の\(3\)点から回転角度を求めています。

  • カーソルの現在位置
  • カーソルの移動前の位置
  • 図形の重心

次に、求めた角度を元に図形の頂点を回転移動させるだけです。

>>任意点周りの回転移動を２通り解説！プログラムで自動化！

現在Tkinter搭載の関数では、図形を回転させることはできません。

しかし、今回ご紹介した点を回転させるプログラムを上手く使うと、このようにクルクル回すことが出来るのです。

Tkinterで図形を回転させるプログラムに関する記事は、近日中に公開します！

まとめ

今回は、\(3\)点の座標から角度と回転方向を求める方法について解説しました。

角度を求める方法は\(2\)通りありましたね。

上記いずれのやり方でも、余弦と逆余弦関数が重要でした。

また、回転方向は外積の\(z\)成分で判別します。

  • \(z成分>0\Rightarrow\)反時計回り
  • \(z成分<0\Rightarrow\)時計回り
  • \(z成分=0\Rightarrow\)回転なし

本記事でご紹介した内容は、特にゲーム制作で用いられる技術です。

自分でPCゲームを作る際には是非参考にしてくださいね。

最後までお付き合いいただき、ありがとうございました。

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA


前の記事

Tkinterで角丸長方形を作る方法のアイキャッチ
【Tkinter】角丸長方形の作り方を解説！角の丸みも変更可能…

次の記事

【Python】図形の重心の求め方！凹多角形・凸多角形に対応！
【Python】図形の重心の求め方！凹多角形・凸多角形に対応！