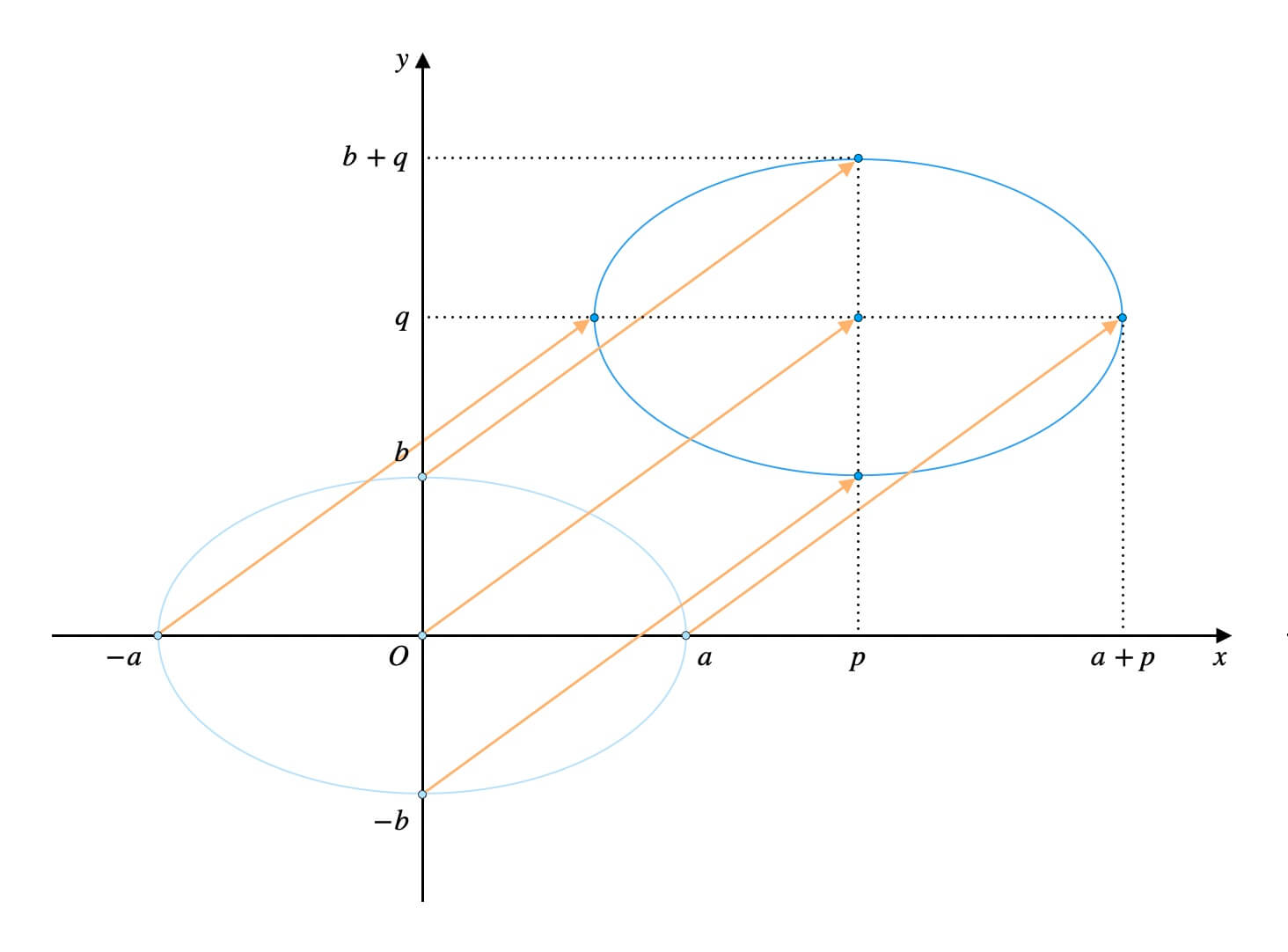この記事の内容
- (楕)円周上の座標を求める方法
- (楕)円周上の座標を求めるプログラム
こんにちは、Youta(@youta_blog)です。
今回は、円や楕円周上の座標を求める方法をお伝えします。
前提として、円は楕円の一種です。
そのため、別個に考えるのではなく楕円一筋で議論を進めます。
楕円周上の任意の座標がわかれば、円周上の座標を求めることなど実に容易いです。
円・楕円周上の座標を求めたい!
円・楕円周上の弧の座標を知りたい!
上記の場合にも対応できるようにします。
理論やプログラムは、より普遍性のある方が美しいのです。
本記事では、解説・確認用コード・実行結果の3点をご用意しております。
また必要に応じてコードの解説をしていますので、初心者でも安心です。
記事の信頼性は、確認用コードと実行結果が保証します。
少しでも疑問に感じたら、是非ともコードをコピペしてPCで確かめてみてください。
さあ、一緒に(楕)円周上の座標を求める旅に出掛けましょう。
Contents
楕円周上の座標を求めるには?
この章では、楕円周上の座標を求めるプロセスを解説していきます。
 すずか
すずか
 先生
先生
結論、楕円の媒介変数表示を利用します。
手順は簡単。たった2ステップです。
なお、今回は楕円の回転は考慮しません。
楕円の回転も加味するのであれば、次のステップで回転後の楕円周上の座標を得られます。
- 回転前の楕円周上の座標を求める。
- 求めた座標を重心周りに回転させる。
ステップ1は、本記事を読み進めてください。
ステップ2は、以前作った任意の点周りに座標を回転させるプログラムをご利用ください。
それでは早速見ていきましょう。
原点中心の楕円周上の座標を取得
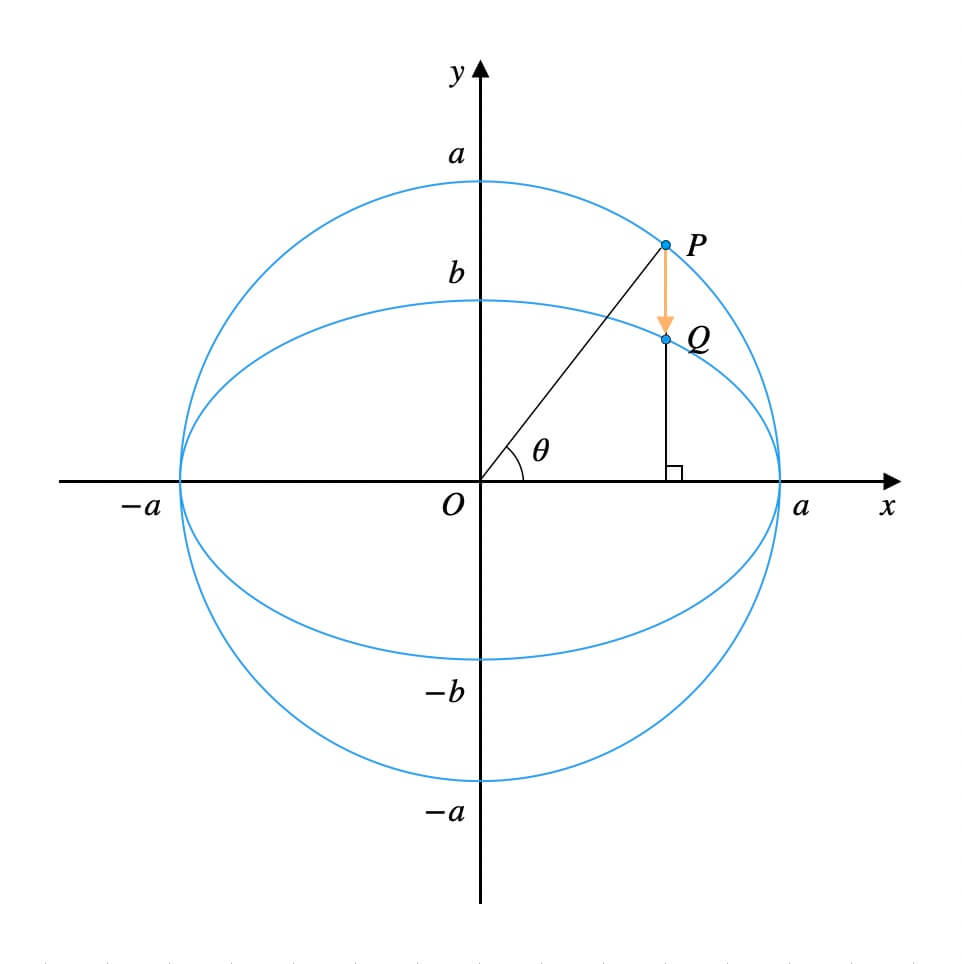
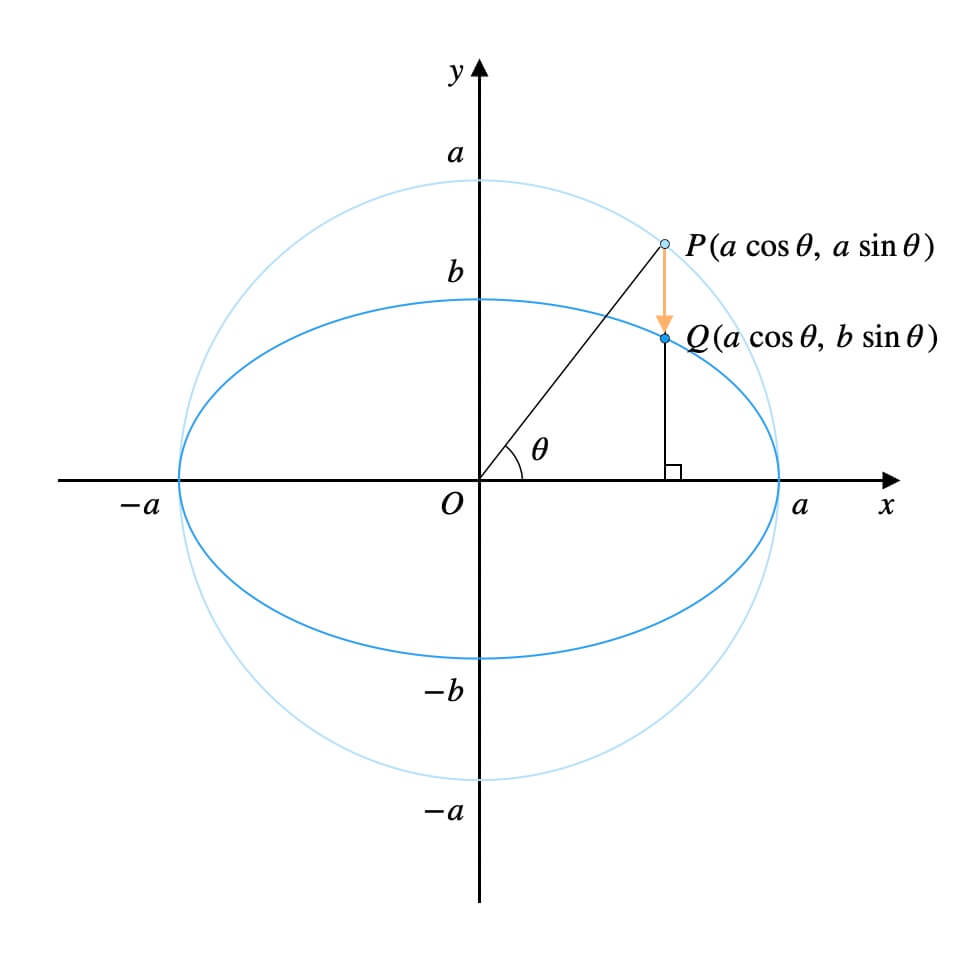
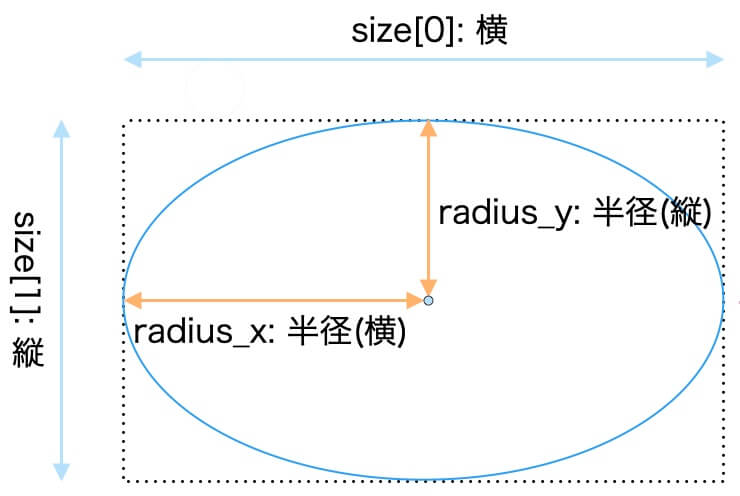
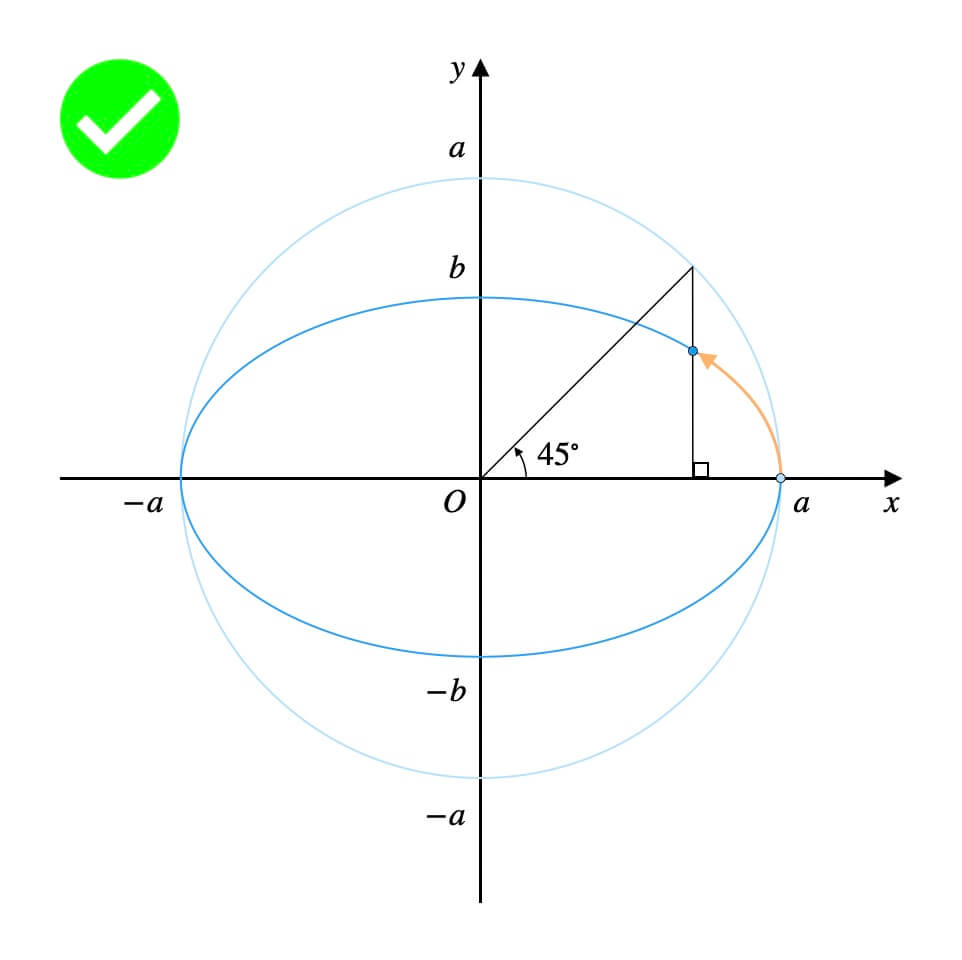
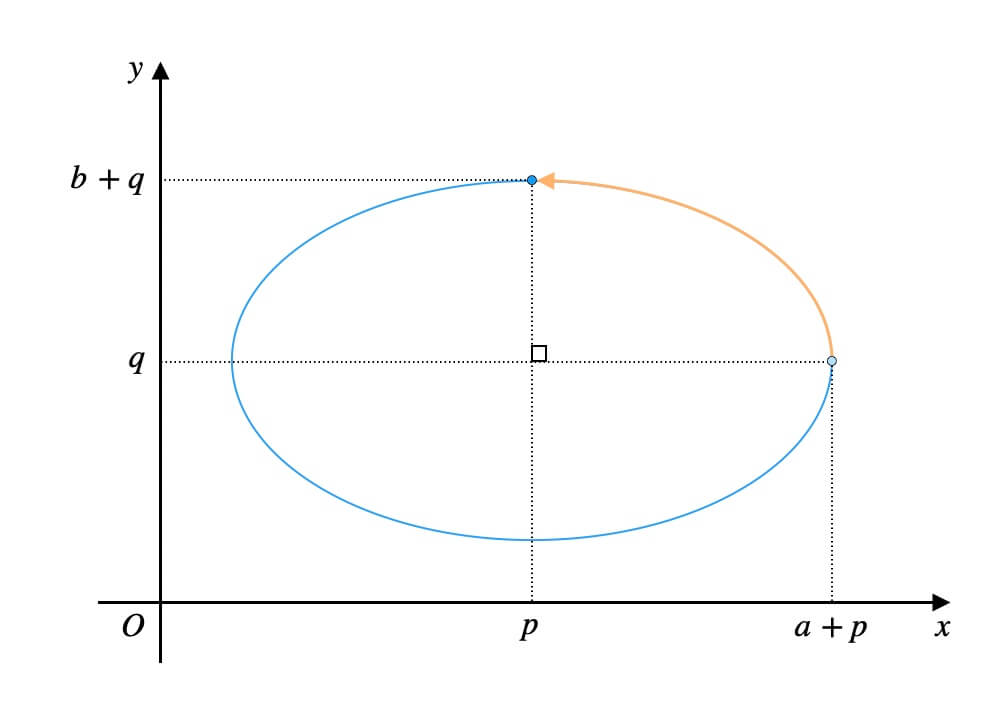
上図を参考に、先にこれから出てくる変数名をまとめます。
- \(a\): 楕円の半径(横)・円の半径
- \(b\): 楕円の半径(縦)
- \(P\): 円上の点
- \(Q\): 円を押し潰した際の\(P\)の移動先
- \(\theta\): 動径\(OP\)の表す一般角
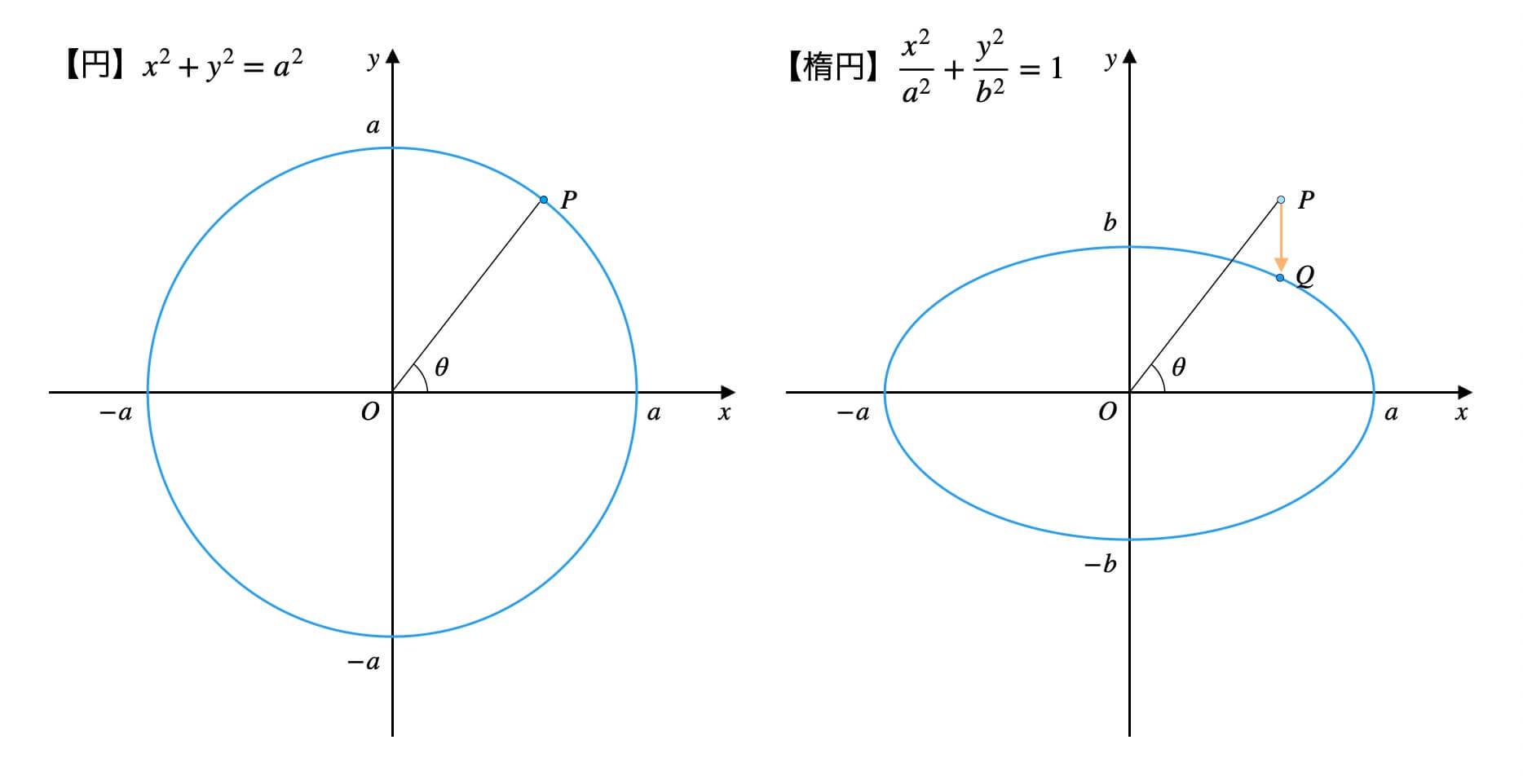
\(xy\)座標平面上に、円と楕円があります。
方程式は\(x^2+y^2=a^2\)と\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)です。
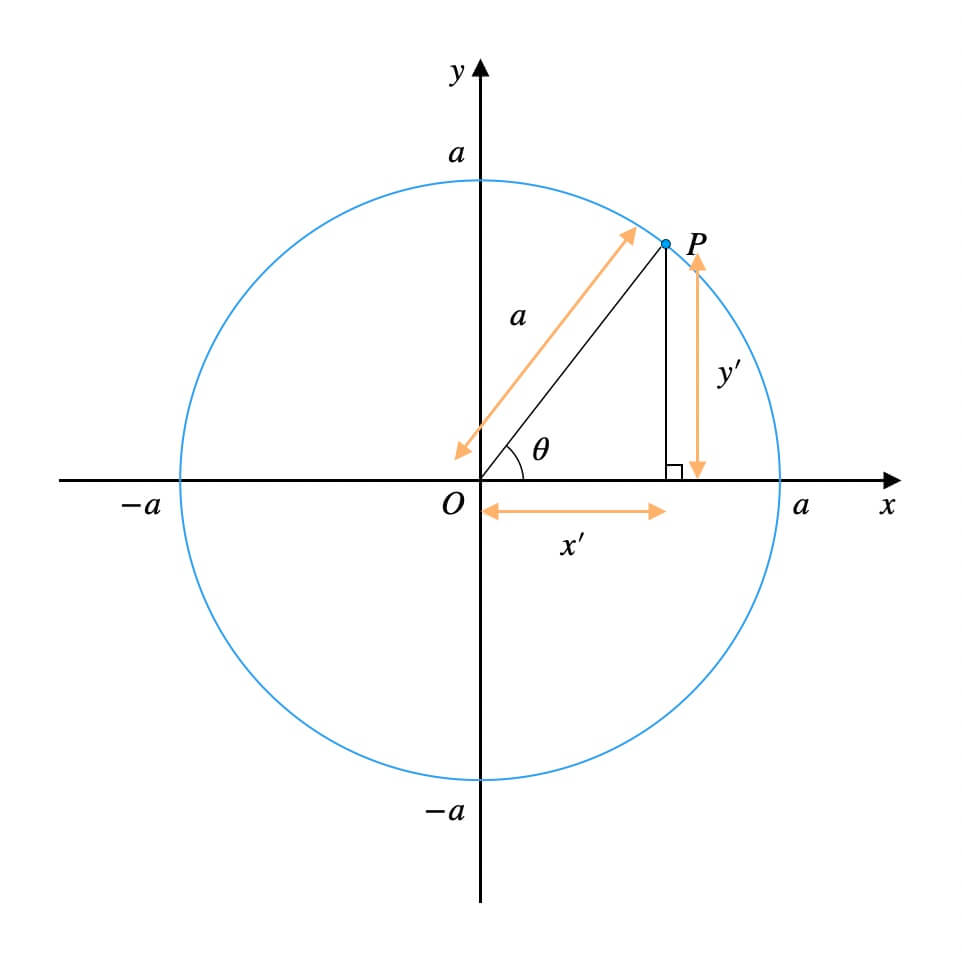
円\(x^2+y^2=a^2\)上の点\(P\)の座標を考えます。
結論、点\(P\)の座標は\((a\cos{\theta}, a\sin{\theta})\)です。
三角関数の定義から導けます。
- \(\cos{\theta}=\frac{x’}{a}\Rightarrow x’=a\cos{\theta}\)
- \(\sin{\theta}=\frac{y’}{a}\Rightarrow y’=a\sin{\theta}\)
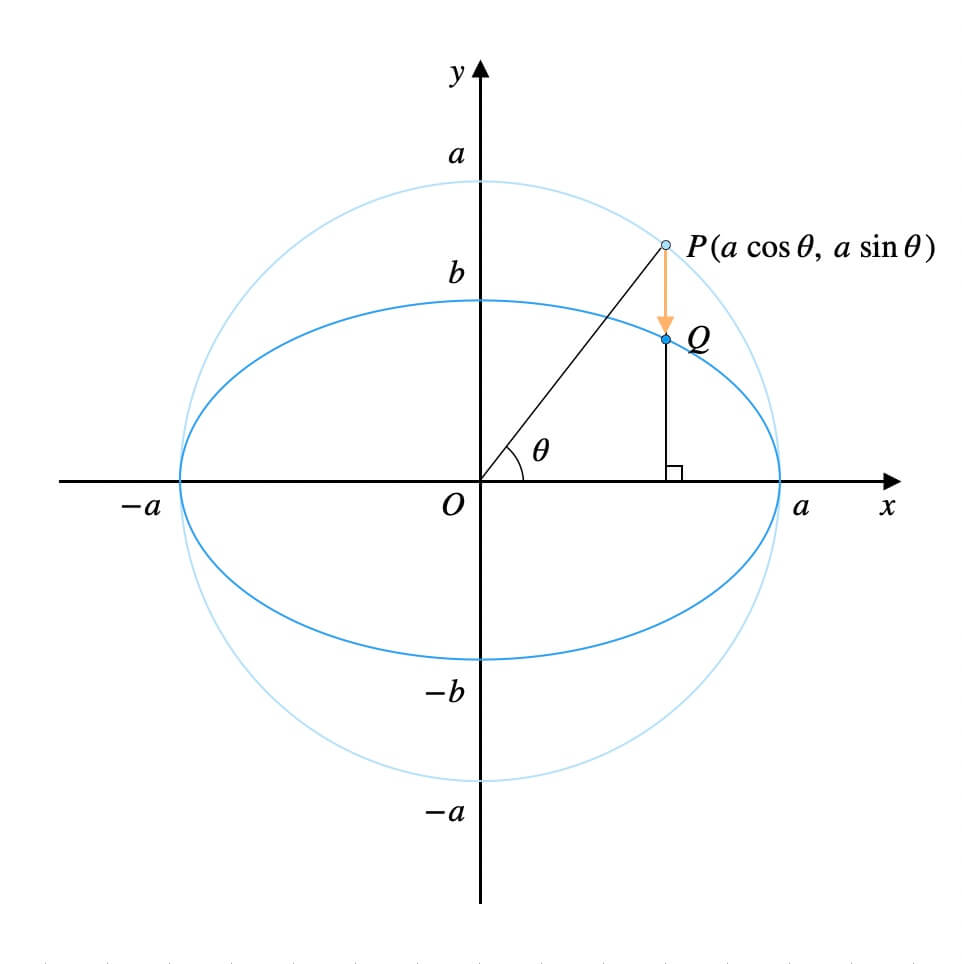
では、楕円\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)上の点\(Q\)の座標はどう考えましょうか。
ここで、次の数学的事実を利用します。
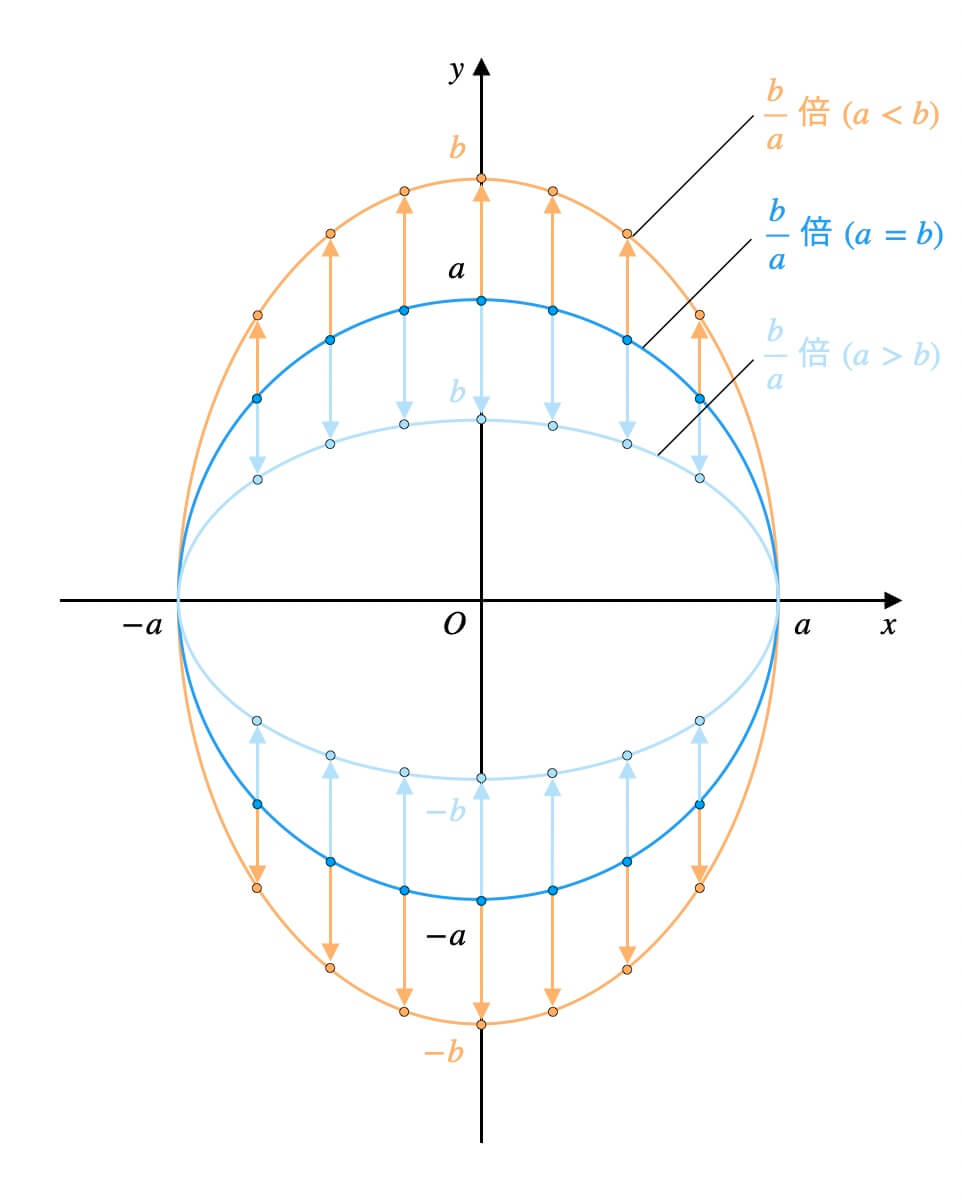
一般に、楕円\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)は、円\(x^2+y^2=a^2\)を、\(x\)軸をもとにして\(y\)軸方向に\(\frac{b}{a}\)倍して得られる曲線である。
つまり、円を縦に伸縮すると円周上の各点は自身の\(y\)座標を\(\frac{b}{a}\)倍した座標に移動します。
なお、\(x\)座標はそのまま引き継がれます。
つまり、\(Q\)の座標は\((a\cos{\theta}, b\sin{\theta})\)です。
\(Q\)の\(y\)座標は\(P\)の\(y\)座標の\(\frac{b}{a}\)倍ですからね。
以上の計算を\(0^\circ{}\)〜\(360^\circ{}\)の\(\theta\)で行うと、楕円周上の座標をすべて取得できます。
取得した座標を指定の位置に平行移動
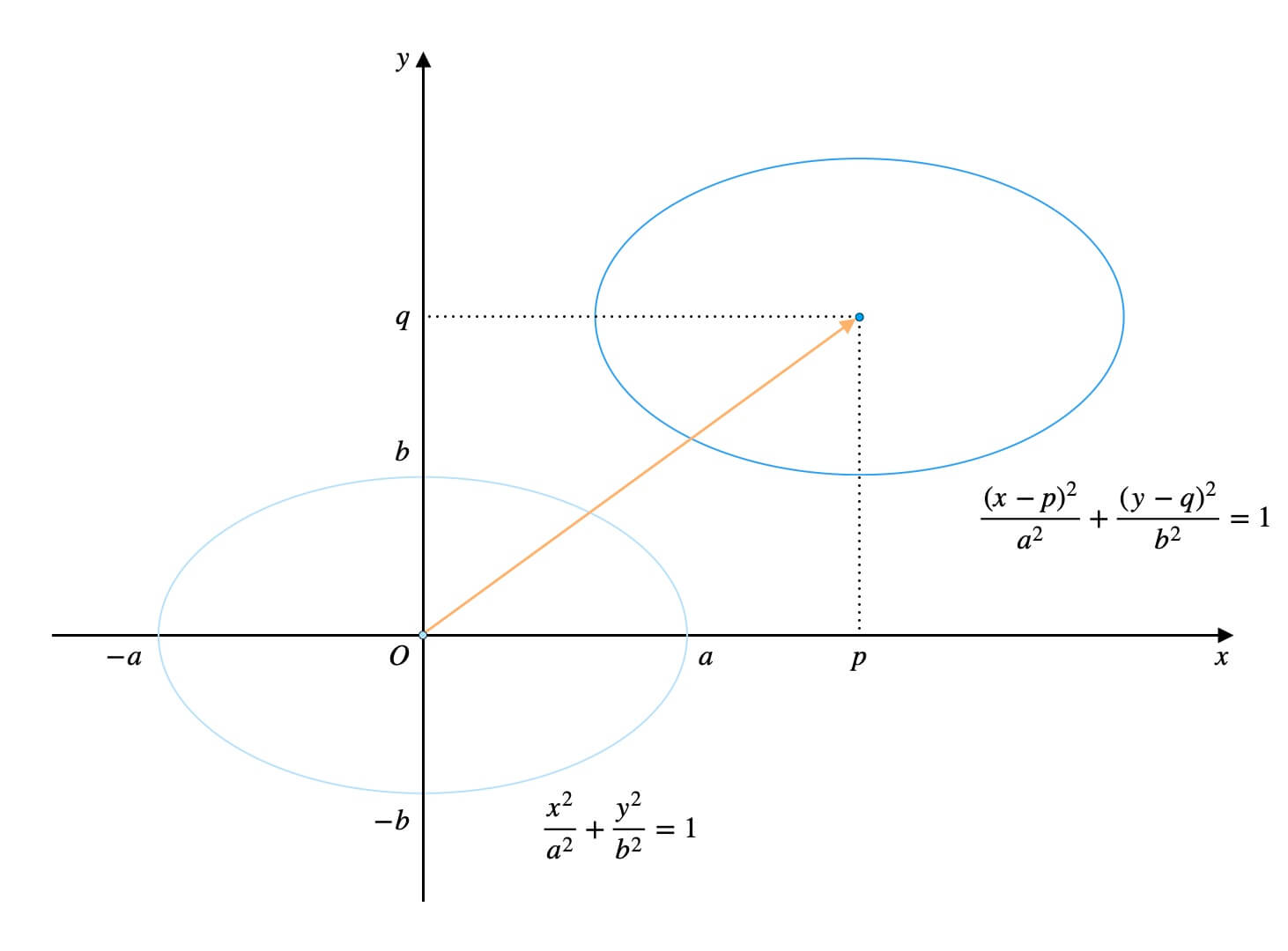
次に、楕円の位置をずらします。
先程のステップだけでは、原点中心の楕円にしか対応できません。
中心がどこにあっても、同様に楕円周上の座標を取れたら嬉しいですよね。
では、具体例を見ていきましょう。
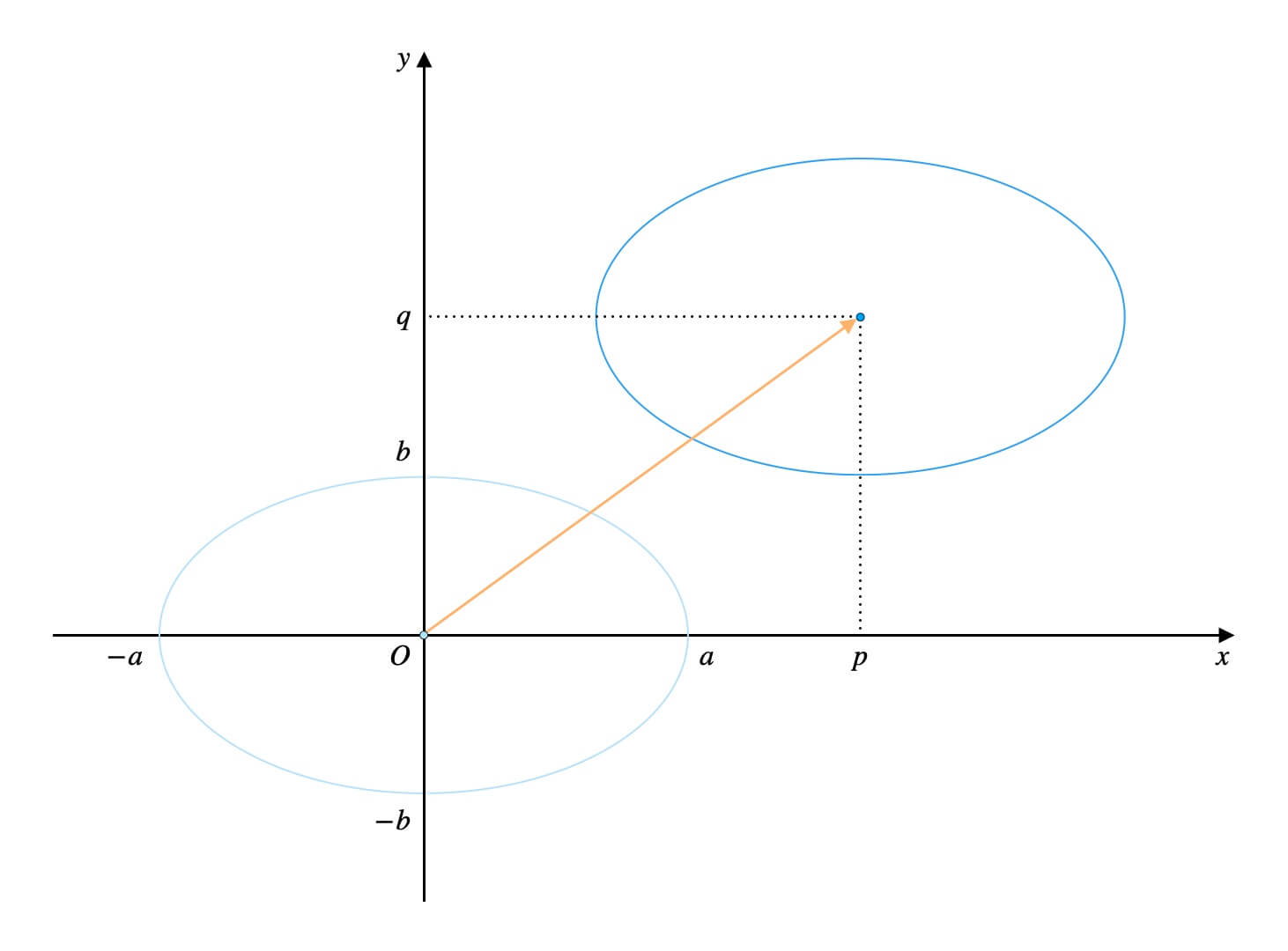
中心を座標\((p, q)\)に重ねるように、楕円全体を平行移動させます。
移動量は、\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)です。
このとき、楕円周上の各点も\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ動きます。
楕円周上の各点の\(x\)座標に\(p\)を、\(y\)座標に\(q\)を加えればOKです。
これで、楕円の中心が\(xy\)座標平面上のどこにあっても、その楕円周上の座標が取得できます。
楕円周上の座標を求めるプログラム
numpyのインストール
これから実装するプログラムは、Pythonの数値解析ライブラリであるnumpyを使います。
numpyは非常に高速に計算できる関数を提供しますが、デフォルトでは入っていません。
そこで、下記コマンドをターミナルに入力・Enterで、numpyをインストールしましょう。
pip install numpy実装例
実際にプログラムを書いてみましょう。
以下に、楕円周上の座標を求めるプログラムの実装例を示します。
import numpy as np
def get_arc_coords(center, size, angle_range, is_radian=False, num_coords=None):
# 引数から必要な情報を抽出
center_x, center_y = center # 楕円の中心座標
radius_x, radius_y = np.array(size) / 2 # 楕円の縦横の径
start_angle, end_angle = angle_range # 弧の範囲の角度
# 弧の角度単位が度数法の場合、弧度法に変換
if not is_radian:
start_angle = np.radians(start_angle)
end_angle = np.radians(end_angle)
# 座標の数が指定されない場合、角度範囲から自動的に計算
if num_coords is None:
angle_diff_radians = end_angle - start_angle # 角度範囲の差分(弧度法)
angle_diff_degrees = np.degrees(angle_diff_radians) # 角度範囲の差分(度数法)
signed_num_coords = int(angle_diff_degrees) # 角度範囲の差分を整数に変換
num_coords = abs(signed_num_coords) # 座標の数を計算
# 指定された座標数で角度を均等に分割
angle = np.linspace(start_angle, end_angle, num_coords)
# 楕円周上の座標を計算
xs = radius_x * np.cos(angle) + center_x
ys = radius_y * np.sin(angle) + center_y
# 座標を一次元のリストにまとめる
points = []
for x, y in zip(xs, ys):
points.extend((x, y))
# 計算された座標のリストを返す
return points
上記の関数は、楕円の位置とサイズ・弧の範囲を指定すると、楕円周上の指定の範囲の弧の座標を返します。
引数は次の5つです。
- center: 楕円の中心座標のタプル
- size: 楕円のサイズ(横\(×\)縦)のタプル
- angle_range: 弧の範囲の角度のタプル
- is_radian: 度数法か弧度法かを示すブール。デフォルトはFalse。
- num_coords: 座標の数の整数。デフォルトはNone。
戻り値は、楕円周上の弧に沿った座標のリストです。
解説
このプログラムの処理は、6つに分けられます。
引数から必要な情報を抽出
ここでは、引数のアンパックを行っています。
center_x, center_y = center
radius_x, radius_y = np.array(size) / 2
start_angle, end_angle = angle_range
アンパックとは、リストやタプルなどを複数の変数に展開して代入することです。
sequence = (1, 2, 3)
a, b, c = sequence
print(a)
print(b)
print(c)
# 1
# 2
# 3
 すずか
すずか
 先生
先生
sizeの要素とradius_x, radius_yの関係です。
この行は、処理を3つ行っています。
radius_x, radius_y = np.array(size) / 2- sizeをnumpy.ndarray型に型変換
- sizeの各要素に\(\frac{1}{2}\)を掛ける
- アンパック
次の処理と同じです。
width, height = size
radius_x, radius_y = width / 2, height / 2
 すずか
すずか
 先生
先生
numpy.ndarray型は要素ごとに演算できます。
a = np.array([1, 2, 3])
print(a)
print(a / 2)
# [1 2 3]
# [0.5 1. 1.5]
もちろんタプルでは不可能です。
a = (1, 2, 3)
# print(a / 2)
# TypeError: unsupported operand type(s) for /: 'tuple' and 'int'弧の角度単位を弧度法に変換
角度が度数法の場合、弧度法に変換します。
if not is_radian:
start_angle = np.radians(start_angle)
end_angle = np.radians(end_angle)
is_radianの真偽と角度の単位の対応関係です。
- True: 弧度法
- False: 度数法(デフォルト)
角度が度数法の場合、is_radianはFalseです。
not FalseでTrueとなり、if文に入ります。
if not is_radian:
if文内部は、度数法のstart_angleとend_angleを共に弧度法に変換する処理です。
start_angle = np.radians(start_angle)
end_angle = np.radians(end_angle)
numpy.radians関数は、度数法を弧度法にします。
a = np.radians(180)
print(a)
# 3.141592653589793度数法の180°は弧度法で\(\pi\)です。
座標の数を角度の範囲から計算
返す座標の個数(num_coords)を指定しない場合、度数法のend_angleとstart_angleの差分が座標数とします。
例えば、start_angleが\(30^\circ{}\)でend_angleが\(60^\circ{}\)ならば、\(60-30\)で\(30\)個の座標を返します。
if num_coords is None:
angle_diff_radians = end_angle - start_angle
angle_diff_degrees = np.degrees(angle_diff_radians)
signed_num_coords = int(angle_diff_degrees)
num_coords = abs(signed_num_coords)
コードでは次の4つの処理を行っています。
最初に、弧度法のend_angleとstart_angleの差を求めます。
弧度法の角度の差なので、変数名はangle_diff_radiansです。
angle_diff_radians = end_angle - start_angle次に、弧度法の角度の差分を度数法にします。
度数法の角度の差分なので、変数名はangle_diff_degreesです。
angle_diff_degrees = np.degrees(angle_diff_radians)
numpy.degrees関数は、弧度法を度数法にします。
a = np.degrees(np.pi)
print(a)
# 180.0弧度法の\(\pi\)は度数法の\(180^\circ{}\)です。
ここで、角度の差分を整数にします。
int関数は小数点以下を切り捨てるので、angle_diff_degreesが7.5であれば7になります。
signed_num_coords = int(angle_diff_degrees)最後に、角度の差分の絶対値を取ります。
num_coords = abs(signed_num_coords)
 すずか
すずか
 先生
先生
例えば、角度の範囲が\(270^\circ{}\)〜\(90^\circ{}\)のとき。
座標数は、\(270-90\)で\(180\)にしたいですよね。
start_angle = 3 / 2 * np.pi # 度数法で270°
end_angle = np.pi / 2 # 度数法で90°
# 範囲の角度(弧度法)の差分を計算
angle_diff_radians = end_angle - start_angle
print(angle_diff_radians)
# -3.141592653589793
# 角度(弧度法)の差分を度数法に変換
angle_diff_degrees = np.degrees(angle_diff_radians)
print(angle_diff_degrees)
# -180.0
# 角度の差分(度数法)をint型に変換
signed_num_coords = int(angle_diff_degrees)
print(signed_num_coords)
# -180
ところが、座標数が\(-180\)となりましたね…。
したがって、絶対値を取ることにより、差分が負でも正しい結果が得られます。
# 角度の差分(度数法)の絶対値を取得
num_coords = abs(int(angle_diff_degrees))
print(num_coords)
# 180この章の処理を、1行でまとめられます。
if num_coords is None:
num_coords = abs(int(np.degrees(end_angle - start_angle)))指定された座標数で角度を均等に分割
角度の範囲をnum_coords等分します。
angle = np.linspace(start_angle, end_angle, num_coords)
numpy.linspace関数は等差数列を作成します。
引数は次の3つを押さえましょう。
- start: 数列の開始値
- end: 数列の終了値
- num: 数列の要素数
本当はもっと引数がありますが、割愛します。
使用例です。
a = np.linspace(0, 6, 3) # 0〜6を3等分
b = np.linspace(10, 0, 6) # 10〜0を6等分
c = np.linspace(0, 1, 11) # 0〜1を11等分
print(a, type(a))
print(b, type(b))
print(c, type(c))
# [0. 3. 6.] <class 'numpy.ndarray'>
# [10. 8. 6. 4. 2. 0.] <class 'numpy.ndarray'>
# [0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ] <class 'numpy.ndarray'>
例えば、\(0\)〜\(6\)ラジアンの範囲で座標を\(3\)個返す場合を見てみましょう。
start_angle = 0
end_angle = 6
num_coords = 3
angle = np.linspace(start_angle, end_angle, num_coords)
print(angle)
# [0. 3. 6.]\(0,\ 3,\ 6\)ラジアンと、範囲が分割されました。
 先生
先生
楕円周上の座標を計算
指定範囲の角度で楕円周上の座標を求めます。
1行目は\(x\)座標、2行目は\(y\)座標の計算です。
xs = radius_x * np.cos(angle) + center_x
ys = radius_y * np.sin(angle) + center_y
難しく見えますが、処理内容は次の2つです。
先ほど、楕円周上の座標を求めるには?で解説しましたね。
こう書けばわかりやすいかと思います。
# 原点中心の楕円周上の座標を取得
xs = radius_x * np.cos(angle)
ys = radius_y * np.sin(angle)
# 取得した座標を指定の位置に平行移動
xs += center_x
yx += center_y
 すずか
すずか
 先生
先生
例えば、関数に次の引数を渡す場合。
- center: \((100, 100)\)
- size: \((400, 200)\)
- angle_range: \((0, 6)\)
- is_radian: True
- num_coords: \(3\)
関数内の値は次のようになりますね。
- center_x: \(100\)
- center_y: \(100\)
- radius_x: \(200\)
- radius_y: \(100\)
- start_angle: \(0\)
- end_angle: \(6\)
- num_coords: \(3\)
\(0\)〜\(6\)ラジアンの範囲で座標を\(3\)個返すため、角度の配列angleは次のようになります。
start_angle = 0
end_angle = 6
num_coords = 3
angle = np.linspace(start_angle, end_angle, num_coords)
print(angle)
# [0. 3. 6.]
では、angleを元に計算を始めます。
まずは原点中心の楕円周上の座標を求めます。
xs = radius_x * np.cos(angle)
ys = radius_y * np.sin(angle)
angleはnumpy.ndarray型なので、angle内の各要素に演算がなされます。
radius_x = 200
angle = [0. 3. 6.]
# 処理
xs = radius_x * np.cos(angle)
# 処理イメージ
xs = [radius_x * np.cos(angle[0]) radius_x * np.cos(angle[1]) radius_x * np.cos(angle[2])]
xs = [200 * np.cos(0.) 200 * np.cos(3.) 200 * np.cos(6.)]
\(y\)座標も同様です。
radius_y = 100
angle = [0. 3. 6.]
# 処理
ys = radius_y * np.sin(angle)
# 処理イメージ
ys = [radius_y * np.sin(angle[0]) radius_y * np.sin(angle[1]) radius_y * np.sin(angle[2])]
ys = [100 * np.sin(0.) 100 * np.sin(3.) 100 * np.sin(6.)]最後に、座標を指定の位置に移動させます。
center_x = 100
xs = [200 * np.cos(0.) 200 * np.cos(3.) 200 * np.cos(6.)]
# 処理
xs += center_x
# 処理イメージ
xs = [200 * np.cos(0.) + 100 200 * np.cos(3.) + 100 200 * np.cos(6.) + 100] center_y = 100
ys = [100 * np.sin(0.) 100 * np.sin(3.) 100 * np.sin(6.)]
# 処理
ys += center_y
# 処理イメージ
ys = [100 * np.sin(0.) + 100 100 * np.sin(3.) + 100 100 * np.sin(6.) + 100]座標を一次元のリストにまとめる
xs内の要素とys内の要素を順に組み合わせて、一次元リストにします。
points = []
for x, y in zip(xs, ys):
points.extend((x, y))
zip関数は複数のリストの要素を一気に取れます。
a = [1, 2, 3]
b = ['a', 'b', 'c']
c = zip(a, b)
print(c)
print(type(c))
print(list(c))
# <zip object at 0x105a60080>
# <class 'zip'>
# [(1, 'a'), (2, 'b'), (3, 'c')]
複数のリストでループを行う際に活躍します。
a = [1, 2, 3]
b = ['a', 'b', 'c']
c = [True, False, None]
for item1, item2, item3 in zip(a, b, c):
print(item1, item2, item3)
# 1 a True
# 2 b False
# 3 c None
for文の処理イメージです。
xs = [x1, x2, x3, ..., xn]
ys = [y1, y2, y3, ..., yn]
points = []
for x, y in zip(xs, ys):
points.extend((x, y))
print(points)
# [x1, y1, x2, y2, x3, y3, ..., xn, yn]要は、\(x\)座標と\(y\)座標を交互に並べるだけです。
最後にpointsを関数外に返して、すべてのプロセスが終了します。
return points弧の範囲の角度について
引数angle_rangeだけは少しクセがあるので、この章で詳細に解説します。
使い方
angle_rangeは、弧の開始角度と終了角度を指定する引数です。
次の2つの値を含むタプルとして、get_arc_coords関数に渡します。
- start_angle: 楕円上の弧の開始位置
- end_angle: 楕円上の弧の終了位置
単位は、度数法 or 弧度法どちらでもOKです。
デフォルトでは度数法ですが、引数 is_radianによって弧度法に切り替えが可能です。
例えば、\(0^\circ{}\)〜\(90^\circ{}\)までの範囲を指定する場合。
# 度数法
get_arc_coords(
(center_x, center_y), # 楕円の中心座標
(width, height), # 楕円のサイズ
(0, 90), # 弧の範囲の角度
)
# 弧度法
get_arc_coords(
(center_x, center_y), # 楕円の中心座標
(width, height), # 楕円のサイズ
(0, np.pi / 2), # 弧の範囲の角度
is_radian=True, # 弧度法モードON
)角度が示す場所に注意
注意点は、角度と弧の範囲の位置関係です。
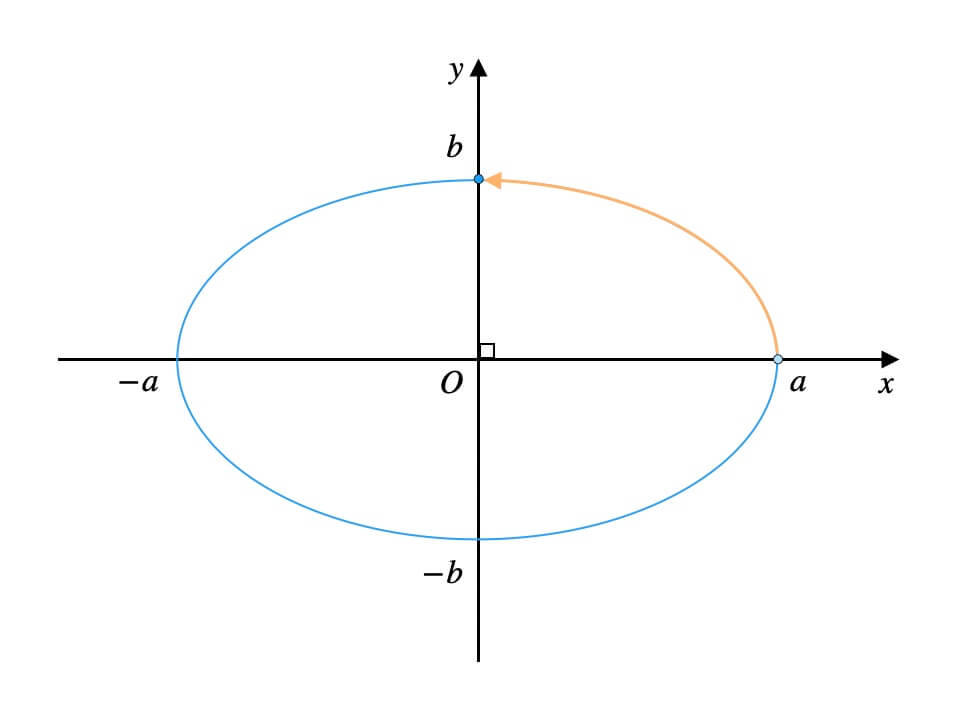
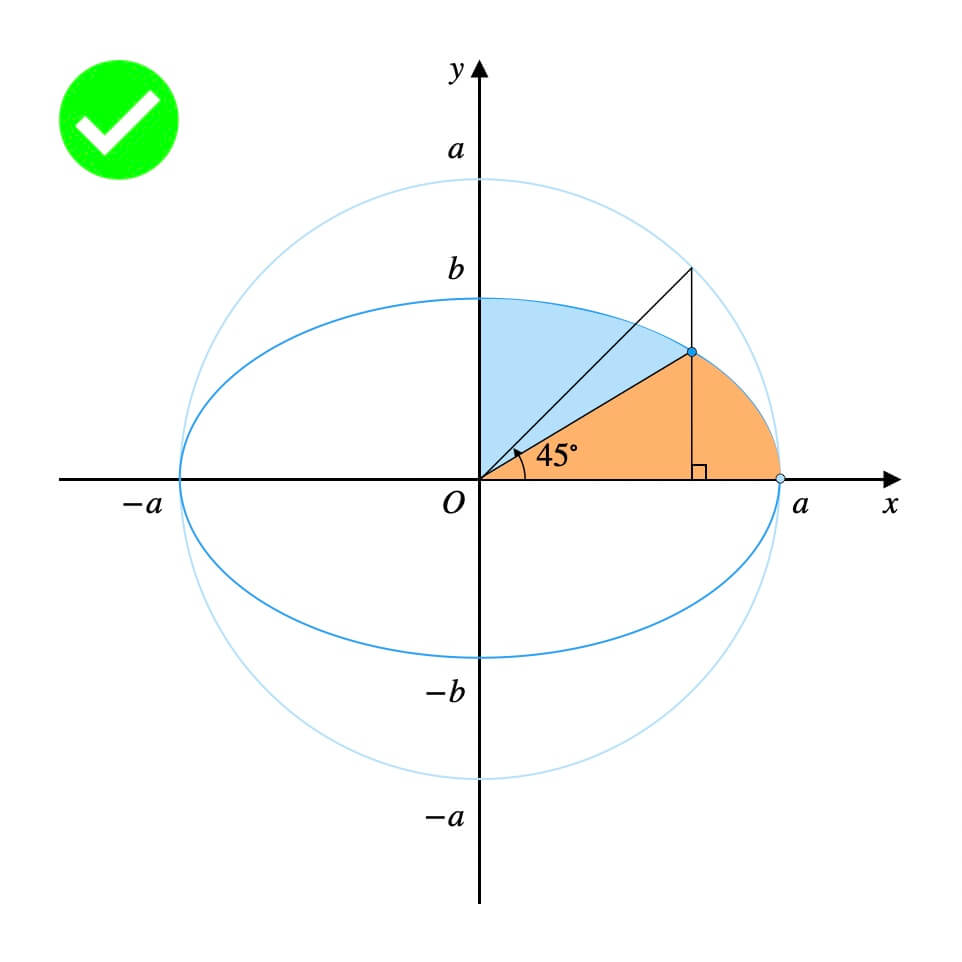
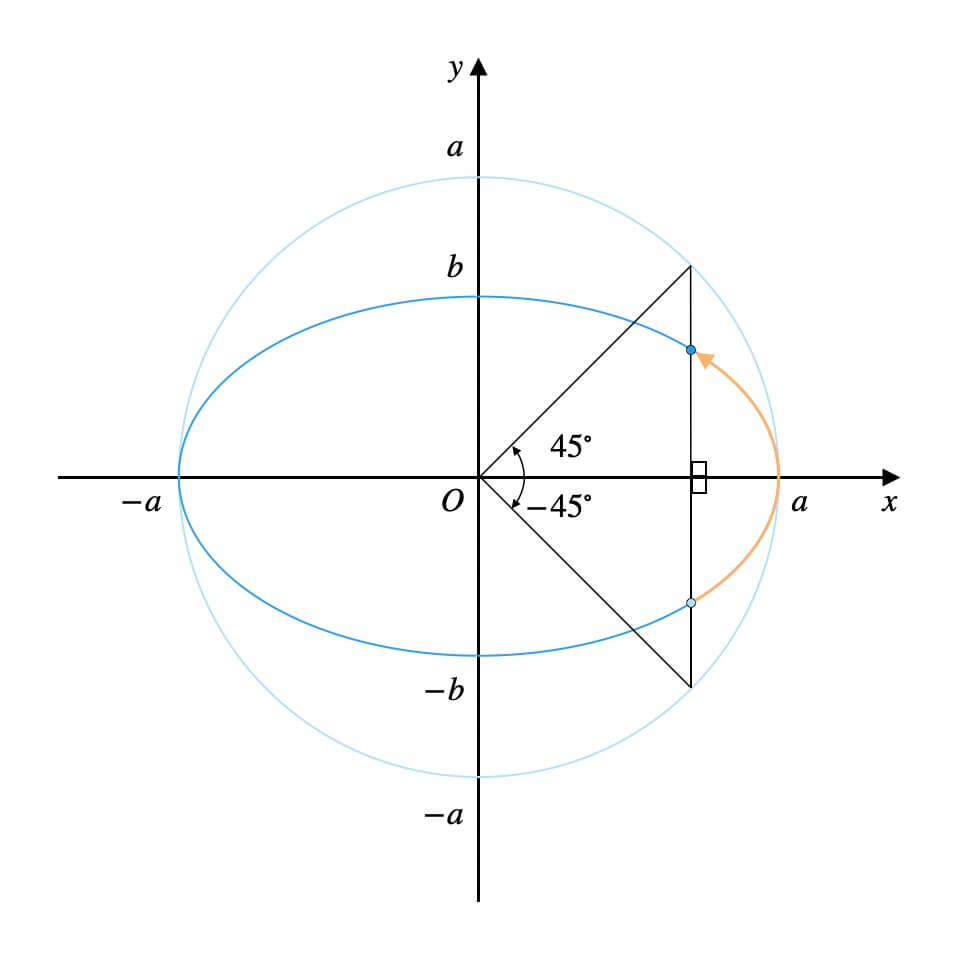
例えば、角度の範囲を\(0^\circ{}\)〜\(45^\circ{}\)とする場合。
多くの方が、次の弧を思い浮かべたのではないでしょうか。
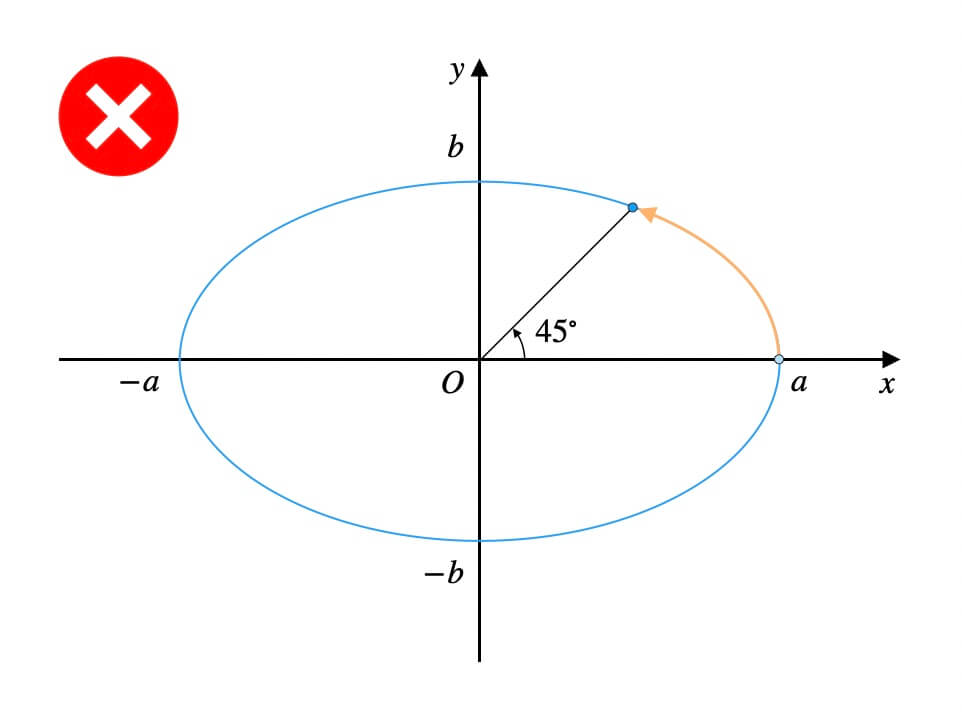
実はこれは誤りです。
よく見ると、\(45^\circ{}\)にしては扇形の面積比がおかしいですよね。
正しくは、次の図に示す範囲の弧です。
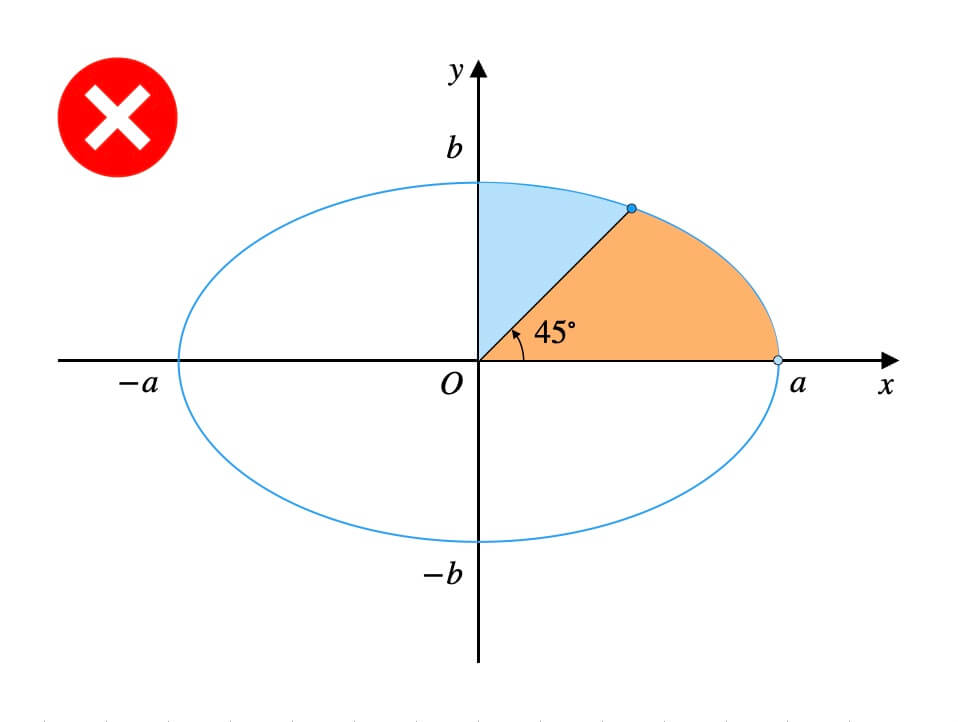
\(45^\circ{}\)とは、原点と円周上の点を結ぶ線分の偏角のことだったのです。
扇形の面積比もピッタリ同じです。
そもそも楕円周上の座標は、円を基準に媒介変数表示されるのでしたね。
角度を指定する理由
 すずか
すずか
 先生
先生
応用が効くように、プログラムは角度を指定する仕様にしました。
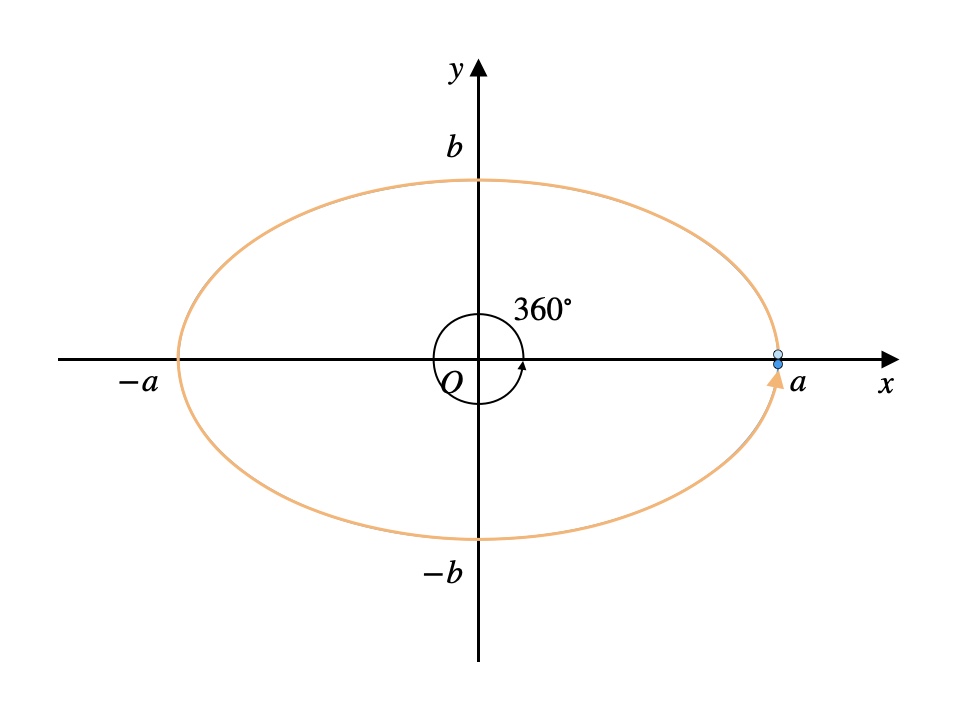
もちろん、楕円周上のすべての座標を取る場合にも対応しています。
角度の範囲を\(0^\circ{}\)〜\(360^\circ{}\)とすればいいですね。
キリの良い角度ではなく、中途半端な位置の弧の座標も取得できます。
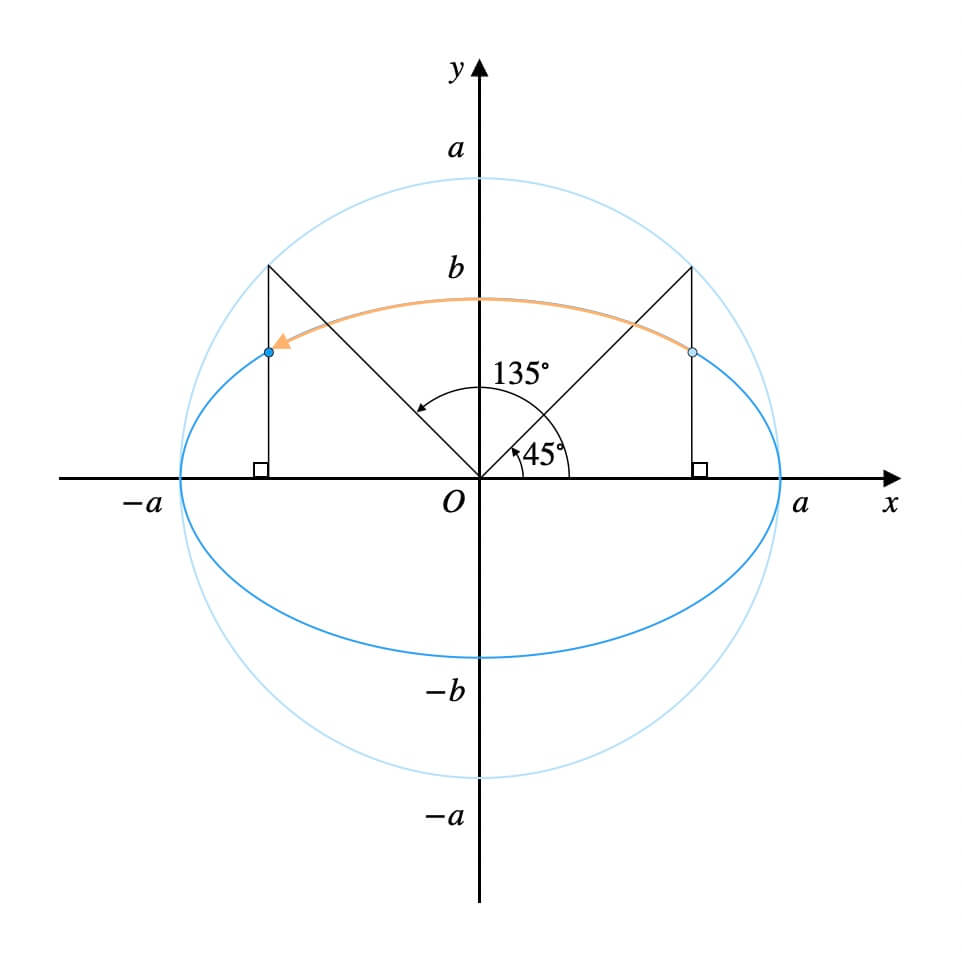
角度の範囲が\(45^\circ{}\)〜\(135^\circ{}\)の場合。
開始位置は負の角度からでもOKです。
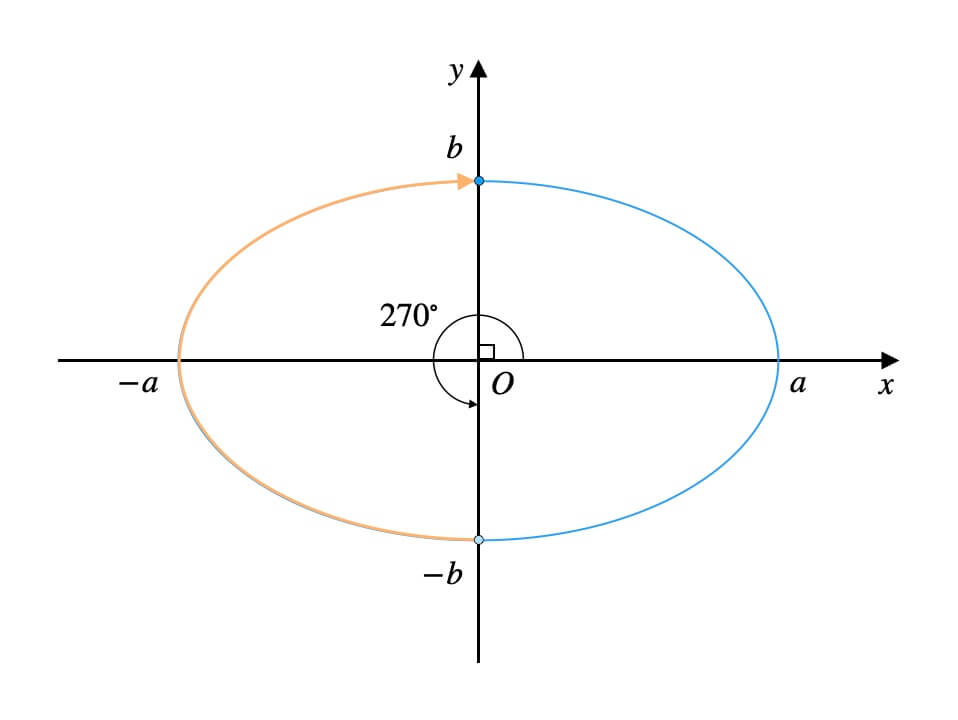
角度の範囲が\(-45^\circ{}\)〜\(45^\circ{}\)の場合。
逆方向から座標を取るのも朝飯前です。
角度の範囲が\(270^\circ{}\)〜\(90^\circ{}\)の場合。
テスト
座標が楕円周上に存在するかを確認
プログラムで得た座標が、本当に楕円周上に存在するかを確認します。
ある座標\((s, t)\)が楕円\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)上に存在するかを知るには、\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)の\(x\)に\(s\)、\(y\)に\(t\)を代入して式が成り立つかをチェックします。
- \(\frac{s^2}{a^2}+\frac{t^2}{b^2}=1\Leftrightarrow\)座標が楕円周上にある
- \(\frac{s^2}{a^2}+\frac{t^2}{b^2}\ne 1\Leftrightarrow\)座標が楕円周上にない
この事実を利用し、座標が楕円周上に存在するかを判定するプログラムを作ります。
import math import numpy as npdef is_point_on_ellipse(point, center, size): s, t = point p, q = center a, b = np.array(size) / 2 value = (s - p) ** 2 / a ** 2 + (t - q) ** 2 / b ** 2 return math.isclose(value, 1) def test_get_arc_coords(center, size, angle_range, is_radian=False, num_coords=None): # get_arc_coords関数を使用して楕円周上の座標を取得 coords = get_arc_coords(center, size, angle_range, is_radian, num_coords) # coordsの要素数 coord_len = len(coords) # 結果を格納するリスト results = [] # 取得した座標をループで処理 for i in range(0, coord_len, 2): # is_point_on_ellipse関数を使用して座標が楕円周上にあるか確認 result = is_point_on_ellipse( (coords[i], coords[i + 1]), (center_x, center_y), (width, height), ) # 結果をリストに格納 results.append(result) return all(results)
このプログラムは、get_arc_coords関数が返した座標群が楕円周上にあるか判定します。
def is_point_on_ellipse(point, center, size):
s, t = point
p, q = center
a, b = np.array(size) / 2
value = (s - p) ** 2 / a ** 2 + (t - q) ** 2 / b ** 2
return math.isclose(value, 1)is_point_on_ellipse関数は、ある座標が楕円周上に存在するかを判定します。
引数は、座標と楕円の情報です。
- point: 調べたい座標
- center: 楕円の中心座標
- size: 楕円の縦横のサイズ
戻り値は真偽値(ブール型)です。
- True: 座標(point)が楕円周上にある
- False: 座標(point)が楕円周上にない
それでは、次の3点を解説します。
引数のアンパックを行います。
s, t = point
p, q = center
a, b = np.array(size) / 2
- s: 判定したい\(x\)座標
- t: 判定したい\(y\)座標
- p: 楕円の中心の\(x\)座標
- q: 楕円の中心の\(y\)座標
- a: 楕円の半径(横)
- b: 楕円の半径(縦)
valueの右辺は、実は楕円の方程式です。
value = (s - p) ** 2 / a ** 2 + (t - q) ** 2 / b ** 2
value = \(\frac{(s-p)^2}{a^2}+\frac{(t-q)^2}{b^2}\)とするとわかりますね。
楕円の方程式に\(x=s, y=t\)を代入した形です。
valueに\(1\)が代入されれば、点\((s,\ t)\)が楕円\(\frac{(x-p)^2}{a^2}+\frac{(y-q)^2}{b^2}=1\)上にあります。
 すずか
すずか
 先生
先生
結論、楕円\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)を、\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させると、移動後の方程式は\(\frac{(x-p)^2}{a^2}+\frac{(y-q)^2}{b^2}=1\)になります。
次の数学的事実を利用しました。
曲線\(F(x,\ y)=0\)を、\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ平行移動させると、移動後の曲線の方程式は\(F(x-p,\ y-q)=0\)
例えば、取得した座標を指定の位置に平行移動の章で見たこの画像。
中心を\((p, q)\)に移動した楕円の方程式は、\(\frac{(x-p)^2}{a^2}+\frac{(y-q)^2}{b^2}=1\)だったのですね。
valueと\(1\)との比較に、math.isclose関数を使います。
return math.isclose(value, 1)
math.isclose関数は、ある\(2\)つの値を渡すと、それらが近似しているかを判定します。
\(0.99\cdots{}\)(\(9\)が\(9\)個)と\(1\)を比較しましょう。
a = 0.999999999 # 9が9個
print(math.isclose(a, 1))
# True
 すずか
すずか
デフォルトだと、\(2\)値が\(9\)桁同じだと近似していると判断されます。
 先生
先生
\(0.99\cdots{}\)の\(9\)を\(8\)個にしてみます。
a = 0.999999999 # 9が8個
print(math.isclose(a, 1))
# False\(9\)が\(9\)個だとTrueだったのに、\(8\)個にした途端にFalseになりました。
信頼できる精度ではないでしょうか。
 すずか
すずか
 先生
先生
実は、コンピュータは数値の誤差が生じます。
print(format(0.2, '.20f')) # 0.2を少数第20位まで表示 print(0.1 + 0.1 + 0.1 == 0.3) # 0.1+0.1+0.1と0.3が等しいかを判定 # 0.20000000000000001110 # False
脱線するので詳細は割愛しますが、コンピュータ内部で使われる\(2\)進数が原因です。
この問題に興味ある方は、Python公式ドキュメントをご覧ください。
座標計算では、必ず値の丸めが行われます。
真の値と誤差があるのは当然なので、近似値判定を導入しました。
def test_get_arc_coords(center, size, angle_range, is_radian=False, num_coords=None):
# get_arc_coords関数を使用して楕円周上の座標を取得
coords = get_arc_coords(center, size, angle_range, is_radian, num_coords)
# 取得した座標の数
coord_len = len(coords)
# 結果を格納するリスト
results = []
# 取得した座標をループで処理
for i in range(0, coord_len, 2):
# is_point_on_ellipse関数を使用して座標が楕円周上にあるか確認
result = is_point_on_ellipse(
(coords[i], coords[i + 1]),
(center_x, center_y),
(width, height),
)
# 結果をリストに格納
results.append(result)
return all(results)test_get_arc_coords関数は、get_arc_coords関数が生成した大量の座標が、全部楕円周上にあるかを判定します。
つまり、get_arc_coords関数の試験を担います。
引数はget_arc_coordsと同じです。
- center: 楕円の中心座標のタプル
- size: 楕円のサイズ(横\(×\)縦)のタプル
- angle_range: 弧の範囲の角度のタプル
- is_radian: 度数法か弧度法かを示すブール。デフォルトはFalse。
- num_coords: 座標の数の整数。デフォルトはNone。
戻り値は真偽値(ブール)です。
- True: テスト成功
- False: テスト失敗
以下では、関数内部の次の3つの処理を解説します。
\(1\): 問題用紙を見る
\(2\): 問題を解く
\(3\): 採点(\(0\)点 or \(100\)点)
と考えるとわかりやすいでしょう。
 先生
先生
まずは、テストする座標をget_arc_coords関数で生成します。
coords = get_arc_coords(center, size, angle_range, is_radian, num_coords)
coordsは、\(x\)座標と\(y\)座標が交互に入っています。
また、coord_lenはcoordsの要素数です。
print(coords)
# [x1, y1, x2, y2, ..., xn, yn]
coord_len = len(coords)
print(coord_len)
# 2nfor文では、座標が楕円周上にあるかを\(1\)つずつチェックしています。
results = []
for i in range(0, coord_len, 2):
result = is_point_on_ellipse(
(coords[i], coords[i + 1]),
(center_x, center_y),
(width, height),
)
results.append(result)
ループは\(0\)からcoord_len回までで、\(1\)つ飛ばしに回ります。
for i in range(0, coord_len, 2):これにより、points[i]で\(x\)座標を、points[i + 1]で\(y\)座標を必ず取得できます。
iとpoitns[i]・points[i + 1]の関係は、次のイメージをご覧ください。
# 楕円周上の座標(xとyの組)がn個分
coords = [x1, y1, x2, y2, ..., xn, yn]
# coordsの要素の個数(2n個)
coord_len = len(points)
for i in range(0, coord_len, 2):
print(i, coords[i], coords[i + 1])
# 0 x1 y1
# 2 x2 y2
# 4 x3 y3
# 中略
# 2n-2 xn yn
is_point_on_ellipse関数に調べたい座標と楕円の位置・サイズを渡します。
座標が楕円周上にあればTrueが、なければFalseがresultに入ります。
result = is_point_on_ellipse(
(coords[i], coords[i + 1]),
(center_x, center_y),
(width, height),
)
各resultをresultsに格納していきます。
results.append(result)
resultsの中身はこんなイメージです。
print(result)
# [True, True, True, True, ..., True]最後に、テストに失敗したケースが紛れていないかを確認します。
return all(results)
ちなみにall関数は、リスト内の要素が全てTrueのときに限り、Trueを返す関数です。
a = [True, True, True]
b = [True, False, True]
print(all(a))
print(all(b))
# True
# False
all(results)の戻り値はTrue or Falseですが、ここでは次の意味を持ちます。
- True: 全座標が楕円周上にある
- False: 楕円周上から外れている座標がある
試しに、次の条件で試験を行います。
- 中心座標: \((3, 2)\)
- サイズ(横\(×\)縦): \(12×8\)
- 弧の範囲の角度: \(45^\circ{}\)〜 \(135^\circ{}\)
# 楕円の中心座標
center_x = 3
center_y = 2
# 楕円の縦横のサイズ
width = 12
height = 8
# 弧の開始角度と終了角度
start_angle = 45
end_angle = 135
# get_arc_coords関数を使用して楕円周上の座標を取得
result = test_get_arc_coords(
(center_x, center_y),
(width, height),
(start_angle, end_angle),
)
結果です。
print(result)
# True取得した全座標が、楕円周上に存在することが保証されました!
一応、パラメータが適当でも成功しました。
# 楕円の中心座標
center_x = 3547389
center_y = 2432897
# 楕円の縦横のサイズ
width = 123421
height = 838219
# 弧の開始角度と終了角度
start_angle = 4324145
end_angle = 1354321
数値を変えて自由に試してみてくださいね。
座標を元に図形を描けるか?
次は、取得した座標で楕円や弧を描けるか確認します。
 すずか
すずか
 先生
先生
図形を視覚的に捉えるため、PythonのGUIライブラリであるTkitnerを使います。
import tkinter as tk
root = tk.Tk()
canvas = tk.Canvas(width=500, height=500)
canvas.pack()
root.mainloop()
コードを実行すると、画面が出現します。
この画面(に乗ったキャンバス)に図形を描いていきます。
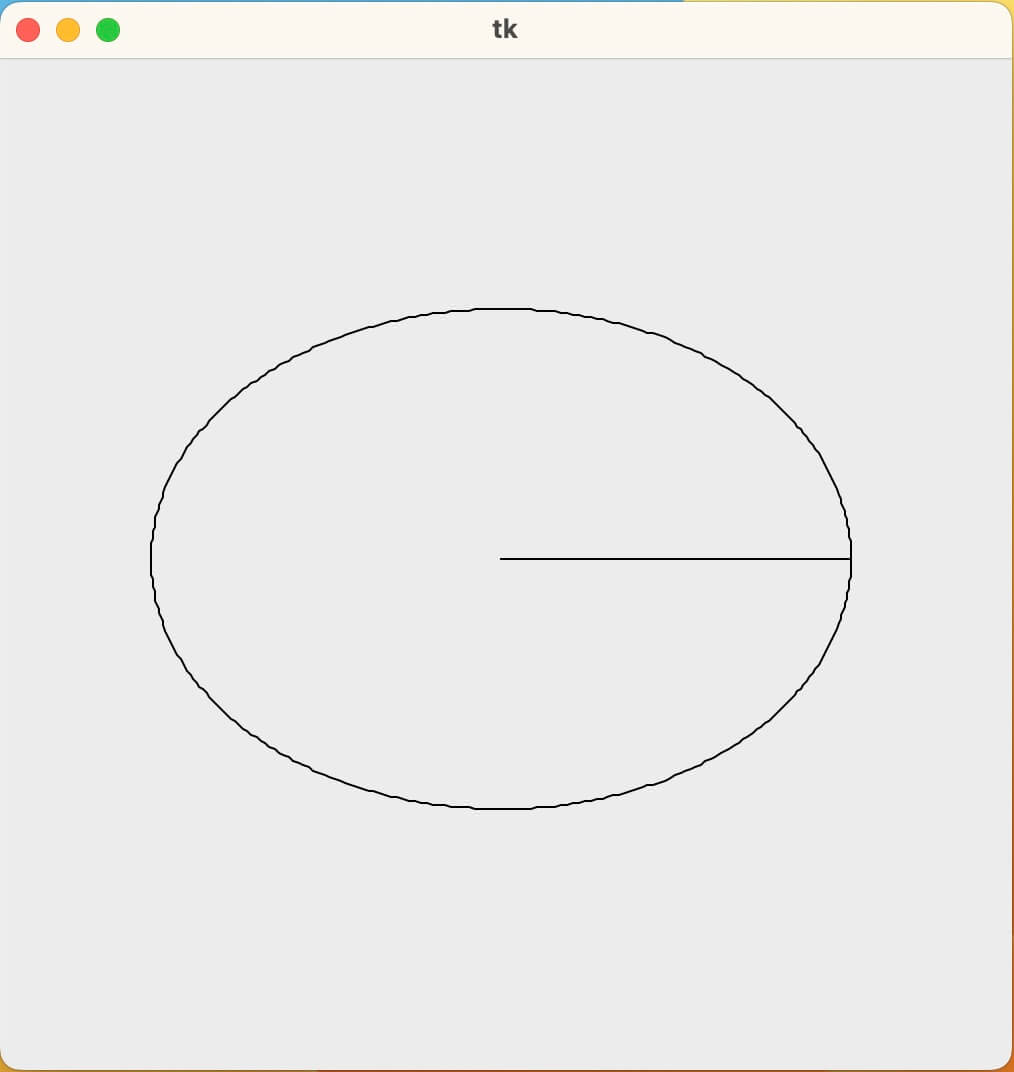
まずは、\(0^\circ{}\)〜\(90^\circ{}\)の範囲で描画します。
テスト対象は、次の楕円です。
- 中心座標: \((250, 250)\)
- サイズ(横\(×\)縦): \(350×250\)
- 角度の範囲: \(0^\circ{}\)〜 \(90^\circ{}\)
get_arc_coords関数を上で定義し、次のコードをroot.mainloop()の直前に埋め込みます。
center_x = 250
center_y = 250
width = 350
height = 250
start_angle = 0
end_angle = 90
coords = get_arc_coords(
(center_x, center_y),
(width, height),
(start_angle, end_angle),
)
canvas.create_polygon((center_x, center_y), coords, fill='', outline='black')
実行結果です。
 すずか
すずか
 先生
先生
右上ではなく右下に描画されたのは、Tkinterの座標系に起因します。 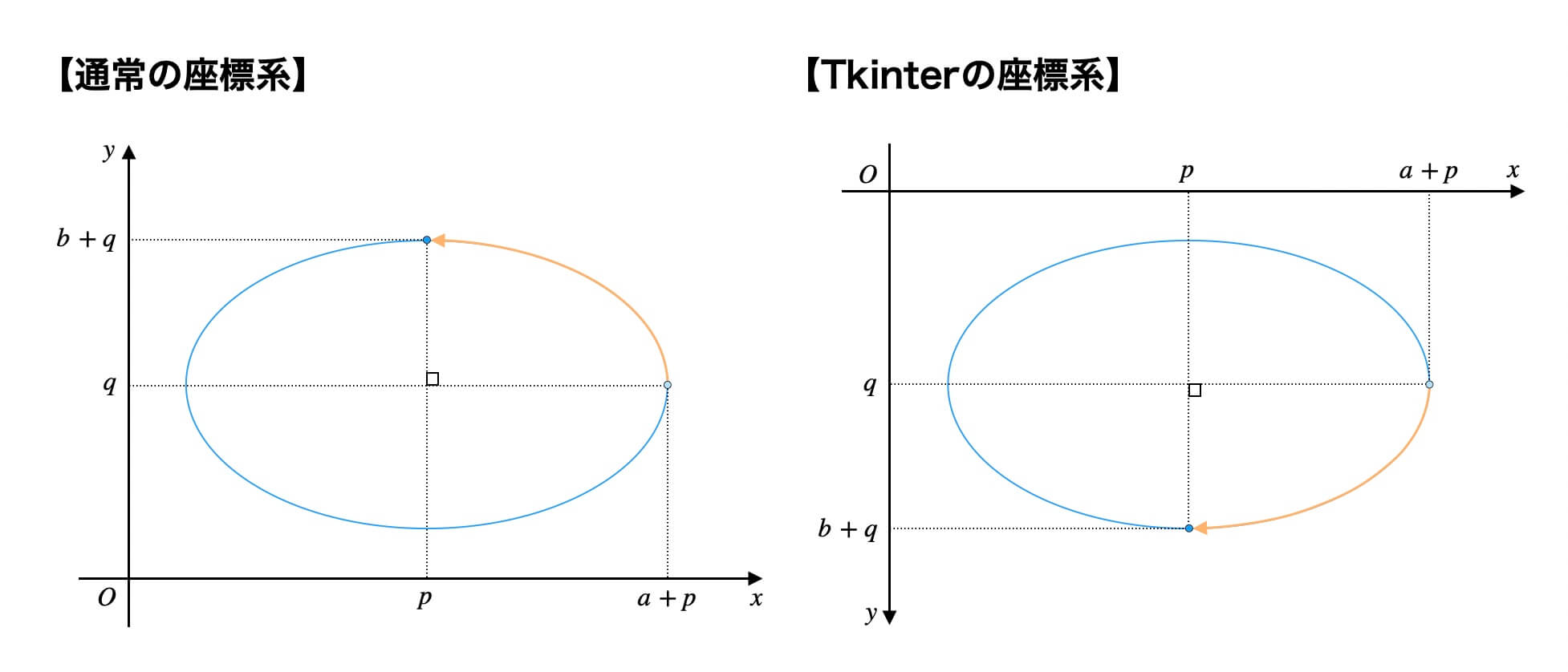
\(y\)軸の向きが上下逆のため、あたかも楕円の右下が描画されたように見えます。
したがって、テスト結果は正しいです。
次は、完全な楕円を描いてみましょう。
- 中心座標: \((250, 250)\)
- サイズ(横\(×\)縦): \(350×250\)
- 角度の範囲: \(0^\circ{}\)〜 \(360^\circ{}\)
get_arc_coords関数を上で定義し、次のコードをroot.mainloop()の直前に埋め込みます。
center_x = 250
center_y = 250
width = 350
height = 250
start_angle = 0
end_angle = 360
coords = get_arc_coords(
(center_x, center_y),
(width, height),
(start_angle, end_angle),
)
canvas.create_polygon((center_x, center_y), coords, fill='', outline='black')
実行結果です。
楕円ばかりで飽きてきましたね。
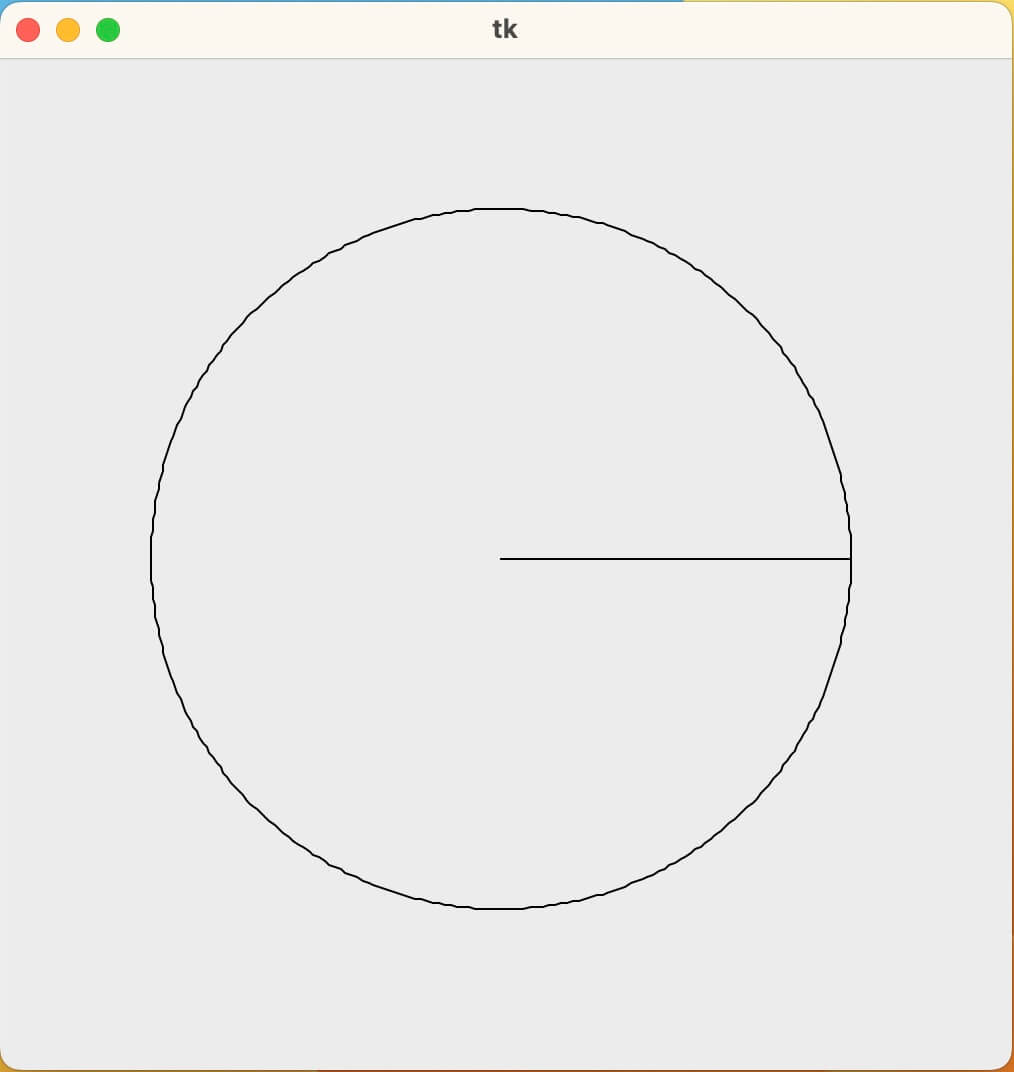
最後に真円を描いて締めましょう。
- 中心座標: \((250, 250)\)
- サイズ(横\(×\)縦): \(350×350\)
- 角度の範囲: \(0^\circ{}\)〜 \(360^\circ{}\)
get_arc_coords関数を上で定義し、次のコードをroot.mainloop()の直前に埋め込みます。
center_x = 250
center_y = 250
width = 350
height = 350
start_angle = 0
end_angle = 360
coords = get_arc_coords(
(center_x, center_y),
(width, height),
(start_angle, end_angle),
)
canvas.create_polygon((center_x, center_y), coords, fill='', outline='black')
実行結果です。
楕円周上の座標を求めるプログラムの活用
複雑な形状の図形作成
円や楕円の弧を利用して作る図形は、このプログラムを応用して描けます。
視力検査でお世話になるランドルト環です。
綺麗な円形矢印も描けます。
これらの図形を描画する方法は、また別の記事にまとめますね。
楕円の周長を計算
get_arc_coords関数で、楕円の周長や弧長の近似値を求められます。
半径\(r\)の円の周長は\(2\pi r\)ですね。
しかし、長径\(a\)・短径\(b\)の楕円の周長は\(4\int_{0}^{\frac{\pi}{2}} \sqrt{a^2\cos^2{t}+b^2\sin^2{t}}dt\)です。
不思議ですよね。
円周長はシンプルですが、楕円周長は簡単には表せないのです。
そこで、こんなプログラムを作ってみました。
import math
# 2点間の距離を求める関数
def get_distance(point1, point2):
x_diff = point1[0] - point2[0]
y_diff = point1[1] - point2[1]
return math.sqrt(x_diff ** 2 + y_diff ** 2)
# 弧の長さを求める関数
def get_arc_length(center, size, angle_range, is_radian=False, precision=None):
coords = get_arc_coords(center, size, angle_range, is_radian, precision)
length = 0
for i in range(0, len(coords) - 4, 2):
distance = get_distance(
(coords[i + 0], coords[i + 1]),
(coords[i + 2], coords[i + 3]),
)
length += distance
return length
楕円周上の座標が取れるならば、各座標間の距離を足し合わせて合計すればいいのです。
近似精度は引数precisionで調整できます。
実はもっと良い近似方法はありますが、詳細に関しては需要があれば記事にしますね。
まとめ
この記事では、楕円周上の座標を求めるプログラムを紹介しました。
楕円の方程式からも一応求められますが、媒介変数表示を利用するのがお勧めです。
媒介変数表示を使えば、たったの\(2\)ステップで求められるのでした。
グラフ作成はもちろん、図形との相性が抜群ですので、プログラムの活用場面は意外と身近に潜んでいますよ。
どんどん応用してみてくださいね。
最後までお付き合いいただき、ありがとうございました。