【Tkinter】アナログ時計の作り方！プログラミング練習に！

この記事の内容

アナログ時計のプログラム
アナログ時計をお洒落にするデザイン

こんにちは、Youta(@youta_blog)です。

今回は、Tkinterでアナログ時計を自作するお話です。

すずか

Tkinterにも慣れてきたし、何か手頃なもの作ろっかなー。

先生

では、アナログ時計を作ってはいかがでしょう？

アナログ時計とは、針が動く時計です。

実際にTkinterでアナログ時計のプログラムを作ってみました。

アナログ時計の自作は、特にプログラミング中級者の腕試しに最適です。

ウィジェットの操作や、時間の取得・三角関数の計算など、多様な分野の知識を試せます。

本記事では、解説・確認用コード・実行結果の3点をご用意しております。

また必要に応じてコードの解説をしていますので、初心者でも安心です。

記事の信頼性は、確認用コードと実行結果が保証します。

少しでも疑問に感じたら、是非ともコードをコピペしてPCで確かめてみてください。

それでは早速、Tkinterでアナログ時計を自作していきましょう。

設計

すずか

最初に大まかな流れ知っときたいんだけど？

結論、\(1\)秒ごとに各針の先端の座標を計算し、針を再描画すればOKです。

とはいえ、任意の時刻での各針の先端の座標を求めるのが、最も重要かつ難しい点です。

まず、計算が針の先端の座標を求めるだけで済む理由をお話しします。

時・分・秒の\(3\)本の針は\(2\)点を結ぶ線分で描きます。

\(2\)点のうちの\(1\)点は時計の中心ですよね。

したがって、もう一方の刻一刻と変化する針の先端の座標だけ求めれば良いのです。

詳しくは後ほど解説しますので、今は何となくで大丈夫です。

\(1\)秒ごとに各針の先端の座標を計算し、針を再描画するのが大まかな全体像です。

前置きはここまでにして、実際にプログラミングしていきましょう！

プリセット

まずはウィンドウとキャンバスを用意しましょう。

Tkinterをインポートして、ウィンドウとキャンバスを表示するコードを書きます。

import tkinter as tk

SIDE = 500  # ウィンドウの一辺
CENTER = SIDE / 2  # ウィンドウの中心

# ウィンドウの作成
root = tk.Tk()
root.title("Analog Clock")  # タイトル
root.geometry(f"{SIDE}x{SIDE}")  # 大きさ

# キャンバスの作成
canvas = tk.Canvas(root, width=SIDE, height=SIDE)
canvas.pack()

# ウィンドウの表示
root.mainloop()

実行すると、毎度お馴染みのウィンドウが出現します。

時計盤の描画

針や目盛りを乗せる時計盤を作りましょう。

TkinterのCanvasを使って時計の表示領域を作り、時計盤となる円を描画します。

CLOCK_FACE_RADIUS = SIDE / 2  # 時計盤の半径

# 時計盤を描画
clock_face = canvas.create_oval(
    0, 0,
    SIDE, SIDE,
    fill="white",
)

ウィンドウに円が現れました。

時計盤にフレームを付けたい場合は、円を複数重ねます。

おすすめは、外枠・内枠・時計盤の順に\(3\)つ円を描くことです。

INNER_FRAME_RADIUS = (SIDE * 0.85) / 2  # 内枠の半径
CLOCK_FACE_RADIUS = (SIDE * 0.8) / 2  # 時計盤の半径

# 外枠を描画
outer_frame = canvas.create_oval(
    0, 0,
    SIDE, SIDE,
)

# 内枠を描画
inner_frame = canvas.create_oval(
    CENTER - INNER_FRAME_RADIUS, CENTER - INNER_FRAME_RADIUS,
    CENTER + INNER_FRAME_RADIUS, CENTER + INNER_FRAME_RADIUS,
    fill="#bbbbbb",
    outline='#888888'
    width=SIDE * 0.01,
)

# 時計盤を描画
clock_face = canvas.create_oval(
    CENTER - CLOCK_FACE_RADIUS, CENTER - CLOCK_FACE_RADIUS,
    CENTER + CLOCK_FACE_RADIUS, CENTER + CLOCK_FACE_RADIUS,
    fill="white",
)

先生

色やサイズは好みに合わせてくださいね。

奥行きが生まれて立体感が出ました。

針のオブジェクトを作成

次に、時・分・秒の各針のオブジェクトを作成します。

座標は後ほど設定するので、今は適当で構いません。

# 時針の作成
hour_hand = canvas.create_line(
    0, 0, 0, 0,
    fill="blue",
    width=CLOCK_FACE_RADIUS * 0.04,
)

# 分針の作成
minute_hand = canvas.create_line(
    0, 0, 0, 0,
    fill="green",
    width=CLOCK_FACE_RADIUS * 0.02,
)

# 秒針の作成
second_hand = canvas.create_line(
    0, 0, 0, 0,
    fill="red",
    width=CLOCK_FACE_RADIUS * 0.01,
)

(一応、時針を青、分針を緑、秒針を赤にしておきます。)

上記のコードでは針は見えませんが、オブジェクト自体は\(3\)つ存在しています。

針の座標をうまい具合に設定した方は、見えているかも知れませんね。

現在時刻の取得

今が「何時何分何秒」なのかを求める関数を作ります。

Pythonで現在時刻を取得する方法はいくつかあります。

今回はtimeモジュールを使った一例をご紹介しましょう。

import time

def get_current_time():
    current_time = time.localtime()

    hour = current_time.tm_hour
    minute = current_time.tm_min
    second = current_time.tm_sec

    return hour, minute, second

現在の時間・分・秒を教えてくれるget_current_time関数を作りました。

戻り値

変数名	データ型	説明
`hour`	整数	現在の時間
`minute`	整数	現在の分
`second`	整数	現在の秒

get_current_time関数の戻り値

戻り値を受け取る変数の数に応じて、挙動が変わります。

# 1つの変数を使用する場合
time_tuple = get_current_time()
print(time_tuple)
# (17, 14, 24)

# 3つの変数を使用する場合
hour, minute, second = get_current_time()
print(hour, minute, second)
# 17 14 24

針先の座標の計算

現在時刻から、\(3\)本の針の先端がそれぞれどの位置にあるかを計算します。

ここから少し難しくなりますが、一緒に頑張りましょう。

先に結論を述べると、次の式で求まります。

針の先端の座標

\(x\)座標:　\(針の長さ × \cos{(針の角度)} + 時計の中心のx座標\)
\(y\)座標:　\(針の長さ × \sin{(針の角度)} + 時計の中心のy座標\)

すずか

わけわからん。

先生

大丈夫です。

実は、次の\(4\)つを一気にやっているだけです。

針の先端の座標の求め方

針の角度を求める。
①の角度に対応する単位円周上の座標を求める。
座標に針の長さを掛け合わせる。
座標を平行移動する。

針の角度を計算

後ほど登場する\(\sin{\theta}\)や\(\cos{\theta}\)の引数である\(\theta\)に入れる角度を求めます。

現在時刻をもとに、何かしらの意味を持つ角度を返す関数を作るイメージです。

先に結論を述べると、次の式で求まります。

針の角度

時針:　\(時 × 30°+ 分 × 0.5° – 90°\)
分針:　\(分 × 6° + 秒 × 0.1° – 90°\)
秒針:　\(秒 × 6° – 90°\)

これらが\(\sin{\theta}\)や\(\cos{\theta}\)の\(\theta\)に相当します。

この式でやっていることは次の\(2\)つです。

針の角度の求め方

針が\(0\)時から時計回りに何度回転しているかを求める。
①の角度から\(90°\)を引く。

0時からの針の進み

「時・分・秒」をもとに、各針が\(0\)時から時計回りに何度回転しているかを求めます。

先に結論を述べると、次の式で求まります。

0時からの針の進み

時針:　\(時 × 30°+ 分 × 0.5°\)
分針:　\(分 × 6° + 秒 × 0.1°\)
秒針:　\(秒 × 6°\)

寝起きで式を見ると混乱しそうですが、よく考えるとすぐに理解できるはずです。

秒針は\(1\)分(\(60\)秒)で\(1\)周、つまり\(360°\)回転します。

ということは、秒針は\(1\)秒で\(6°\)回転します。

ですから、\(0\)時からの角度は、秒\(×6°\)となるのです。

同様に、分針は\(1\)時間(\(60\)分)で\(1\)周、つまり\(360°\)回転します。

ということは、分針は\(1\)分(\(60\)秒)で\(6°\)回転します。

さらに、分針は\(1\)秒で\(0.1°\)回転しますよね。

ですから、\(0\)時からの角度は、\(分 × 6° + 秒 × 0.1°\)となるのです。

最後に、時針は\(12\)時間(\(720\)分)で\(1\)周、つまり\(360°\)回転します。

ということは、時針は\(1\)時間(\(60\)分)で\(30°\)回転します。

さらに、時針は\(1\)分で\(0.5°\)回転しますよね。

ですから、\(0\)時からの角度は、\(時 × 30°+ 分 × 0.5°\)となるのです。

まとめます。

0時からの針の進み

時針:　\(時 × 30°+ 分 × 0.5°\)
分針:　\(分 × 6° + 秒 × 0.1°\)
秒針:　\(秒 × 6°\)

-90°の謎

さて、この章では先程求めた角度から\(90°\)を引く理由を解き明かします。

結論、Tkinterの座標系における単位円の始線を、\(90°\)後方に設定するためです。

簡単に言えば、三角関数の定義とTkinterの座標系との辻褄合わせです。

すずか

わかんな。

先生

丁寧に説明するので安心してください！

\(-90°\)がないと、何がまずいのかを考えると良いですよ。

まずは、数学での一般的な座標の取り方とTkinterの座標の取り方の違いをお見せします。

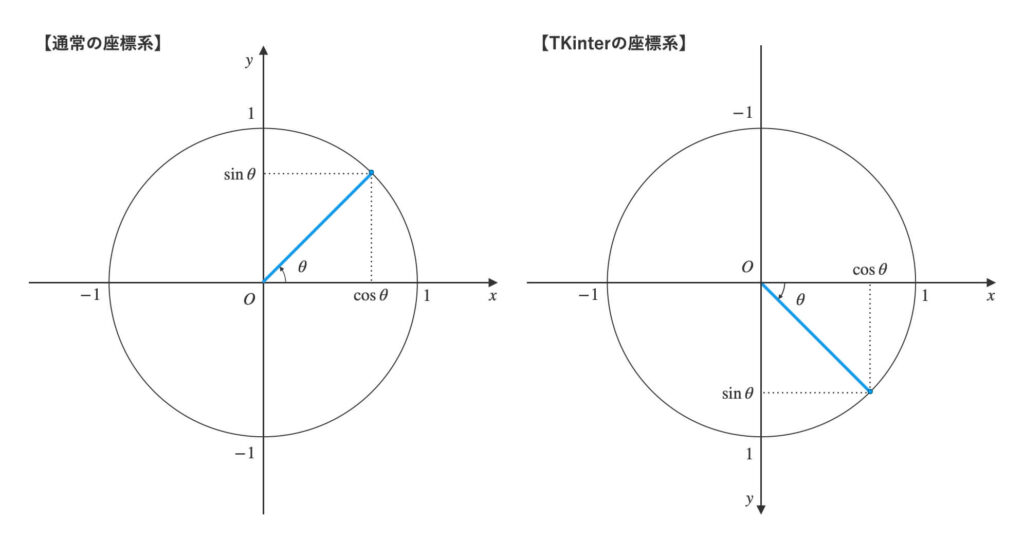
\(y\)軸の向き・動径の動く向きが真逆です。

例えば今が\(6\)時だとします。

時針は\(0\)時から時計回りに\(180°\)回転していますね。

この\(180°\)から\(90°\)を引かず、\(\theta=180°\)として\(\sin{\theta}\)と\(\cos{\theta}\)を計算するとどうなるでしょう。

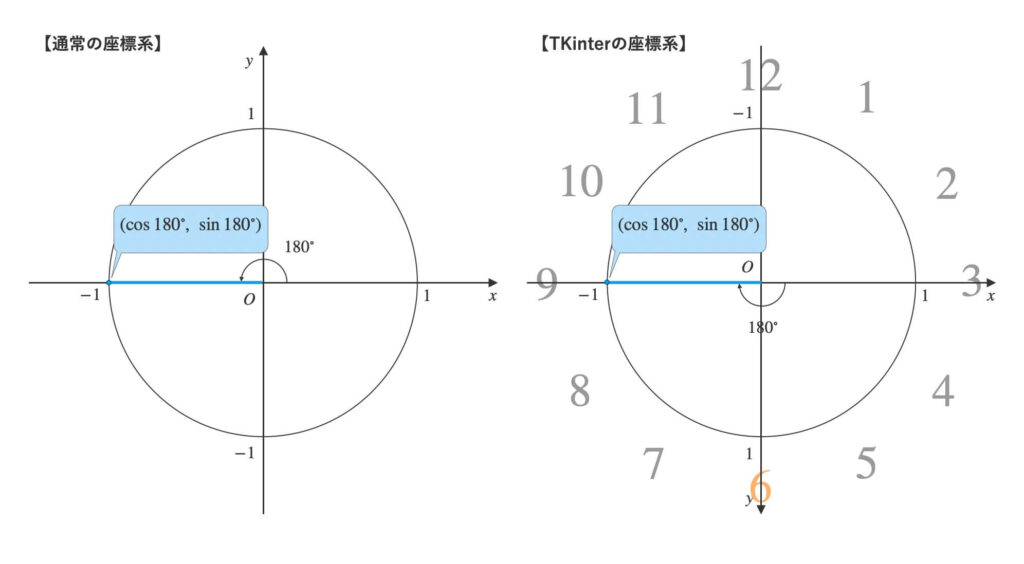
あれ、Tkinterの座標系での単位円では、\(9\)時の座標になってしまいましたね。

すずか

あーあ。あと\(90°\)後ろだったら良いのにね。

先生

良い着眼点です！

そのままだと\(90°\)分超過してしまうので、最初から\(90°\)を引くのです。

今度は、事前に\(180°\)から\(90°\)を引き、\(\theta=90°\)として\(\sin{\theta}\)と\(\cos{\theta}\)を計算してみましょう。

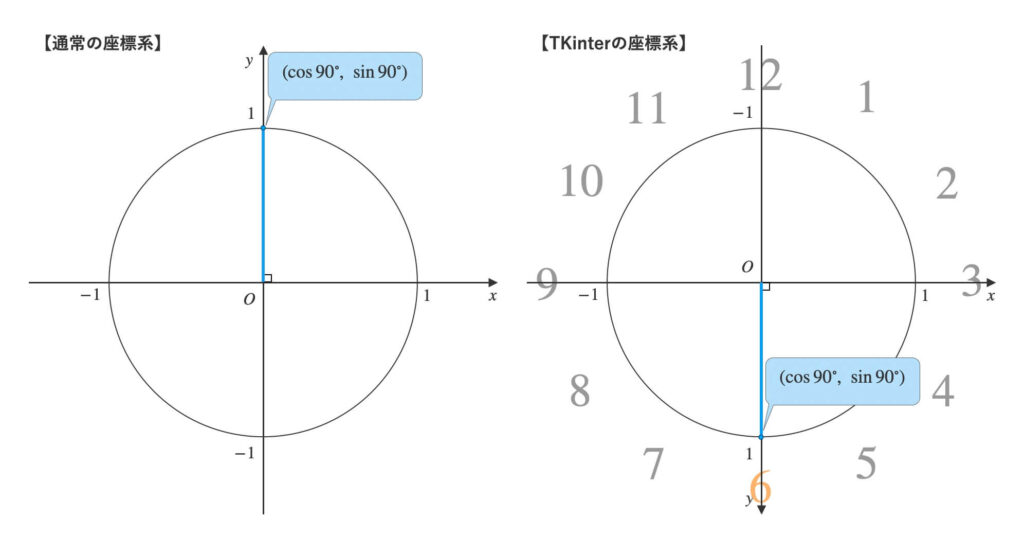
Tkinterの座標系での単位円では、\(6\)時の座標が取れていますね！

Tkinterの座標系における単位円は、私たちから見て始線が\(3\)時の向きにあります。

角度から\(90°\)を引くことで、始線を\(0\)時の向きに合わせる、とも捉えられますね。

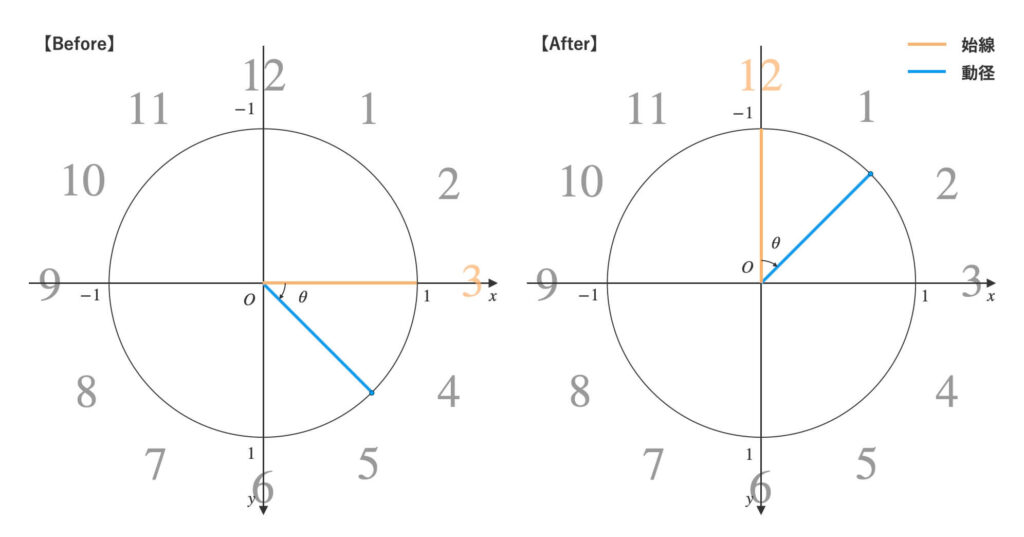
難しかった方は、「とりあえず\(-90°\)すれば良いんだな〜」くらいの認識で大丈夫です。

まとめます。

針の角度

時針:　\(時 × 30°+ 分 × 0.5° – 90°\)
分針:　\(分 × 6° + 秒 × 0.1° – 90°\)
秒針:　\(秒 × 6° – 90°\)

以上を踏まえると、下記のコードが書けます。

import math

# 現在時刻の取得
hour, minute, second = get_current_time()

# 針の角度の計算
hour_angle = math.radians((hour * 30) + (minute * 0.5)　- 90)
minute_angle = math.radians((minute * 6) + (second * 0.1) - 90)
second_angle = math.radians(second * 6 - 90)

radians関数は、角度を度数法から弧度法に変えています。

角度に対応する単位円周上の座標を計算

針の角度に対応する単位円周上の座標を求めます。

三角関数の定義により、次の式で座標が出ます。

針の角度に対応する単位円周上の座標

\(x\)座標:　\(\cos{(針の角度)}\)
\(y\)座標:　\(\sin{(針の角度)}\)

例えば、今が\(10\)時ぴったりだとしましょう。

時針の角度は、\(時 × 30°+ 分 × 0.5° – 90°\)の公式を使うと、\(10 × 30°+ 0 × 0.5° – 90° = 210°\)です。

よって、\(\theta=210°\)として\(\sin{\theta}\)と\(\cos{\theta}\)を計算します。

この部分の座標が取れたことになります。

先生

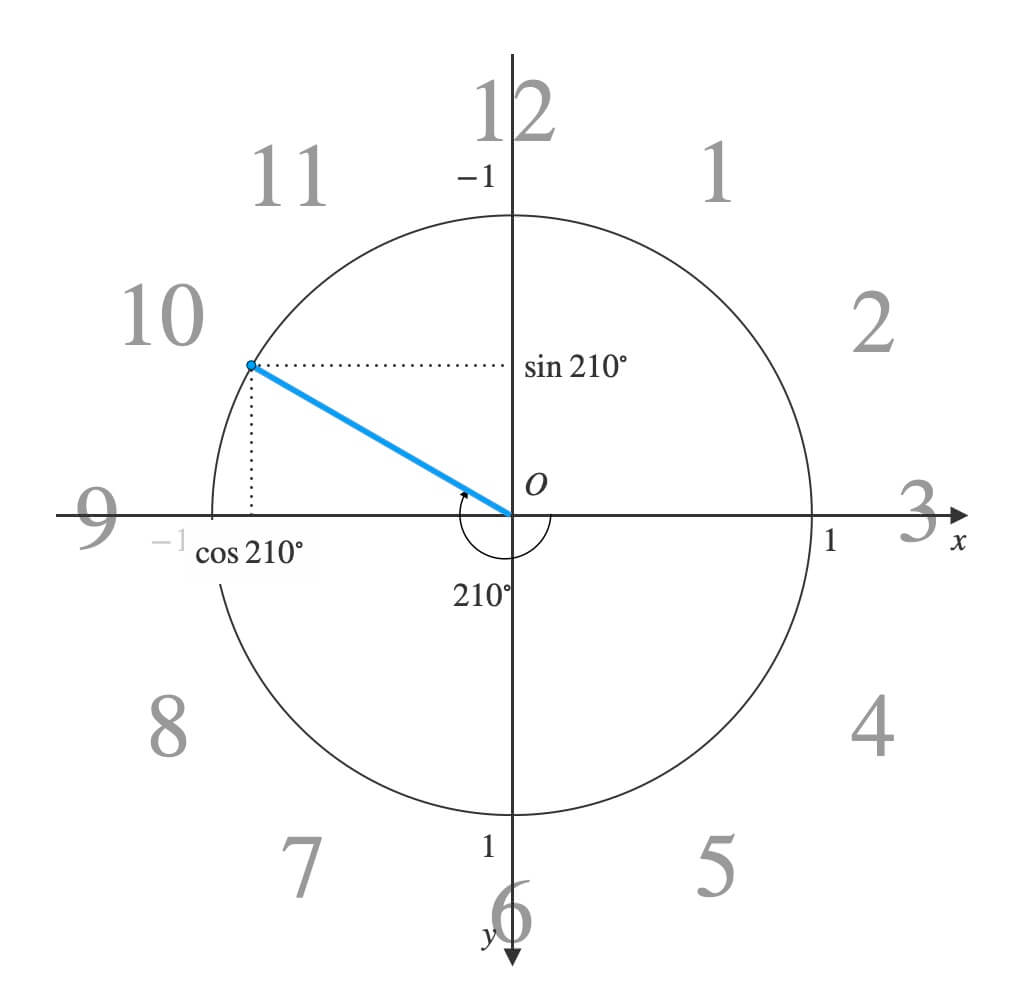
ちなみに\(\cos{210°}\)は\(-\frac{\sqrt{3}}{2}\)で、\(\sin{210°}\)は\(-\frac{1}{2}\)です。

針の長さに合わせて単位円を拡大

先ほど求めた\(x\)座標と\(y\)座標に針の長さを掛けます。

計算式にするとこんな感じです。

針の長さに合わせて単位円を拡大

\(x\)座標:　\(針の長さ × \cos{(針の角度)}\)
\(y\)座標:　\(針の長さ × \sin{(針の角度)}\)

例えば、時針の長さを\(6\)とすると、拡大後は\((6\cos{210°},\ 6\sin{210°})\)に移動します。

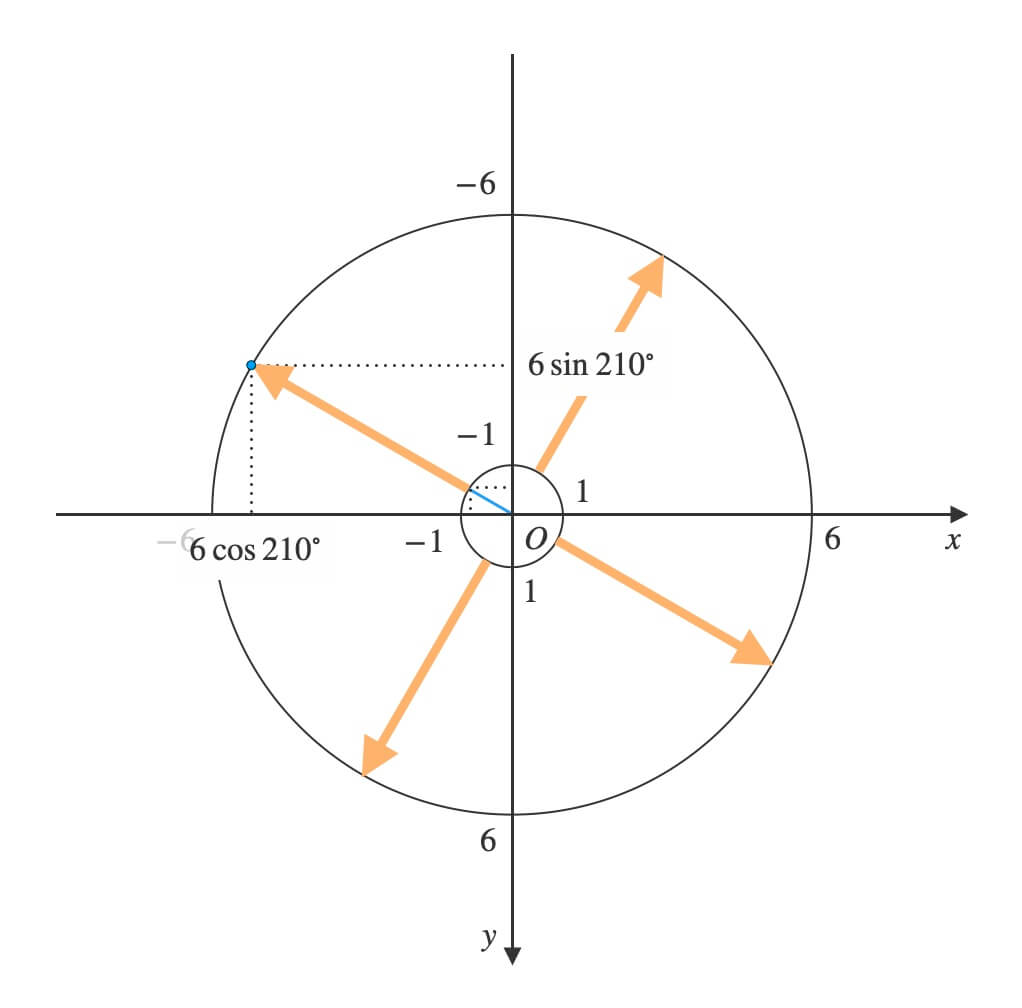
方向を保ったまま、欲しい長さまで座標を引き伸ばすイメージです。

座標を平行移動

いよいよ最終段階、座標をウィンドウ領域に平行移動させます。

計算方法は、先ほどの\(x\)座標と\(y\)座標に画面中央の座標を追加するだけです。

先ほどの座標に、時計の中心の座標を追加します。

針の先端の座標

\(x\)座標:　\(針の長さ × \cos{(針の角度)} + 時計の中心のx座標\)
\(y\)座標:　\(針の長さ × \sin{(針の角度)} + 時計の中心のy座標\)

先ほど見た複雑な計算式が再登場しました。

針の長さを半径とする円を、時計盤の真ん中に持ってくるイメージです。

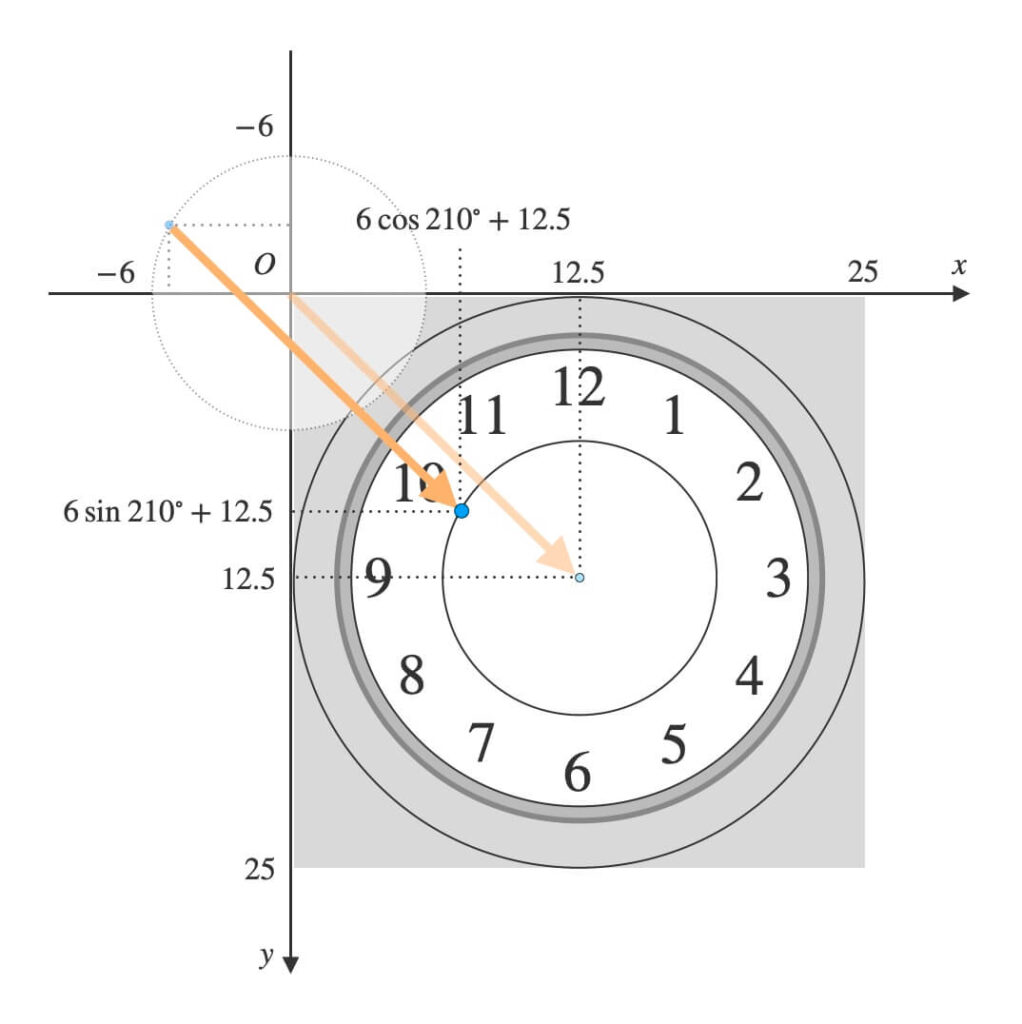
その後、時針の先端の座標と時計盤の中心座標とを結ぶ線分を描けば、時針の完成です。

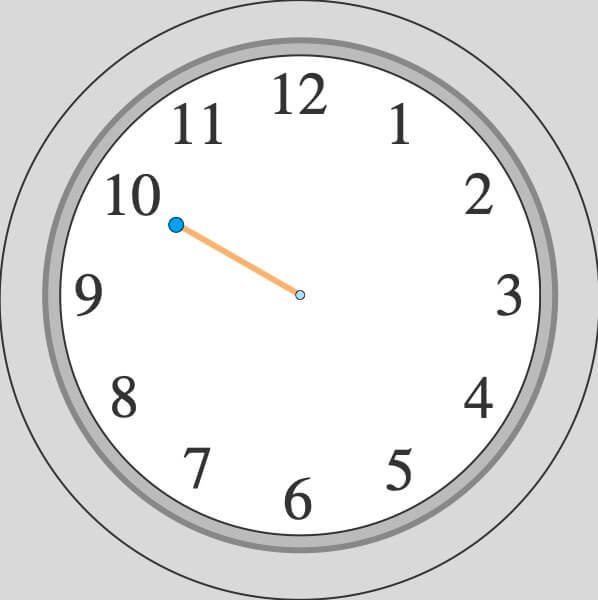
以上をまとめます。

針の先端の新しい位置を求め、針を再描画します。

# 針の長さ
hour_hand_length = CLOCK_FACE_RADIUS * 0.6
minute_hand_length = CLOCK_FACE_RADIUS * 0.9
second_hand_length = CLOCK_FACE_RADIUS * 0.9

# 時針の移動
canvas.coords(
    hour_hand,
    CENTER,
    CENTER,
    hour_hand_length * math.cos(hour_angle) + CENTER,
    hour_hand_length * math.sin(hour_angle) + CENTER,
)

# 分針の移動
canvas.coords(
    minute_hand,
    CENTER,
    CENTER,
    minute_hand_length * math.cos(minute_angle) + CENTER,
    minute_hand_length * math.sin(minute_angle) + CENTER,
)

# 秒針の移動
canvas.coords(
    second_hand,
    CENTER,
    CENTER,
    second_hand_length * math.cos(second_angle) + CENTER,
    second_hand_length * math.sin(second_angle) + CENTER,
)

これにより、どんな時刻でも計算された角度に基づいて針が正確に移動します。

時計の更新

最後に、時間が経過するごとに時計を更新する関数を作成しましょう。

これまでの章の内容をまとめました。

def tick():
    # 現在時刻の取得
    hour, minute, second = get_current_time()

    # 針の角度の計算
    hour_angle = math.radians((hour * 30) + (minute * 0.5) - 90)
    minute_angle = math.radians((minute * 6) + (second * 0.1) - 90)
    second_angle = math.radians(second * 6 - 90)

    # 針の長さ
    hour_hand_length = CLOCK_FACE_RADIUS * 0.6
    minute_hand_length = CLOCK_FACE_RADIUS * 0.9
    second_hand_length = CLOCK_FACE_RADIUS * 0.9

    # 時針の移動
    canvas.coords(
        hour_hand,
        CENTER,
        CENTER,
        hour_hand_length * math.cos(hour_angle) + CENTER,
        hour_hand_length * math.sin(hour_angle) + CENTER,
    )

    # 分針の移動
    canvas.coords(
        minute_hand,
        CENTER,
        CENTER,
        minute_hand_length * math.cos(minute_angle) + CENTER,
        minute_hand_length * math.sin(minute_angle) + CENTER,
    )

    # 秒針の移動
    canvas.coords(
        second_hand,
        CENTER,
        CENTER,
        second_hand_length * math.cos(second_angle) + CENTER,
        second_hand_length * math.sin(second_angle) + CENTER,
    )

    # 1秒ごとに更新
    root.after(1000, tick)


# 時計の更新を開始
tick()

指定時間後に関数を呼ぶafterメソッドは、秒数をミリ秒で指定します。

    # 1秒ごとに更新
    root.after(1000, tick)  # 1000ミリ秒 = 1秒

実行してみます。

現在時刻に合わせて針が動く、アナログ時計が完成しました。

すずか

なんか物足りないなー。

先生

そうですよね。

一応、次章以降でカスタマイズできますよ。

現時点で、一応最低限の機能を持つアナログ時計を作りました。

「もうお腹いっぱい！」と感じる方は、記事から離脱していただいて構いません。

「いや、もっとスタイリッシュにしたい！」と思う方は、次章にお進みください。

目盛りの描画

時計に目盛りを刻んでいきます。

刻み方を\(2\)通り用意しましたので、お好みに合わせてお選びください。

目盛りの細かさ

\(1\)分刻み:　計\(60\)個の目盛りを刻む
\(5\)分刻み:　計\(12\)個の目盛りを刻む

1分刻み

時計盤に\(1\)分刻みで目盛りを入れます。

下記のdraw_tick_marks関数を呼んでください。

def draw_tick_marks():
    for i in range(60):
        # 目盛りの角度を計算
        angle = math.radians(6 * i - 90)

        sin_angle = math.sin(angle)
        cos_angle = math.cos(angle)

        # 目盛りの始点座標
        if i % 5 == 0:
            distance_from_center = CLOCK_FACE_RADIUS * 0.825
        else:
            distance_from_center = CLOCK_FACE_RADIUS * 0.925

        start_x = distance_from_center * cos_angle + CENTER
        start_y = distance_from_center * sin_angle + CENTER

        # 目盛りの終点座標
        distance_from_center = CLOCK_FACE_RADIUS * 0.975

        end_x = distance_from_center * cos_angle + CENTER
        end_y = distance_from_center * sin_angle + CENTER

        # 目盛りの太さを設定
        if i % 15 == 0:
            line_width = CLOCK_FACE_RADIUS * 0.04
        elif i % 5 == 0: 
            line_width = CLOCK_FACE_RADIUS * 0.02
        else:
            line_width = CLOCK_FACE_RADIUS * 0.01

        # キャンバス上に目盛りを描画
        canvas.create_line(
            start_x, start_y,
            end_x, end_y,
            width=line_width,
        )

draw_tick_marks関数は、針の描画前に呼んで下さい。
動作上は問題ありませんが、針が目盛りの下に埋もれてしまい、見栄え上よくありません。

よく見るアナログ時計ですね。

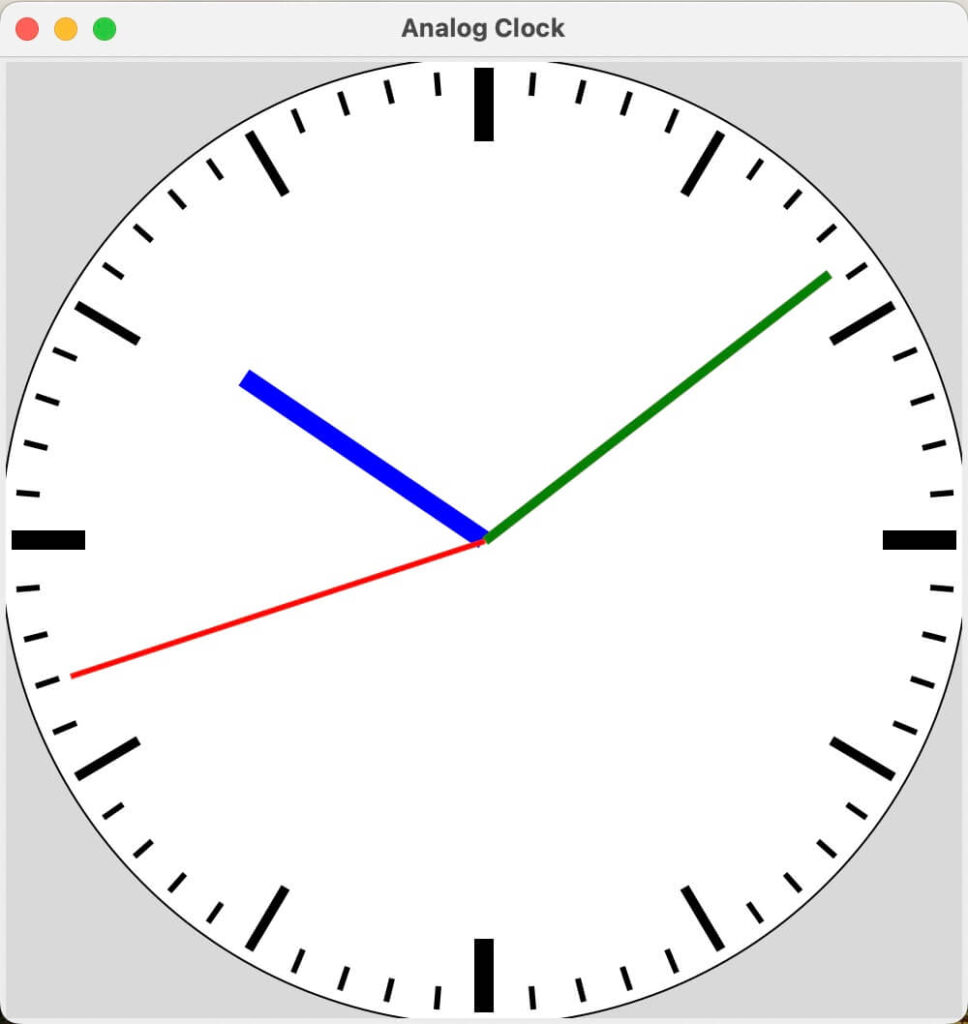
5分刻み

時計盤の目盛りを\(5\)分刻みにしてみましょう。

先ほどのfor文の冒頭で、分が\(5\)の倍数でなければループを飛ばすようにすればOKです。

    for i in range(60):
        if i % 5 != 0:
            continue

        # 目盛りの角度を計算
        angle = math.radians(6 * i - 90)

        ...

これはこれでシンプルで良いですね。

数字の描画

やはり時計といえば、数字ですよね。

この章では、時計盤に数字を付ける関数をご紹介します。

draw_numbers関数で、時計盤に数字を描画できます。

def draw_numbers():
    for i in range(12):
        # 数字の角度を計算
        number_angle = math.radians(30 * i - 60)
        
        # 数字の座標を計算
        distance_from_center = CLOCK_FACE_RADIUS * 0.7

        x = distance_from_center * math.cos(number_angle) + CENTER
        y = distance_from_center * math.sin(number_angle) + CENTER
        
        # キャンバス上に数字を描画
        canvas.create_text(
            x, y,
            text=str(i + 1),
            font=("Helvetica", int(CLOCK_FACE_RADIUS * 0.25)),
        )

draw_numbers関数は、針の描画前に呼んで下さい。
動作上は問題ありませんが、針が数字の下に埋もれてしまい、見栄え上よくありません。

せっかくなので、draw_tick_marks関数と一緒に呼んでみました。

数字のありなしは、好みが分かれるかも知れませんね。

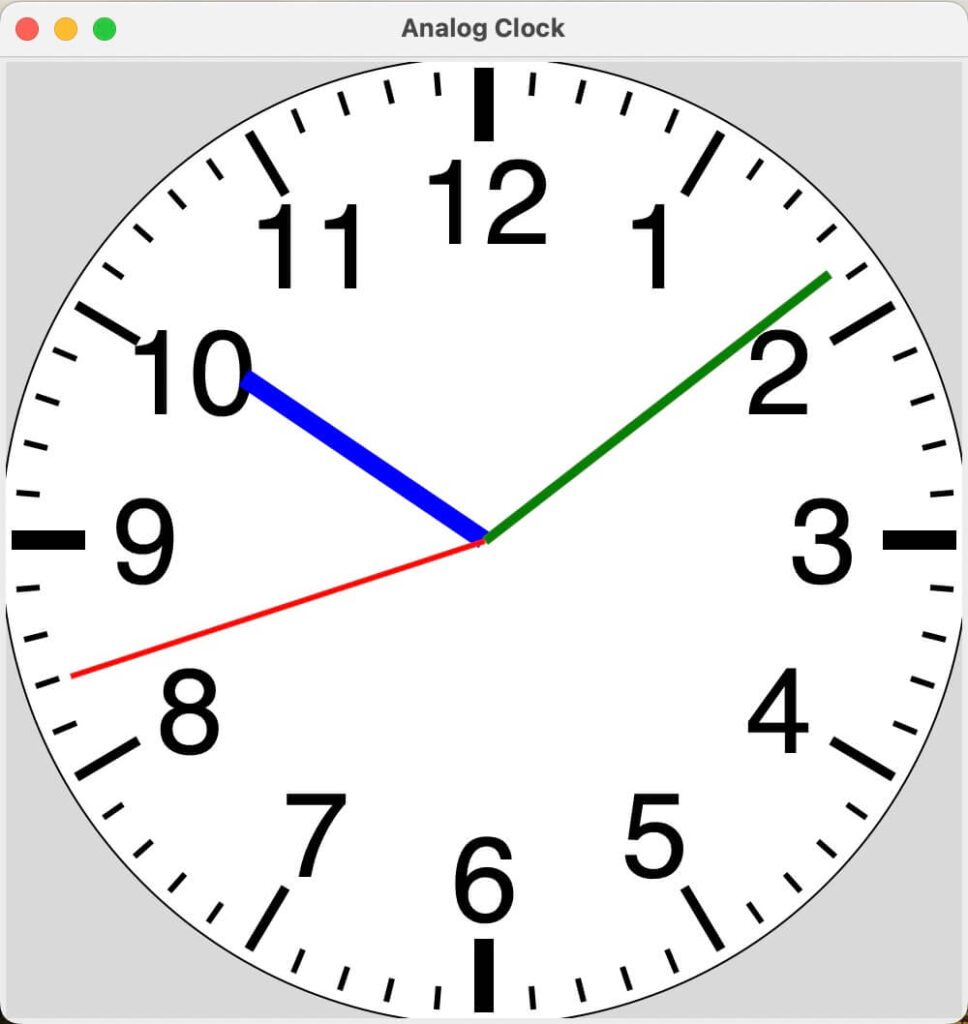
その他のデザイン

先生

ようこそ、自己満足の世界へ。

やはりデザインはとても大切ですよね。

みなさんも腕時計を買うときは、価格と同じくらい見た目も重視するはずです。

ということで、この章ではデザインに特化してお話しします。

ピン

\(3\)本の針を時計版に固定するピンを描画します。

コードは秒針の描画の直後に入れると良いでしょう。

# 留め具の描画
pin = canvas.create_oval(
    CENTER - CLOCK_FACE_RADIUS * 0.02,
    CENTER - CLOCK_FACE_RADIUS * 0.02,
    CENTER + CLOCK_FACE_RADIUS * 0.02,
    CENTER + CLOCK_FACE_RADIUS * 0.02,
    fill="white",
)

ど真ん中にピンが刺さりました。

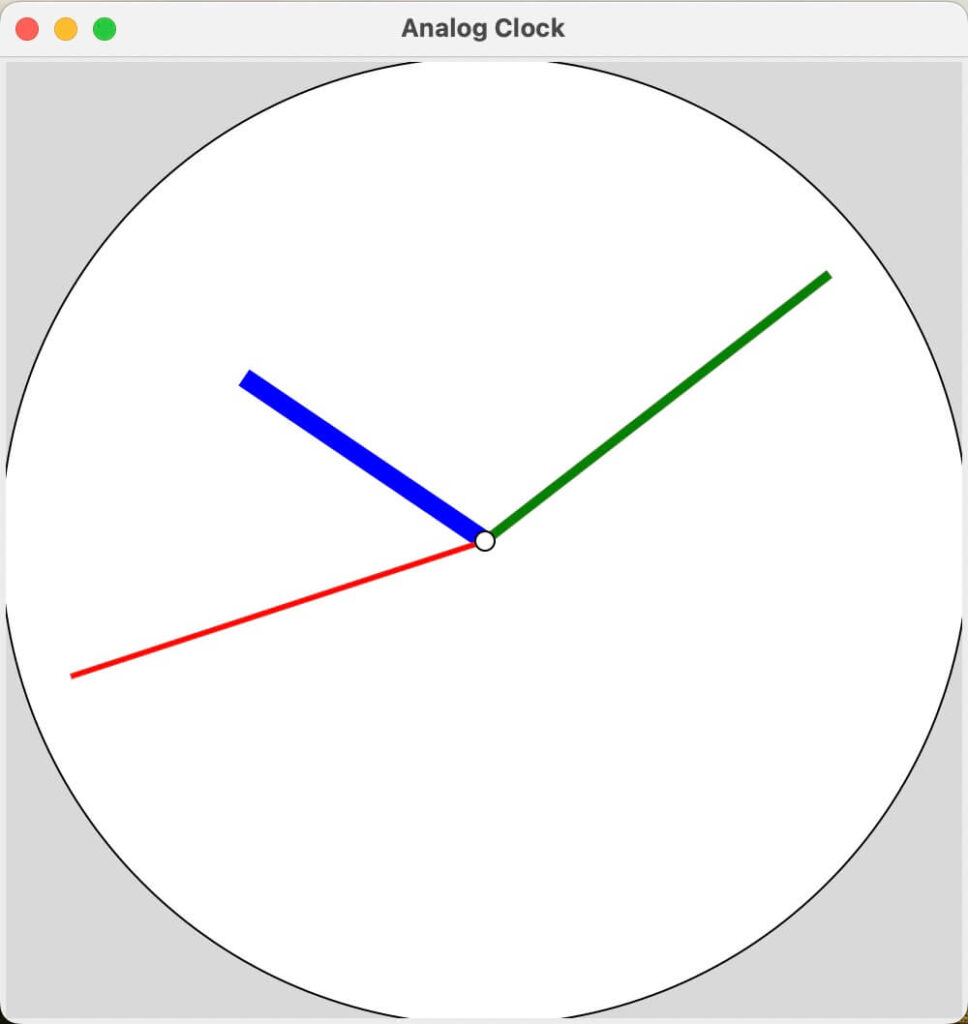
これで間違っても針は飛んでいきません。

針の尻尾

針を中心よりも後方に少しだけ伸ばします。

その座標は、次のように計算できます。

針の末端の座標

\(x\)座標:　\(針後方の長さ × \cos{(針の角度 – 180°)} + 時計の中心のx座標\)
\(y\)座標:　\(針後方の長さ × \sin{(針の角度 – 180°)} + 時計の中心のy座標\)

先生

主に\(-180\)の部分が、針の先端を求める計算式と異なります。

理屈は先ほどと全く同じです。

後ろに針を伸ばしたいので、針の角度と真逆の方向、つまり\(180°\)を引いているのです。

先生

\(180°\)を引く代わりに、足しても良いですよ。

tick関数内で各針の座標を更新している箇所を、下記のように書き換えてください。

    # 針の角度と逆向きの角度
    reversed_hour_angle = hour_angle - math.pi
    reversed_minute_angle = minute_angle - math.pi
    reversed_second_angle = second_angle - math.pi

    # 針の後ろの長さ
    hour_hand_tail_length = CLOCK_FACE_RADIUS * 0.2
    minute_hand_tail_length = CLOCK_FACE_RADIUS * 0.2
    second_hand_tail_length = CLOCK_FACE_RADIUS * 0.2

    # 時針の移動
    canvas.coords(
        hour_hand,
        hour_hand_length * math.cos(hour_angle) + CENTER,
        hour_hand_length * math.sin(hour_angle) + CENTER,
        hour_hand_tail_length * math.cos(reversed_hour_angle) + CENTER,
        hour_hand_tail_length * math.sin(reversed_hour_angle) + CENTER,
    )

    # 分針の移動
    canvas.coords(
        minute_hand,
        minute_hand_length * math.cos(minute_angle) + CENTER,
        minute_hand_length * math.sin(minute_angle) + CENTER,
        minute_hand_tail_length * math.cos(reversed_minute_angle) + CENTER,
        minute_hand_tail_length * math.sin(reversed_minute_angle) + CENTER,
    )

    # 秒針の移動
    canvas.coords(
        second_hand,
        second_hand_length * math.cos(second_angle) + CENTER,
        second_hand_length * math.sin(second_angle) + CENTER,
        second_hand_tail_length * math.cos(reversed_second_angle) + CENTER,
        second_hand_tail_length * math.sin(reversed_second_angle) + CENTER,
    )

前の行で既にhour_angleが弧度法になっています。

そのため、度数法の\(180°\)の代わりに弧度法の\(\pi\)で引いている点にご注意ください。

    # 針の角度と逆向きの角度
    reversed_hour_angle = hour_angle - math.pi
    reversed_minute_angle = minute_angle - math.pi
    reversed_second_angle = second_angle - math.pi

垢抜けたと感じるか、逆に間延びしたと思うかは、人によりそうです。

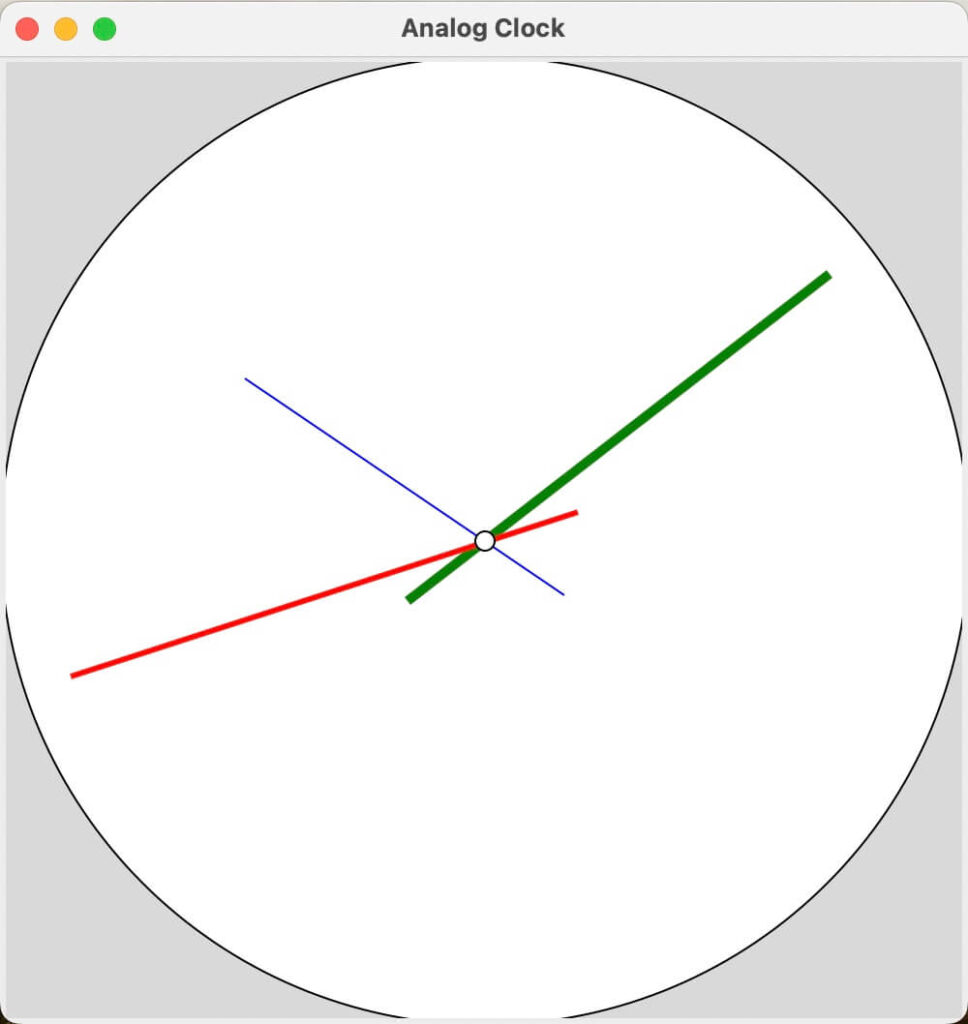
針の形状

現在\(3\)つの針はすべて線分で描いていますが、多角形で描画すると複雑な形状にできます。

例えば、針の形をこのような四角形にしてみましょう。

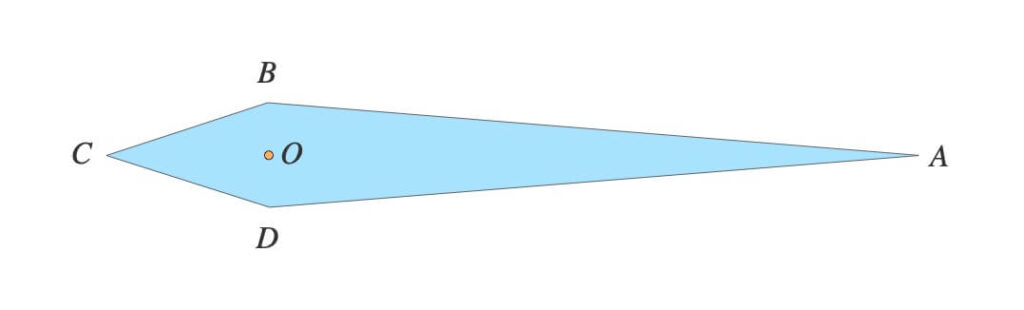
\(A\)は針先、\(C\)は針の尻尾で、\(O\)は時計盤の中心です。

\(A\)・\(C\)の座標は既に導出済みですから、問題は左右の\(B\)・\(D\)の座標です。

結論を述べると、\(B\)・\(D\)の座標は次で与えられます。

針の左右の座標

\(x\)座標:　\((針の幅 / 2) × \cos{(針の角度 \mp 90°)} + 時計の中心のx座標\)
\(y\)座標:　\((針の幅 / 2) × \cos{(針の角度 \mp 90°)} + 時計の中心のy座標\)

先生

\(B\)が\(-90°\)で\(D\)が\(+90°\)の式です。

座標の求め方を解説します。

線分\(AC\)は針の中心線であり、まさに今まで針として描画してきた線分です。

直線\(BD\)と線分\(AC\)は直角に交わります。

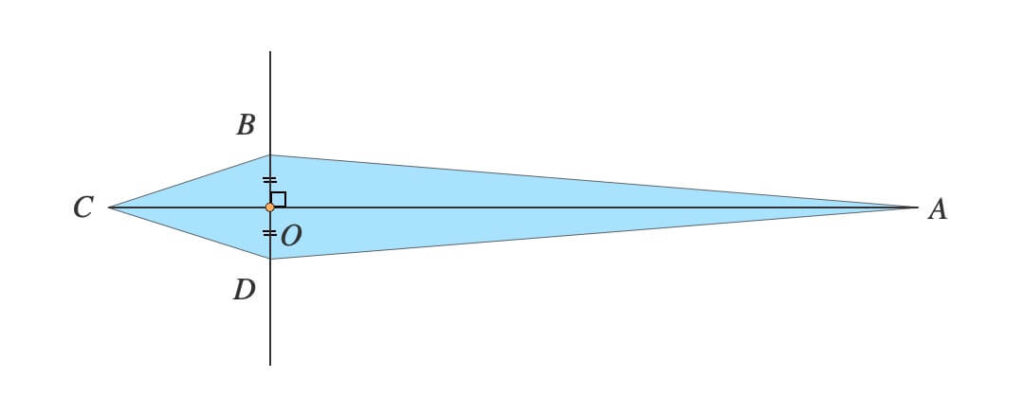
つまり、線分\(AC\)の傾き\(\mp 90°\)で直線\(BD\)の傾きになります。

現在時刻から線分\(AC\)の傾き(針の角度)は、計算式で分かるんでしたね。

したがって、直線\(BD\)の角度(針の角度\(\mp 90°\))と針の幅\(BD\)の半分より、\(B\)・\(D\)の座標がこうなるのです。

針の左右の座標

\(x\)座標:　\((針の幅 / 2) × \cos{(針の角度 \mp 90°)} + 時計の中心のx座標\)
\(y\)座標:　\((針の幅 / 2) × \cos{(針の角度 \mp 90°)} + 時計の中心のy座標\)

ちょうど針の角度と長さから、針の先端の座標を求めたのと同じ容量です。

ここからコードを修正していきます。

まず、針をcreate_lineメソッドではなく、create_polygonメソッドで描きます。

四角形なので、頂点の数は\(x\)座標と\(y\)座標を合わせて\(8\)つです。

# 時針の作成
hour_hand = canvas.create_polygon(
    0, 0, 0, 0, 0, 0, 0, 0,
    fill="blue",
    outline="black",
)

# 分針の作成
minute_hand = canvas.create_polygon(
    0, 0, 0, 0, 0, 0, 0, 0,
    fill="green",
    outline="black",
)

# 秒針の作成
second_hand = canvas.create_polygon(
    0, 0, 0, 0, 0, 0, 0, 0,
    fill="red",
    outline="black",
)

座標はtick関数内で計算するので、ここでは適当で構いません。

さらにtick関数の座標計算の箇所を書き換えます。

coordsメソッドに\(A\)→\(B\)→\(C\)→\(D\)の順に座標を渡しています。

    # 針の膨らみ
    hour_hand_width_half = CLOCK_FACE_RADIUS * 0.05
    minute_hand_width_half = CLOCK_FACE_RADIUS * 0.05
    second_hand_width_half = CLOCK_FACE_RADIUS * 0.025

    # 時針の移動
    canvas.coords(
        hour_hand,
        hour_hand_length * math.cos(hour_angle) + CENTER,
        hour_hand_length * math.sin(hour_angle) + CENTER,
        hour_hand_width_half * math.cos(hour_angle - math.pi / 2) + CENTER,
        hour_hand_width_half * math.sin(hour_angle - math.pi / 2) + CENTER,
        hour_hand_tail_length * math.cos(reversed_hour_angle) + CENTER,
        hour_hand_tail_length * math.sin(reversed_hour_angle) + CENTER,
        hour_hand_width_half * math.cos(hour_angle + math.pi / 2) + CENTER,
        hour_hand_width_half * math.sin(hour_angle + math.pi / 2) + CENTER,
    )

    # 分針の移動
    canvas.coords(
        minute_hand,
        minute_hand_length * math.cos(minute_angle) + CENTER,
        minute_hand_length * math.sin(minute_angle) + CENTER,
        minute_hand_width_half * math.cos(minute_angle - math.pi / 2) + CENTER,
        minute_hand_width_half * math.sin(minute_angle - math.pi / 2) + CENTER,
        minute_hand_tail_length * math.cos(reversed_minute_angle) + CENTER,
        minute_hand_tail_length * math.sin(reversed_minute_angle) + CENTER,
        minute_hand_width_half * math.cos(minute_angle + math.pi / 2) + CENTER,
        minute_hand_width_half * math.sin(minute_angle + math.pi / 2) + CENTER,
    )

    # 秒針の移動
    canvas.coords(
        second_hand,
        second_hand_length * math.cos(second_angle) + CENTER,
        second_hand_length * math.sin(second_angle) + CENTER,
        second_hand_width_half * math.cos(second_angle - math.pi / 2) + CENTER,
        second_hand_width_half * math.sin(second_angle - math.pi / 2) + CENTER,
        second_hand_tail_length * math.cos(reversed_second_angle) + CENTER,
        second_hand_tail_length * math.sin(reversed_second_angle) + CENTER,
        second_hand_width_half * math.cos(second_angle + math.pi / 2) + CENTER,
        second_hand_width_half * math.sin(second_angle + math.pi / 2) + CENTER,
    )

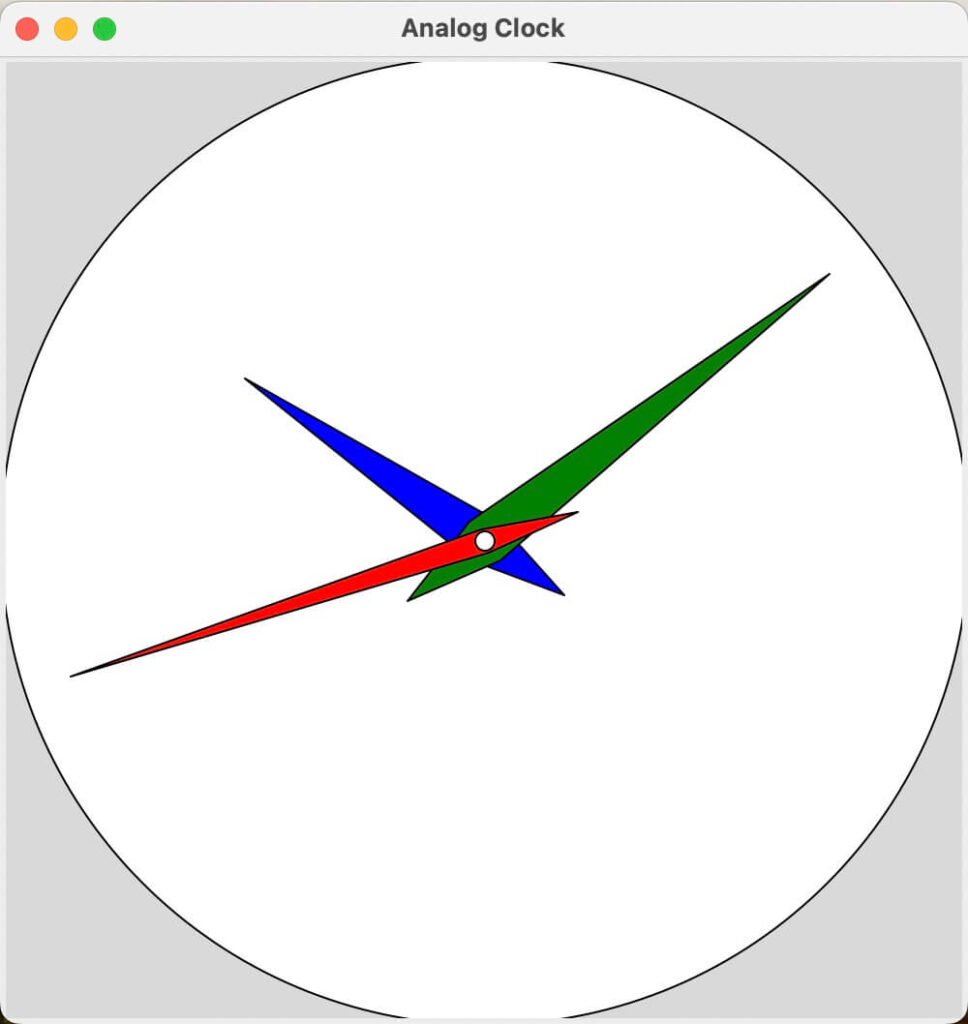
関数化を検討するレベルですが、ご容赦を。

刺されたら痛そうです。