- ユークリッドの互除法の原理
- Binary GCD Algorithm(バイナリ・ユークリッドの互除法)の原理
- \(2\)数の最大公約数を求めるプログラム
こんにちは、Youta(@youta_blog)です。
今回は、最大公約数を求めるお話です。

部屋の模様替えで、床一面にタイル敷くよー。
でもだるいから、極力最低限の枚数だけにしたいなー。

素敵ですね。
最大公約数を利用すると、必要なタイルの枚数がわかりますよ。
すずかさんの部屋の間取りを元に、こんな問題を作ってみました。
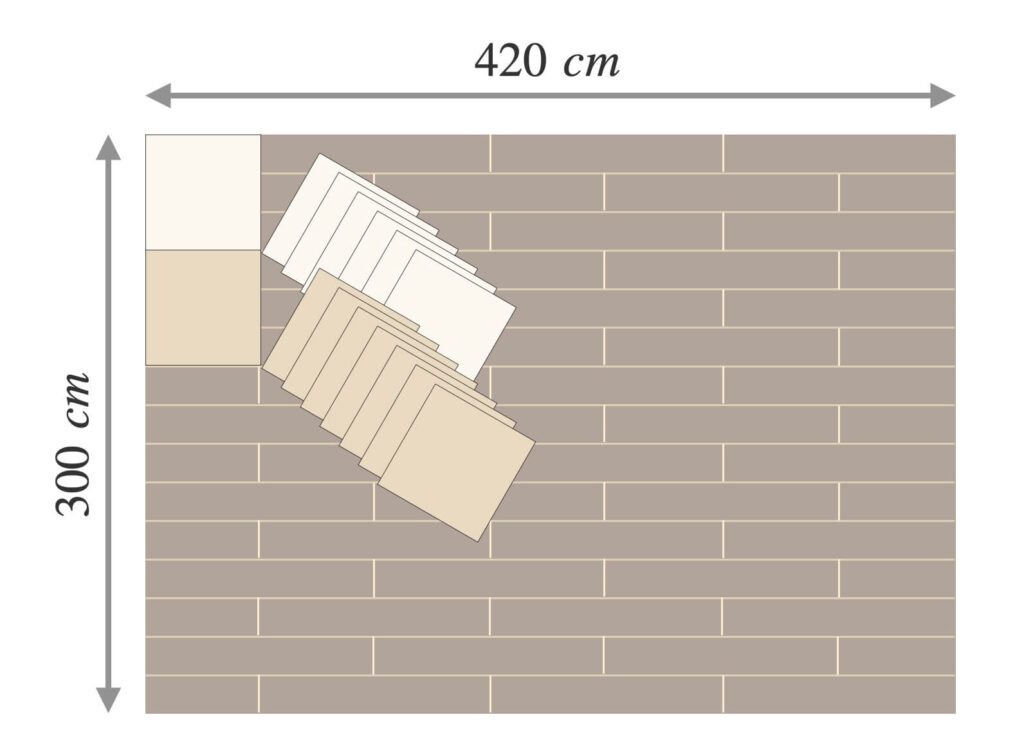
縦\(300\ cm\)、横\(420\ cm\)の床を、可能な限り大きな正方形のタイルで敷き詰める。
\((1)\) タイルの一辺の長さは何\(cm\)か。
\((2)\) タイルの枚数を求めよ。
実はこの問題、最大公約数が深く関わっています。
本記事を読めば、この問題の対処法を学べます。
また、最大公約数を求める有名なアルゴリズム・証明を解説します。
さらには、コンピュータで自動で最大公約数を求めるプログラムもご紹介します。
最大公約数の利用
まず始めに、冒頭の問題の答えを示します。

\((1)\) \(60\ cm\)
\((2)\) \(35\)枚

どうやって求めたん?
最大公約数が必要な理由
実は\((1)\)の答え\(60\)は、縦の長さ\(300\)と横の長さ\(420\)の最大公約数です。

なぜに最大公約数?
例えば、タイル張りが苦でない人は一辺\(10\ cm\)のタイルを床に敷こうとするでしょう。
縦に\(30\)個、横に\(42\)個のタイルを敷けばピッタリです。
しかし、タイルの予算や労力を考えると現実的ではないですよね。

じゃあ一辺\(100\ cm\)とかでやれば良いじゃん。

言いましたね?やりますよ?
はい、タイルの枚数が\(12\)枚ですので作業が楽になりました。
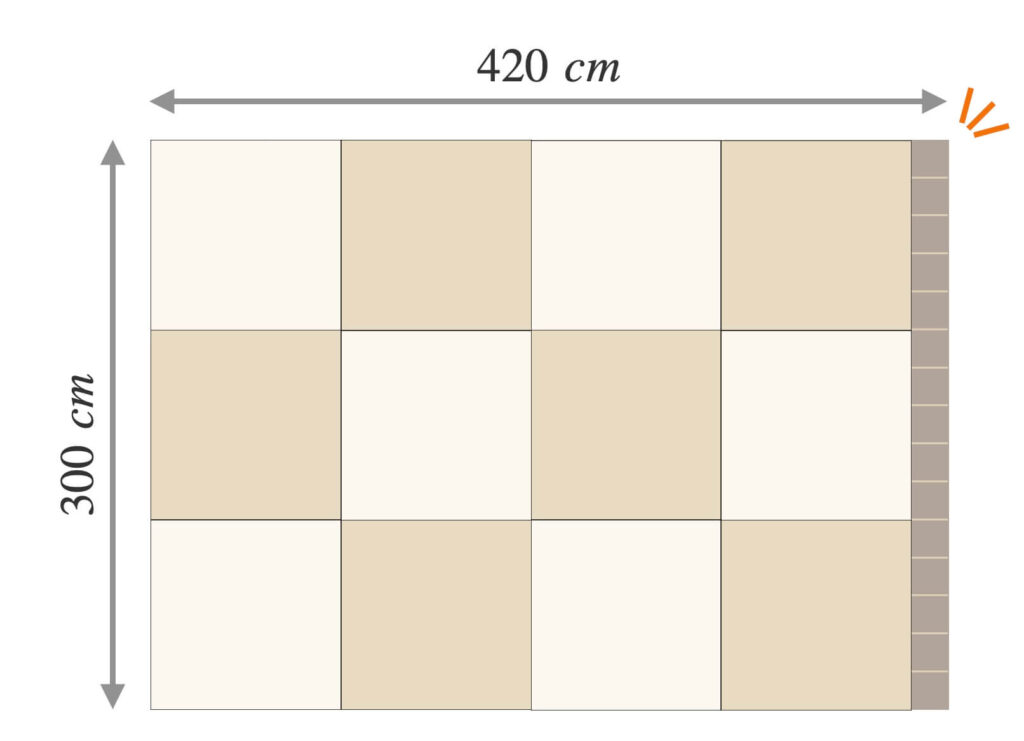
ですが、余った部分が発生しました。
どうやら、適当なサイズではタイルを床にピッタリと敷き詰められないことがわかります。
そこで、隙間なく敷き詰めるために約数を考えなければならないのです。

いや流石に約数は知ってるけど、なんで?
仮に床をタイルで隙間なく敷き詰められたときを考えましょう。
下図は、先ほどの一辺\(10\ cm\)のタイルの例です。
縦に\(30\)個、横に\(42\)個のタイルが敷かれているのでしたね。

このとき、縦の長さ\(=\)タイルの一辺\(×\)縦に並ぶタイルの枚数です。
\(300 = 10 × 30\)ですからね。
同様に、横の長さ\(=\)タイルの一辺\(×\)横に並ぶタイルの枚数です。
\(420 = 10 × 42\)ですから。
つまり、床をタイルで完全に敷き詰めたとき、タイルの一辺は縦横の長さの公約数です。
一辺\(100\ cm\)のタイルで失敗するのは、\(100\)が\(300\)と\(420\)の公約数ではないからです。
実際に\(420=100×4+20\)ですから、横に\(20\ cm\)の余りが生じます。

\(2\)数の公約数を見つけることは、
その\(2\)数を辺とする長方形に、ピッタリ敷き詰められる正方形の一辺を探すのと同じです。
したがって、タイルの一辺の候補は、\(300\)と\(420\)の公約数です。
そして一番大きなタイルの一辺とは、公約数の最大値、つまり最大公約数ですね。
次章では、\(300\)と\(420\)の最大公約数を求める方法を解説します。
\(2\)数の最大公約数の視覚的理解
\(300\)と\(420\)の最大公約数を求めます。
素因数分解を使っても良いですが、ここでは図形的に最大公約数を求めてみましょう。
結論、取り敢えず面積が許す限りの巨大なタイルを順に敷き詰めていきます。
「もうタイルを敷けない!」となるときのタイルの一辺が、\(300\)と\(420\)の最大公約数です。
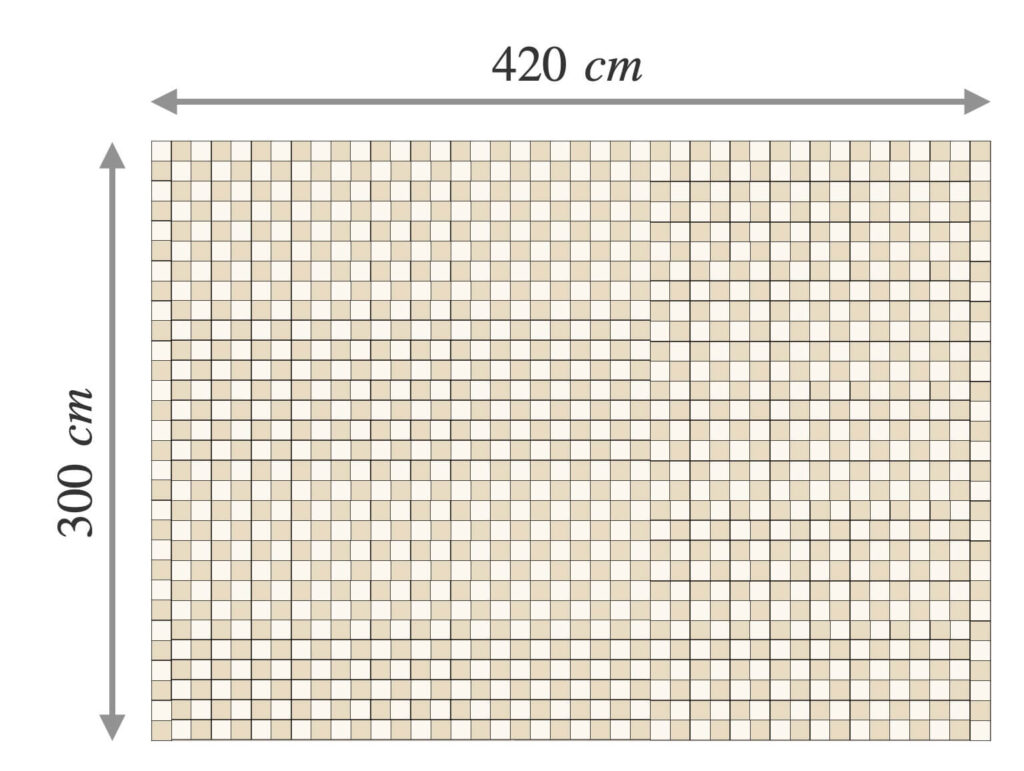
まず、一辺\(300\ cm\)のタイルを床に敷きます。
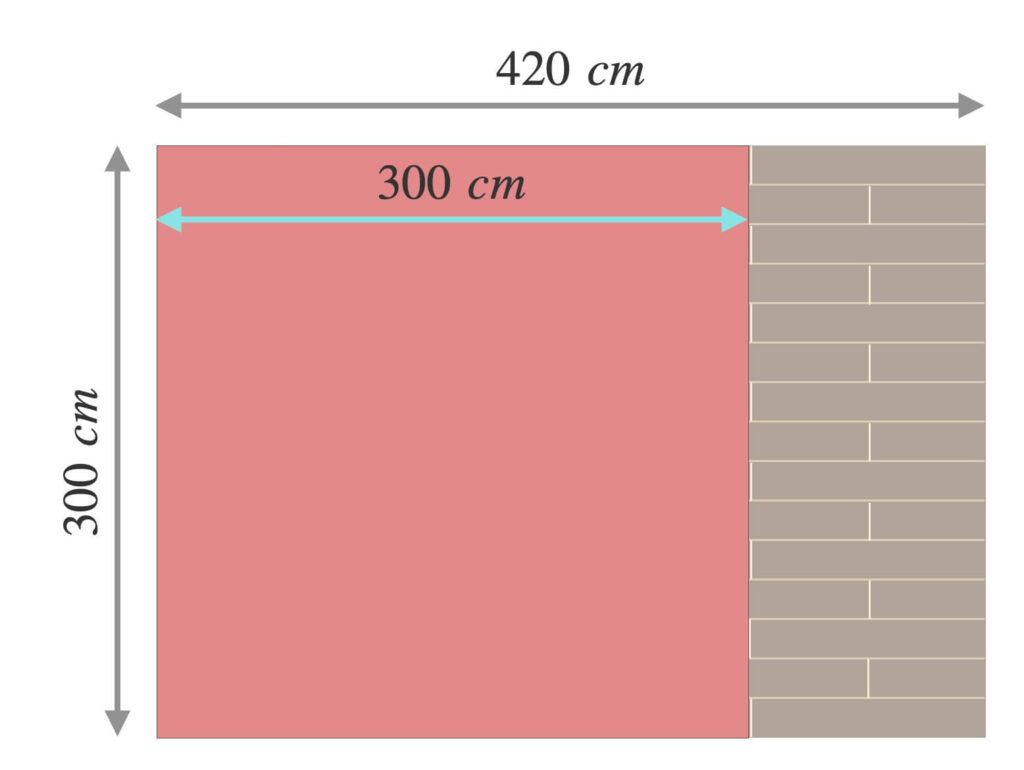
さらに、余った領域に一辺\(120\ cm\)のタイルを敷きます。
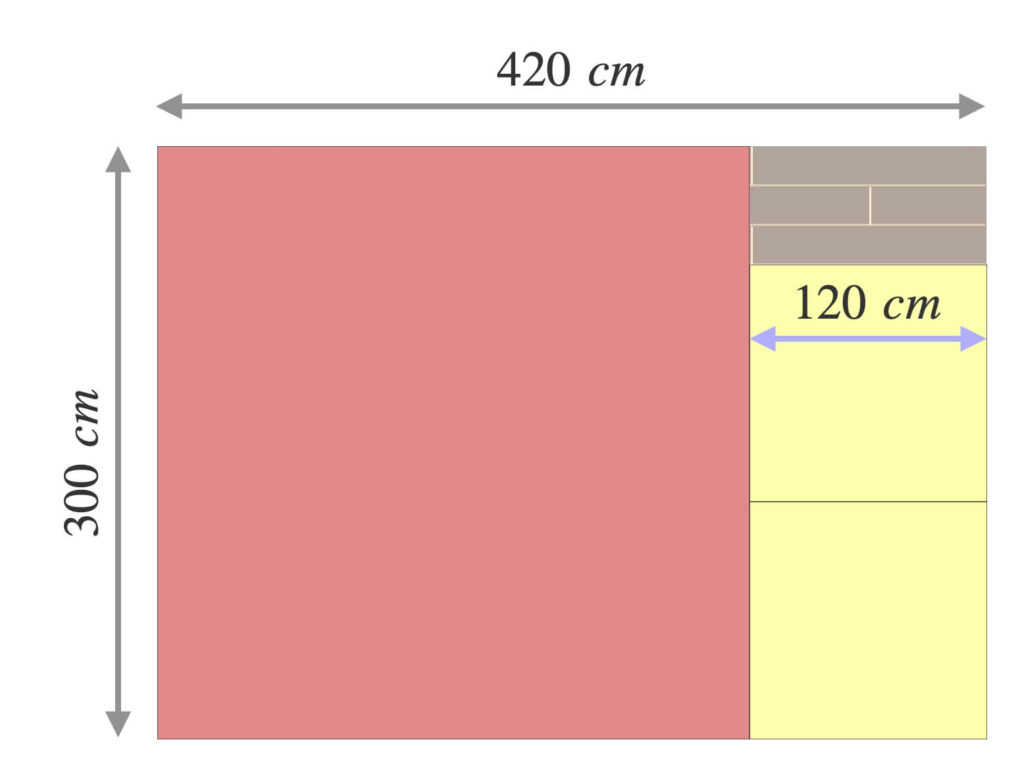
一辺\(60\ cm\)のタイルを\(2\)枚敷き、とうとう床が見えなくなりました。
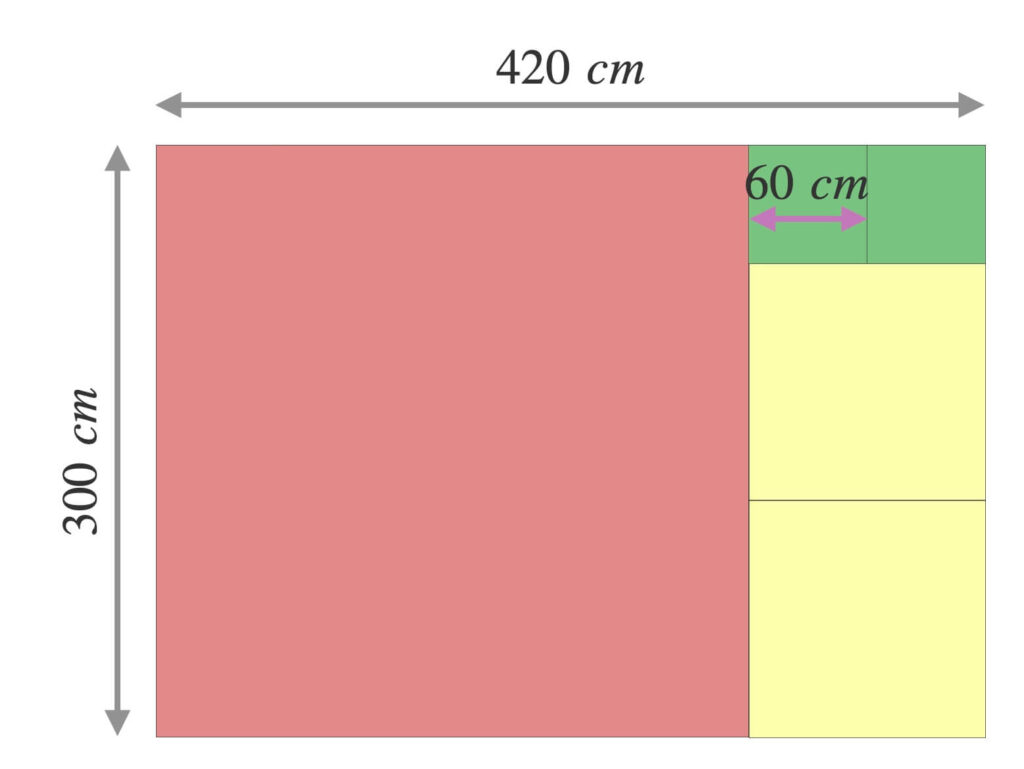

だからなんなの?

面白いのはこれからです。
今度は逆に、小さな視点から大きな視点に変えていきますよ。
\(60\)と\(120\)の最大公約数は\(60\)です。
ゆえに、一辺\(60\ cm\)の緑のタイルで一辺\(120\ cm\)の黄色のタイルを隙間なく埋められます。
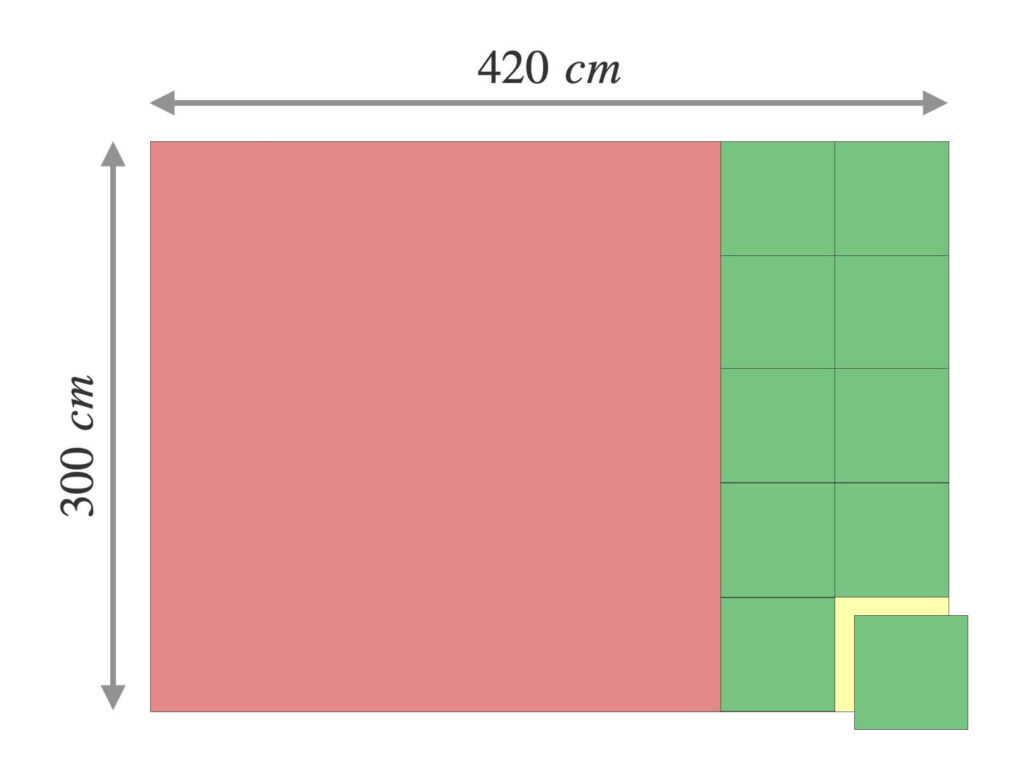
また、\(120\)と\(300\)の最大公約数も\(60\)です。
よって、一辺\(60\ cm\)の緑のタイルで一辺\(300\ cm\)の赤のタイルも隙間なく埋められます。
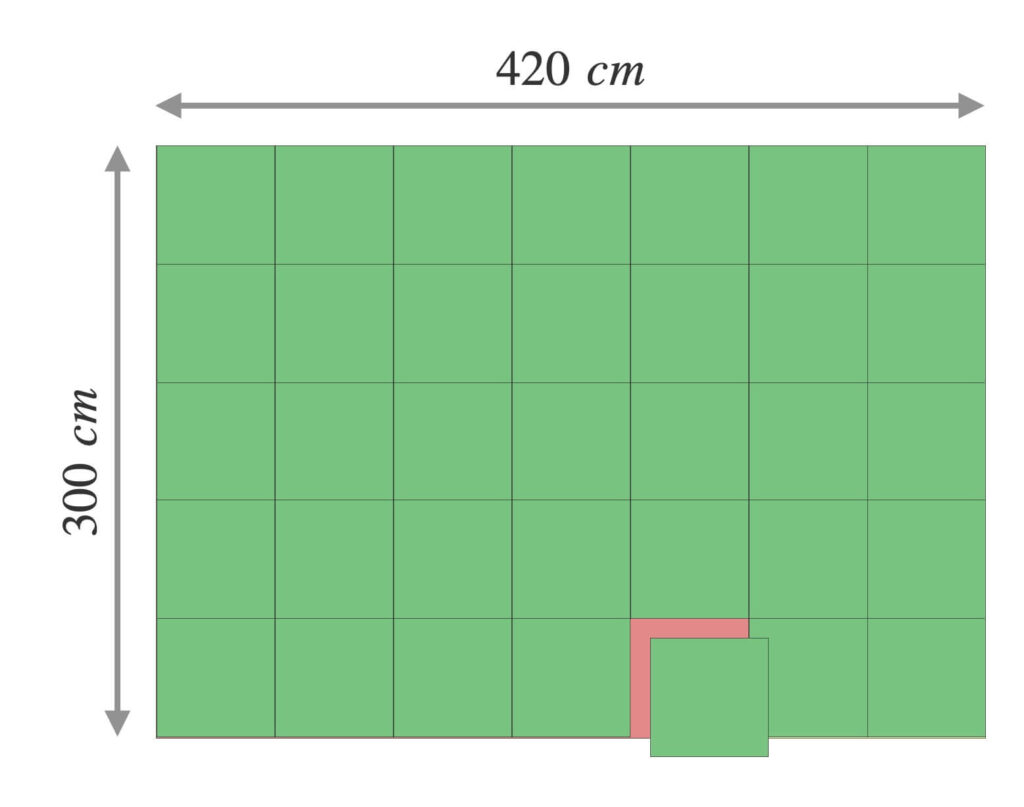
床が一辺\(60\ cm\)の緑のタイルでピッタリ埋まるので、\(60\)は\(300\)と\(420\)の公約数です。
また、できる限り大きなタイルから順に敷いていったので、
一辺\(60\ cm\)の緑のタイルもできる限り大きいはずです。
したがって、\(60\)が\(300\)と\(420\)の最大公約数となり、求める数値となるのです。
最後に、タイルの枚数を求めて問題を締め括りましょう。
縦には\(300÷60\)で\(5\)枚並んでおり、横には\(420÷60\)で\(7\)枚並んでいます。
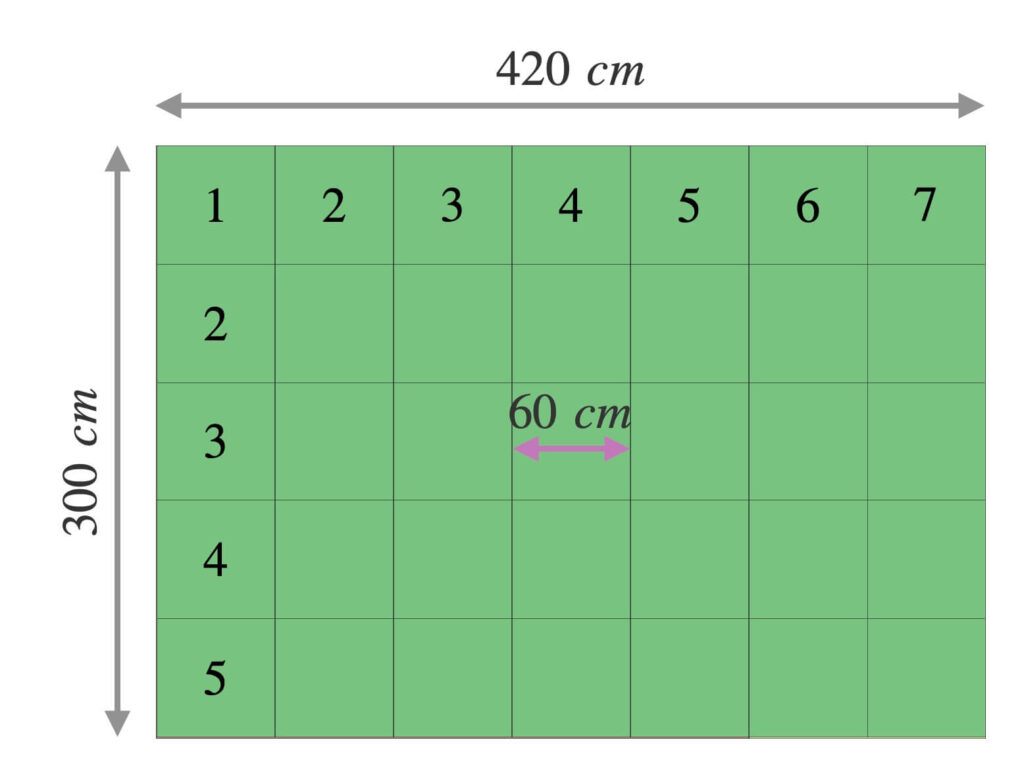
したがって、\(5×7\)でタイルの枚数は\(35\)枚です。
\((1)\) \(60\ cm\)
\((2)\) \(35\)枚
ユークリッドの互除法
先ほどは、視覚的に最大公約数を求めました。
ですが、実際やった手順はユークリッドの互除法そのものです。
ユークリッドの互除法とは、2つの整数の最大公約数を求めるアルゴリズムです。
次のプロセスにより、最大公約数が求まります。
自然数\(a\)と\(b\)\((a\ge b)\)の最大公約数を求める。
- \(b=0\)ならば、\(a\)を最大公約数としてアルゴリズムを終了する。
- \(a\)を\(b\)で割った余り\(r\)を求める。
- \(a=b\)、\(b=r\)として①に戻る。
これは、古代ギリシアの数学者ユークリッドの発見による最大公約数を求める手法です。

具体例で説明しましょう。
具体例
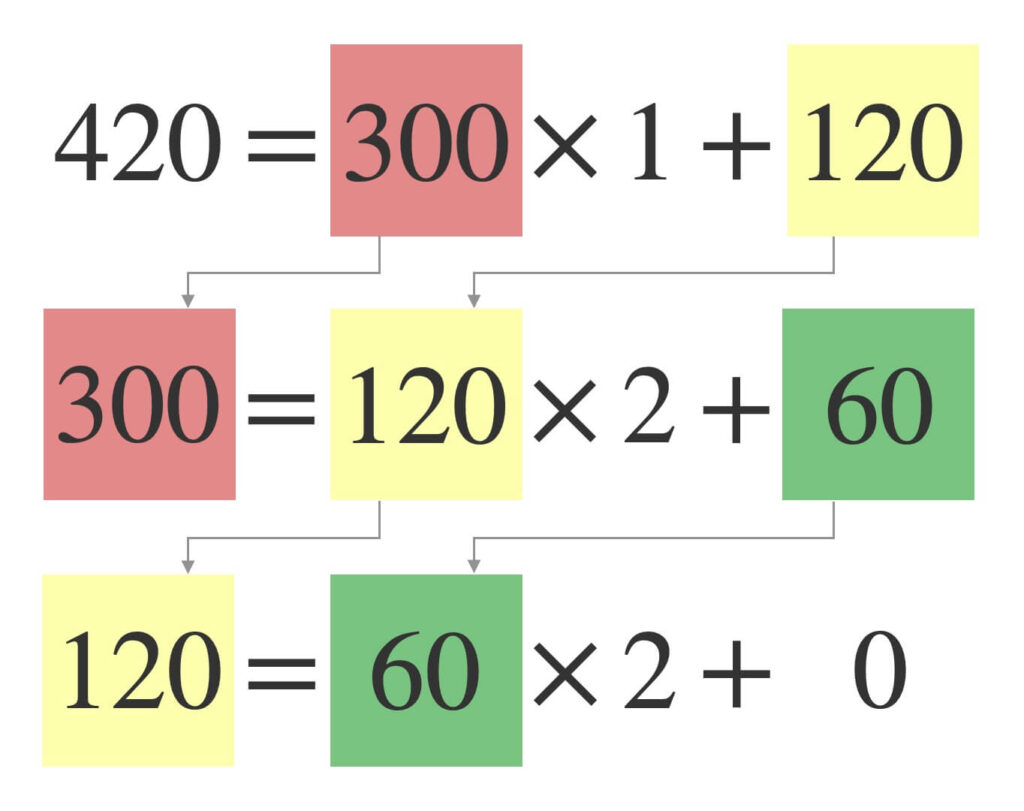
\(a = 420\)と\(b = 420\)の最大公約数をユークリッドの互除法で求めます。
上図の\(3\)本の計算式を順に解説します。
②より、\(a = 420\)を\(b = 300\)で割った余り\(r = 120\)を求めます。
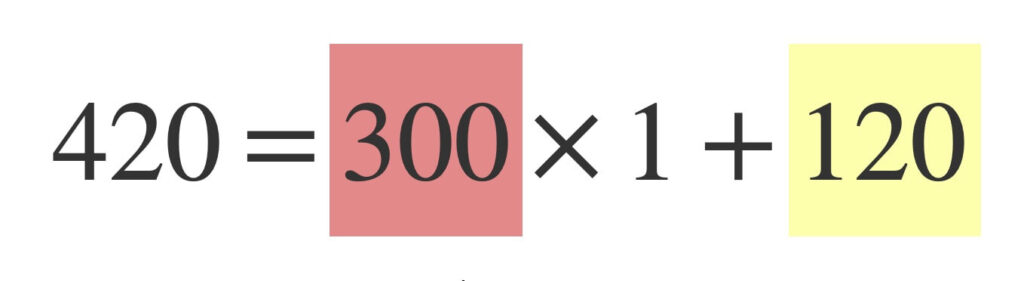
\(300H×420W\)の長方形に一辺\(300\)のタイルを\(1\)つ敷くと、横に\(120\)余る状態です。
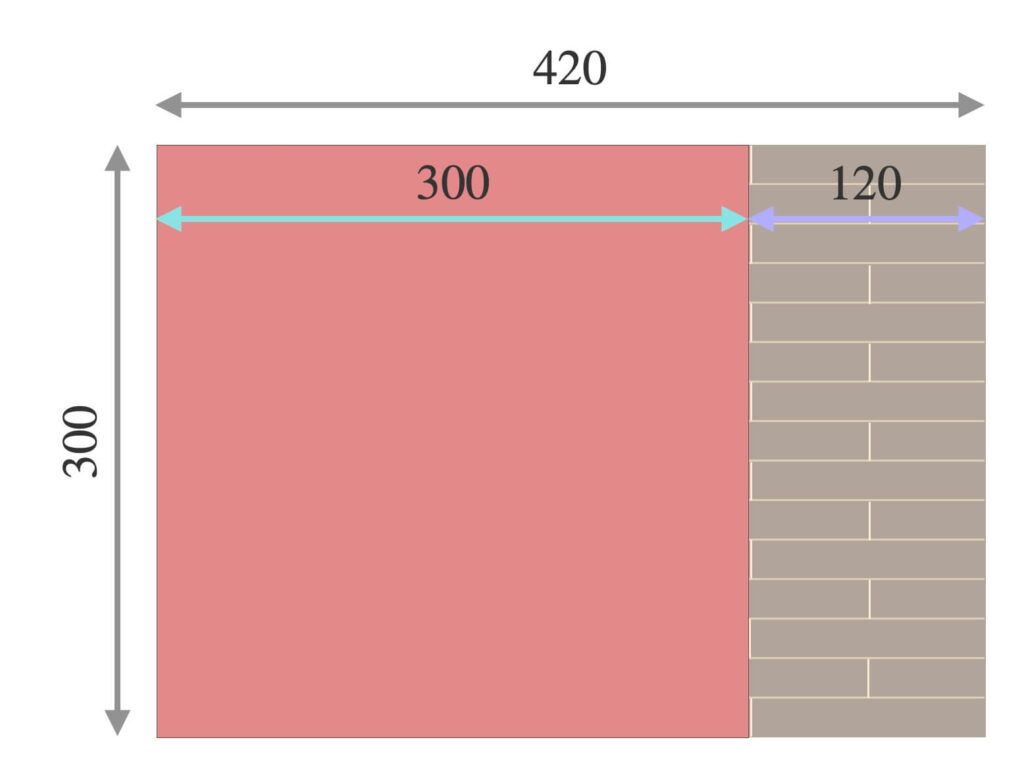
現時点で\(a = 420\)と\(b = 300\)と\(r = 120\)ですね。
しかし、③より新たに\(a = b\)、\(b = r\)とします。
そして、次は\(a = 300\)と\(b = 120\)の最大公約数を求めるのです。
②より、\(a = 300\)を\(b = 120\)で割った余り\(r = 60\)を求めます。
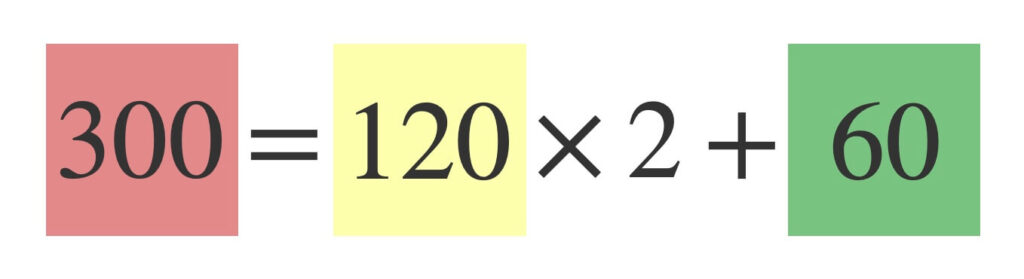
\(300H×120W\)の長方形に一辺\(120\)のタイルを\(2\)つ敷くと、縦に\(60\)余る状態です。
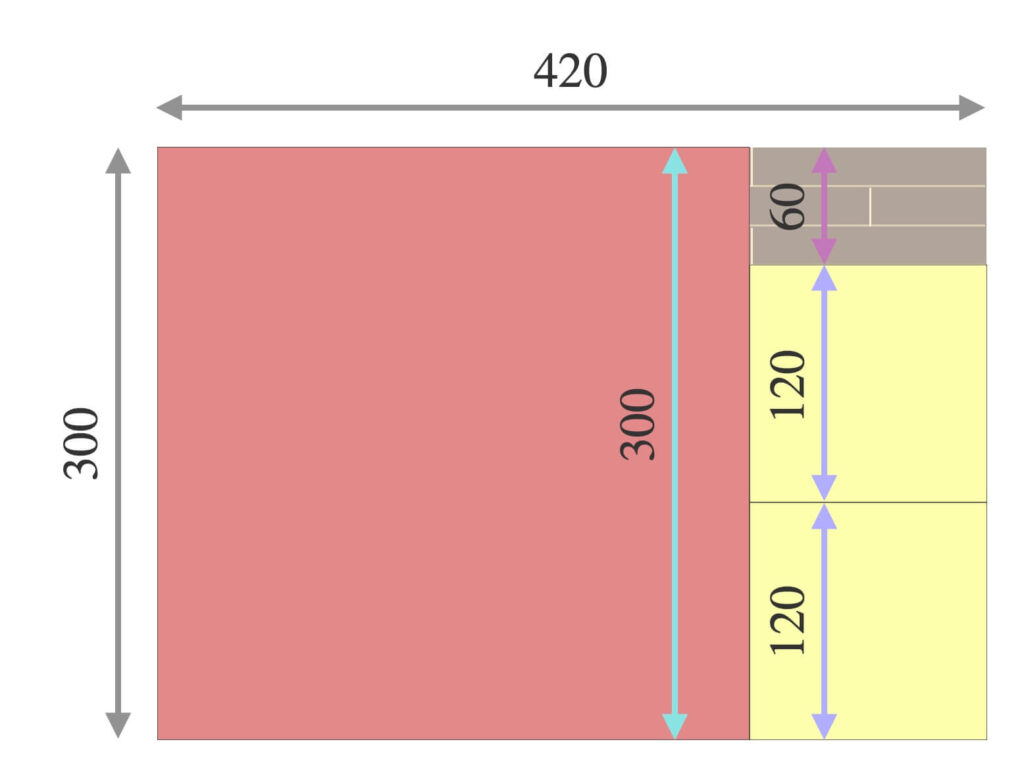
現時点で\(a = 300\)と\(b = 120\)と\(r = 60\)ですね。
しかし、③より新たに\(a = b\)、\(b = r\)とします。
そして、次は\(a = 120\)と\(b = 60\)の最大公約数を求めるのです。
②より、\(a = 120\)を\(b = 60\)で割った余り\(r = 0\)を求めます。
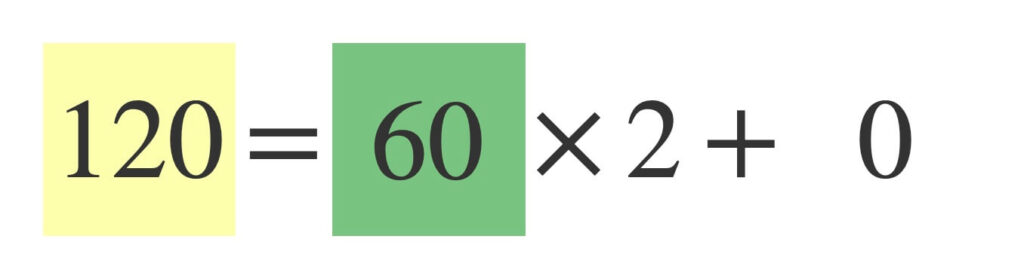
\(60H×120W\)の長方形に一辺\(60\)のタイルを\(2\)つ敷くと、余りが生じない状態です。
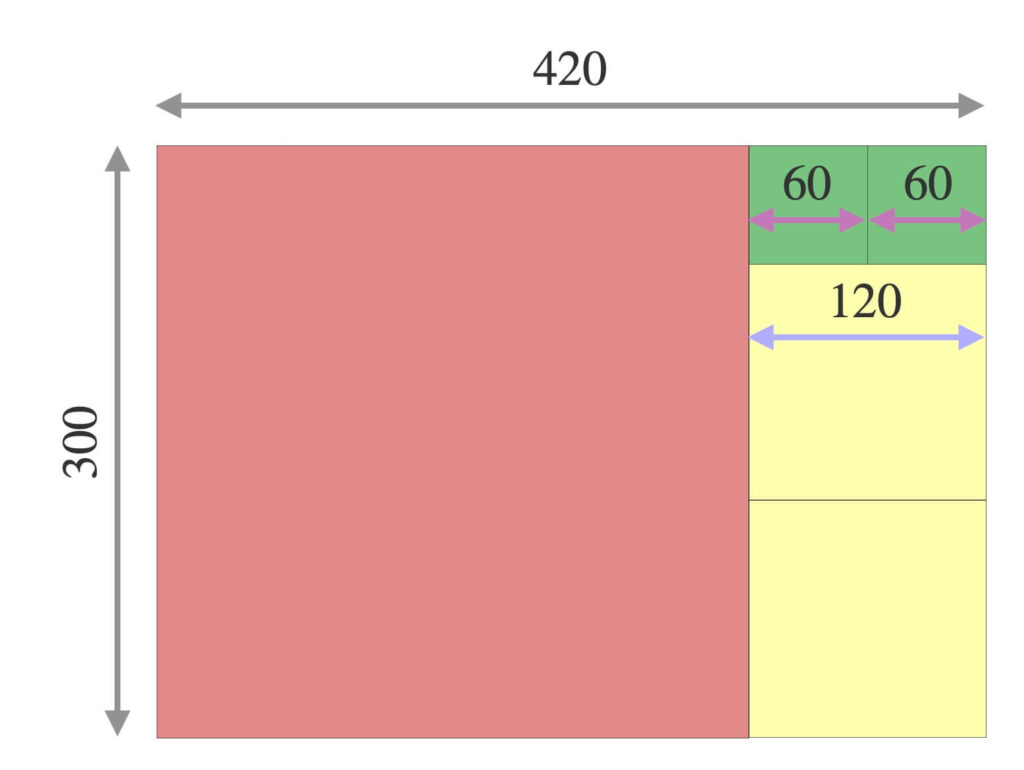
現時点で\(a = 120\)と\(b = 60\)と\(r = 0\)ですね。
しかし、③より新たに\(a = b\)、\(b = r\)とします。
そして、次は\(a = 60\)と\(b = 0\)の最大公約数を求めるのです。
と言いたいところですが、①より\(b = 0\)のときは\(a = 60\)を最大公約数とするのでした。
つまり、この\(60\)こそが元の\(420\)と\(300\)の最大公約数です。
ユークリッドの互除法の強みは、最大公約数を求めたい\(2\)数を徐々に小さくすることです。
今回は\(420\)と\(300\)の最大公約数 = \(300\)と\(120\)の最大公約数 = \(120\)と\(60\)の最大公約数 でした。
\(420\)と\(300\)の最大公約数を求める代わりに、\(120\)と\(60\)の最大公約数を求めれば良いのです。
よって、どんなに巨大な数同士でも、必ず有限回の操作で最大公約数を求められます。
とはいえ、多くの方が疑問に思ったはずです。
なぜ、割られる数と割る数の最大公約数 = 割る数と余りの最大公約数なのか。
次はこの理由について解説します。
証明
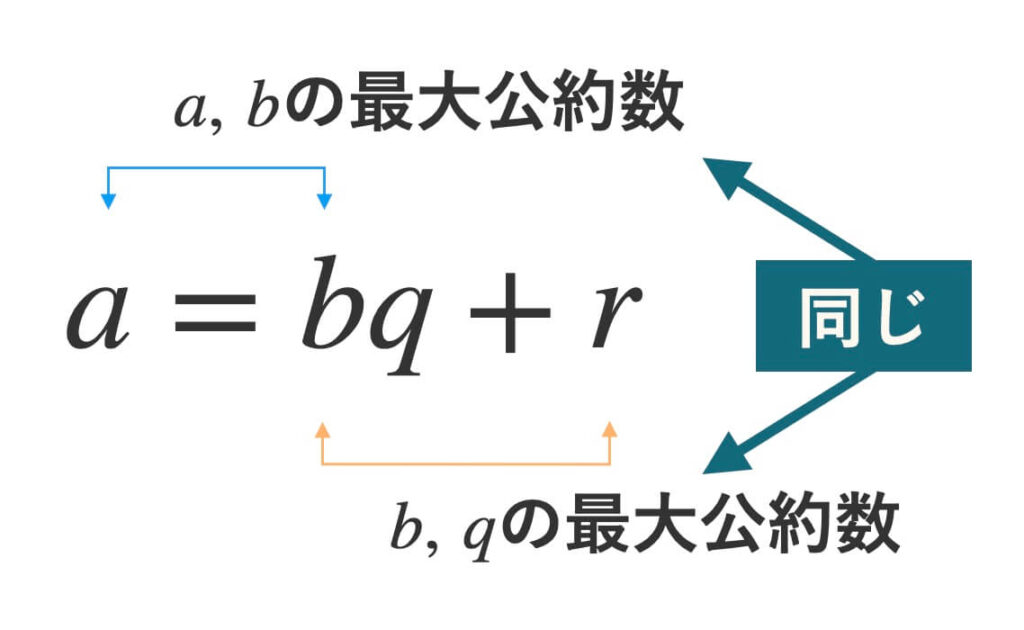
ユークリッドの互除法は、以下の数学的事実に立脚します。
自然数\(a\)と\(b\)について、\(a\)を\(b\)で割ったときの余りを\(r\)とする。
このとき、\(a\)と\(b\)の最大公約数は、\(b\)と\(r\)の最大公約数に等しい。
以降、\(a\)と\(b\)の最大公約数を\(\gcd{(a, b)}\)と表記することにします。

\(\gcd{}\)とは、最大公約数の英訳・greatest common divisorの略です。
\(g = \gcd{(a, b)}\)、\(g’ = \gcd{(b, r)}\)として、\(g = g’\)を示します。
\(g =\gcd{(a, b)}\)より、\(a = ga’\)と\(b = gb’\)が従います。・・・①
ただし、\(a’\)と\(b’\)は互いに素な自然数です。
仮定より、\(a = bq + r \iff r = a – bq\)
①より、\(r = a – bq = ga’ – gb’q = g(a’ – b’q)\)
\(a’ – b’q\)は整数ですから、\(g\)は\(r\)の約数です。
また、①より\(g\)は\(b\)の約数でもあるので、\(g\)は\(b\)と\(r\)の公約数です。
\(g’ = \gcd{(b, r)}\)なので、\(g ≦ g’\)・・・②
\(g’ = \gcd{(b, r)}\)より、\(b = g’b”\)と\(r = g’r’\)が従います。・・・③
ただし、\(b”\)と\(r’\)は互いに素な自然数です。
仮定と③より、
\(a = bq + r = g’b”q + g’r’ = g'(b”q + r’)\)
\(b”q + r’\)は整数ですから、\(g’\)は\(a\)の約数です。
また、③より\(g’\)は\(b\)の約数でもあるので、\(g’\)は\(a\)と\(b\)の公約数です。
\(g = \gcd{(a, b)}\)なので、\(g’ ≦ g\)・・・④
③と④より、\(g ≦ g’\)かつ\(g’ ≦ g\)であるから\(g = g’\)
プログラム
ユークリッドの互除法を用いて、最大公約数を求めるPythonプログラムの例です。
def euclidean_gcd(a, b):
a, b = abs(a), abs(b)
while b:
a, b = b, a % b
return aユークリッドの互除法のアルゴリズムをeuclidean_gcd 関数で実装しました。
\(2\)つの整数を入力し、それらの最大公約数を計算します。
実行例です。
num1 = 527
num2 = 341
result = euclidean_gcd(num1, num2)
print(result)
# 31whileループは、bがTrue(\(\ne 0\))である限り、繰り返し処理を行います。
言い換えると、bが\(0\)になるとループを抜けます。
while b:ユークリッドの互除法は b が\(0\)になったときに終わりますよね。
ここでは、変数の入れ替えを行なっています。
a, b = b, a % ba は今のb の値に置き換えられます。
また、bは aを bで割った余り(a % b)に置換されます。
Binary GCD Algorithm (Stein’s Algorithm)
この章だけはハイレベルなので、本職のエンジニアの方向けになります。
興味がある方は、雰囲気だけでも一緒に楽しみましょう!
先ほどは、ユークリッドの互除法を紹介しました。
実は、もう一つ有名な最大公約数を求めるアルゴリズムが存在します。
それが、Binary GCD Algorithm(以下「バイナリ・ユークリッドの互除法」)です。
自然数\(a\)と\(b\)の最大公約数を求める。
- \(a=0\)ならば、\(\gcd{(a,b)}=b\)とする。\(a\)と\(b\)が逆でも同様。
- \(a\)も\(b\)も偶数ならば、\(\gcd{(a,b)}=2 \gcd{(\frac{a}{2}, \frac{b}{2})}\)とする。
- \(a\)のみが偶数ならば、\(\gcd{(a,b)}=\gcd{(\frac{a}{2},b)}\)とする。\(a\)と\(b\)が逆でも同様。
- \(a\)も\(b\)も奇数ならば、\(\gcd{(a,b)}=\gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\)とする。
表にするとこんな感じです。
| \(a\) | \(b\) | \(\gcd{(a, b)}\) | 備考 |
|---|---|---|---|
| \(a\) | 0 | \(a\) | \(a\)と\(b\)が逆でも同様。 |
| 偶数 | 偶数 | \(2 \gcd{(\frac{a}{2}, \frac{b}{2})}\) | |
| 偶数 | 奇数 | \(\gcd{(\frac{a}{2},b)}\) | \(a\)と\(b\)が逆でも同様。 |
| 奇数 | 奇数 | \(\gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\) |
※ \(\min{(a, b)}\)は\(a\)と\(b\)のどちらか小さい方。
ユークリッドの互除法とほぼ同時期に中国で発見されたと言われるアルゴリズムです。
\(1967\)年にイスラエルの学者・ジョセフ=シュタインさんに再発見されました。
コンピューターが得意な\(2\)の除算を数多く取り入れ、高速化を試みている点が特徴です。
具体例

\(a = 18\)と\(b = 12\)の最大公約数をバイナリ・ユークリッドの互除法で求めます。
上図の\(5\)本の計算式を順に解説します。
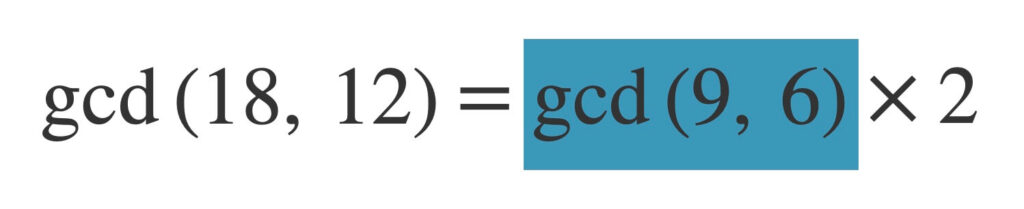
\(a = 18\)と\(b = 12\)では、\(a\)も\(b\)も偶数です。
②より
\(\gcd{(a, b)}=2\gcd{(\frac{a}{2}, \frac{b}{2})}=2\gcd{(\frac{18}{2}, \frac{12}{2})}=2\gcd{(9, 6)}\)
このとき、共通因数として\(2\)を保存しておきます。・・・★
先に\(\gcd{(9,6)}\)を求めて、最後に\(2\)を掛け合わせる流れです。
ここまでは\(a = 18\)、\(b = 12\)でしたが、新たに\(a = 9\)、\(b = 6\)として次に進みます。
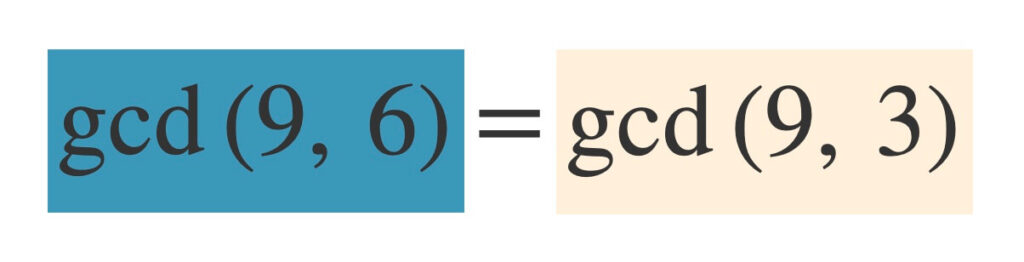
\(a = 9\)と\(b = 6\)では、\(a\)が奇数で\(b\)が偶数です。
③より
\(\gcd{(a, b)}=\gcd{(a, \frac{b}{2})}=\gcd{(9, \frac{6}{2})}=\gcd{(9, 3)}\)
ここまでは\(a = 9\)、\(b = 6\)でしたが、新たに\(a = 9\)、\(b = 3\)として次に進みます。
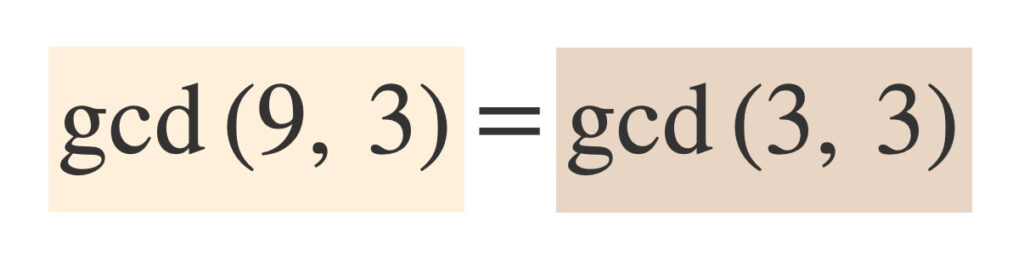
\(a = 9\)と\(b = 3\)では、\(a\)も\(b\)も奇数です。
④より
\(\gcd{(a, b)}=\gcd{(\frac{|a-b|}{2}, \min{(a, b)}})=\gcd{(\frac{|9-3|}{2}, \min{(9, 3)}})=\gcd{(3, 3)}\)
ここまでは\(a = 9\)、\(b = 3\)でしたが、新たに\(a = 3\)、\(b = 3\)として次に進みます。
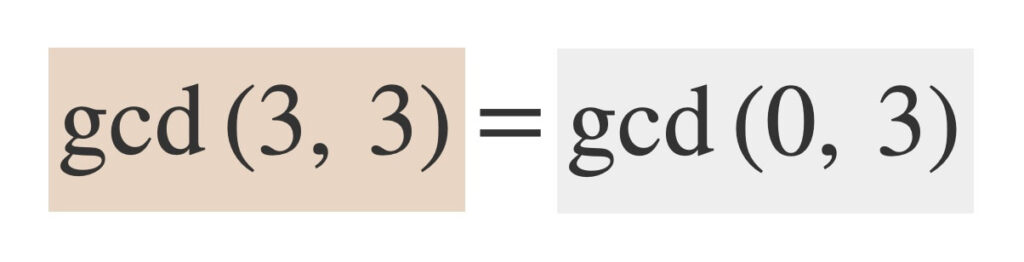
\(a = 3\)と\(b = 3\)では、\(a\)も\(b\)も奇数です。
④より
\(\gcd{(a, b)}=\gcd{(\frac{|a-b|}{2}, \min{(a, b)}})=\gcd{(\frac{|3-3|}{2}, \min{(3, 3)}})=\gcd{(0, 3)}\)
現時点で\(a = 3\)、\(b = 3\)ですが、新たに\(a = 0\)、\(b = 3\)とします。

\(a = 0\)と\(b = 3\)では、・・・としたいところですが、\(a=0\)となりましたね。
①より\(\gcd{(0, 3)}=3\)です。
また、★で保存しておいた共通因数の\(2\)を今の\(3\)に掛け合わせます。
\(2×3\)より、\(6\)が元の\(18\)と\(12\)の最大公約数です。
計算の流れはご理解いただけたと思います。
ですが、やはり理屈がわからないと落ち着かないですよね。
ということで、次はバイナリ・ユークリッドの互除法の数学的な解説をします。
証明
\(a\)と\(b\)は自然数として、次の\(4\)つを証明・解説します。
\((1)\) \(\gcd{(a, 0)} = a\)
\((2)\) \(a\)も\(b\)も偶数\(\Rightarrow\)\(\gcd{(a, b)} = 2\gcd{(\frac{a}{2}, \frac{b}{2})}\)
\((3)\) \(a\)のみが偶数\(\Rightarrow\)\(\gcd{(a, b)} = \gcd{(\frac{a}{2}, b)}\)
\((4)\) \(a\)も\(b\)も奇数\(\Rightarrow\)\(\gcd{(a, b)} = \gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\)
\(\gcd{(a, 0)} = a\)の説明をします。
まずは、\(0\)の約数について考えましょう。
そもそもある整数\(n\)の約数とは、\(n\)を割り切れる整数のことでした。
例えば、\(6\)は\(36\)を割り切れるので、\(36\)の約数です。
では、\(6\)は\(0\)を割り切れるでしょうか?
\(0÷6=0\)であり、余りはないので割り切れています。
したがって、\(6\)は\(0\)の約数です。

あれ、これ別に\(6\)に限った話じゃなくない?

良い着眼点ですね。
\(0÷11=0\)や\(0÷100=0\)から\(11\)も\(100\)も\(0\)の約数だとわかります。
つまり、すべての整数は\(0\)の約数なので、当然整数\(a\)も\(0\)の約数です。
また、\(a\)は\(a\)自身を最大公約数として持つので、\(\gcd{(a, 0)} = a\)が導かれます。
実は、この論理では\(\gcd{(0, 0)}\)を上手く説明できません。
しかし、その議論をこの場で行うことは、本筋から逸れるため割愛します。
ご興味のある方は、下記記事が大変参考になるので良かったらどうぞ。
https://qiita.com/reika727/items/9c317bf562b5df966cbf
\(a\)も\(b\)も偶数\(\Rightarrow\)\(\gcd{(a, b)} = 2\gcd{(\frac{a}{2}, \frac{b}{2})}\)の説明をします。
以下、\(a\)と\(b\)は共に偶数より、\(\frac{a}{2}\)と\(\frac{b}{2}\)は整数であることに注意してください。
\(g = \gcd{(\frac{a}{2}, \frac{b}{2})}\)とすると、\(\frac{a}{2} = ga’\)かつ\(\frac{b}{2} = gb’\)です。
ただし、\(a’\)と\(b’\)は互いに素な自然数です。
よって、\(a = 2・\frac{a}{2} = 2ga’\)
同様に、\(b = 2・\frac{b}{2} = 2gb’\)
\(a’\)と\(b’\)は整数より、\(a\)と\(b\)は公約数\(2g\)を持ちます。
さらに、\(a’\)と\(b’\)は互いに素なので、\(a\)と\(b\)の公約数の中では\(2g\)が最大(最大公約数)です。
というのも、\(a’\)と\(b’\)からは、\(1\)以外の正の公約数を出せないからです。
したがって、\(\gcd{(a, b)} = 2g = 2\gcd{(\frac{a}{2}, \frac{b}{2})}\)
\(a\)のみが偶数\(\Rightarrow\)\(\gcd{(a, b)} = \gcd{(\frac{a}{2}, b)}\)の説明をします。
証明しても良いですが、具体例でサクッといきましょう。
例えば、\(54\)と\(45\)の最大公約数を求めましょう。
このとき、\(54\)と\(45\)は\(2\)を公約数に持つ可能性があると思いますか?
いいえ、奇数の\(45\)は\(2\)で割り切れるわけがありません。
\(54 = 2・27\)なので、結局\(27\)の約数と\(45\)の約数を調べていけば十分ですよね。
よって、\(27\)と\(45\)の最大公約数が、元の\(54\)と\(45\)の最大公約数になるのです。
つまり、\(a\)のみが偶数のとき\(\gcd{(a, b)} = \gcd{(\frac{a}{2}, b)}\)です。
\(a\)も\(b\)も奇数\(\Rightarrow\)\(\gcd{(a, b)} = \gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\)の説明をします。
まずは、自然数\(a\)と\(b\)を\(a \ge b\)として\(\gcd{(a, b)} = \gcd{(a – b, a)}\)を証明します。
証明自体はユークリッドの互除法と同様の流れです。
ですが、せっかくなので背理法を使った手法でいきます。
\(g = \gcd{(a, b)}\)とすると、\(a = ga’\)、\(b = gb’\)とおけます。
ただし、\(a’\)と\(b’\)は互いに素な自然数です。・・・①
\(a – b = ga’ – gb’ = g(a’ – b’)\)となり、\(a – b\)も\(g\)を約数に持ちます。
ここで、\(a’\)と\(a’ – b’\)がある素数\(p\)を公約数に持つと仮定しましょう。・・・②
\(a”\)と\(d\)を整数として、\(a’ = pa”\)かつ\(a’ – b’ = pd\)とおけます。
\(a’ – b’ = pd \iff b’ = a’ – pd\)ですから、\(b’ = pa” – pd = p(a” – d)\)です。
\(a” – d\)は整数なので、\(b’\)は\(p\)を約数に持ちます。
②より\(a’\)も\(p\)を約数に持つので、\(p\)はまさに\(a’\)と\(b’\)の公約数です。
しかし、①より\(a’\)と\(b’\)は互いに素でしたので矛盾が生じました。
ゆえに、\(a’\)と\(a’ – b’\)が素数を一切公約数に持たないということは、\(2\)数は互いに素です。
\(a = ga’\)かつ\(a – b = g(a’ – b’)\)かつ\(gcd{(a’ – b’, a)} = 1\)より、\(\gcd{(a – b, a)} = g\)です。
よって、\(\gcd{(a, b)} = \gcd{(a – b, a)}\)が示されました。

え なんで\(\gcd{(a – b, a)}\)だけ?\(\gcd{(a – b, b)}\)じゃダメ?
当然、\(\gcd{(a, b)} = \gcd{(a – b, b)}\)も成り立ちます。
したがって、\(a\)と\(b\)のどちらか小さい方を選べば、計算が効率的ですね。
そこで、\(a\)と\(b\)の小さい方を\(\min{(a, b)}\)として\(\gcd{(a, b)} = \gcd{(a – b, \min{(a, b)})}\)とします。
また、先ほどの証明では\(a – b\)が負の数にならないように\(a \ge b\)としました。
しかし、\(b \ge a\)ならば\(b – a\)とするだけです。
大小関係を考慮せずに済むために、絶対値を使います。
その結果、\(\gcd{(a, b)} = \gcd{(|a – b|, \min{(a, b)})}\)となるのです。
最後に、そもそも\(a\)と\(b\)は奇数を想定しているので\(a – b\)は必ず偶数になります。
つまり、\(a – b\)は偶数で\(\min{(a, b)}\)は奇数です。
先ほど、\(a\)が偶数かつ\(b\)が奇数ならば\(\gcd{(a, b)} = \gcd{(\frac{a}{2}, b)}\)を確認しました。
よって、\(\gcd{(a, b)} = \gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\)となるのです。
プログラム
バイナリ・ユークリッドの互除法の考案には、処理が遅い剰余演算子%の使用を回避するという背景もありました。
(私の環境ではまったく遅いとは感じませんが・・・。)
したがって、アルゴリズム内で数多く行う\(2\)の乗除算には、*や%を使わずにビット演算子を駆使します。
binary_gcd関数は、バイナリ・ユークリッドの互除法で\(2\)数の最大公約数を求めます。
def binary_gcd(a, b):
if a == 0:
return b
if b == 0:
return a
a, b = abs(a), abs(b)
if (a | b) & 1 == 0: # aとbが偶数の場合
return binary_gcd(a >> 1, b >> 1) << 1
if a & 1 == 0: # aが偶数の場合
return binary_gcd(a >> 1, b)
if b & 1 == 0: # bが偶数の場合
return binary_gcd(a, b >> 1)
return binary_gcd(abs(a - b) >> 1, min(a, b)) # aとbが奇数の場合実行例です。
num1 = 527
num2 = 341
result = binary_gcd(num1, num2)
print(result)
# 31恐らく多くの方がこの条件式を疑問に思ったのではないでしょうか。
if (a | b) & 1 == 0: # aとbが偶数の場合実質的に下の記述と同じですが、なぜ判定が可能なのかを解説します。
if a % 2 == 0 and b % 2 == 0: # aとbが偶数の場合まずはビット演算子を軽く復習しましょう。
| 名前 | 記号 | 説明 |
|---|---|---|
| ビット単位論理積 | & | 2つのビット列の各ビットをAND演算して新しいビット列を作る。 |
| ビット単位論理和 | | | 2つのビット列の各ビットをOR演算して新しいビット列を作る。 |
| 左ビットシフト | << | ビット列の各ビットを指定された数だけ左にシフトする。 |
| 右ビットシフト | >> | ビット列の各ビットを指定された数だけ右にシフトする。 |
binary_gcd関数で使うビット演算子以上を踏まえ、まずは偶数を\(2\)進数にすると最下位ビットが必ず\(0\)になる事実に着目します。
0010 # 10進数で2
0100 # 10進数で4
0110 # 10進数で6
1000 # 10進数で8
1010 # 10進数で10仮にどちらも偶数の場合、ビット単位論理和で最下位ビットは必ず\(0\)です。
ビット単位論理和 (4 | 10)
0100 # 10進数で4
1010 # 10進数で10
---
1110 # 10進数で14そして、今度は先ほどの\(1110\)と\(1\)でビット単位論理積を取ると、結果は必ず\(0\)です。
ビット単位論理積 (14 & 1)
1110 # 10進数で14
0001 # 10進数で1
---
0000 # 10進数で0つまり、どちらも偶数の場合は、一連の計算の結果は\(0\)になります。
再度コードに戻りましょう。
まずは、\(a\)と\(b\)のビット単位論理和を取り、その結果と\(1\)とのビット単位論理積を取ります。
(a | b) & 1この結果が\(0\)であれば偶数なので、判定は次のようになるのです。
if (a | b) & 1 == 0: # aとbが偶数の場合上記が理解できれば、その後の条件式も同じ理屈です。
if a & 1 == 0: # aが偶数の場合
・・・
if b & 1 == 0: # bが偶数の場合
・・・また、左ビットシフト<<は\(10\)進数だと\(2\)倍する計算です。
反対に、右ビットシフト>>は\(10\)進数で\(\frac{1}{2}\)倍する計算です。
return binary_gcd(a >> 1, b >> 1) << 1左ビットシフトと右ビットシフトが、それぞれなぜ\(2\)倍・\(\frac{1}{2}\)倍なのかは後日記事にします。
記事になるのを待つよりもググった方が早いかもしれません。
いかがでしょうか。
再度アルゴリズムとコードを確認すると、より理解が深まると思います。
\(2\)数の最大公約数を求めるプログラムの応用
これまで作った\(2\)数の最大公約数を求めるプログラムを応用しましょう。
本記事では、次の事例を紹介します。
\(3\)つ以上の最大公約数を求める
\(3\)つ以上の自然数の最大公約数を求める
\(3\)つ以上の自然数であっても、考え方は先ほどと同様です。
例えば、\(18\)と\(24\)と\(33\)で考えましょう。
一気に\(3\)つ考えると大変なので、まずは\(18\)と\(24\)の最大公約数(\(\gcd{(18, 24)}\))から求めます。
そして最後に\(\gcd{(18, 24)}\)と\(33\)の最大公約数を求めるという流れです。
\(18\)と\(24\)の最大公約数は\(6\)ですね。
次に、\(6\)と\(33\)の最大公約数を考えますが、\(6\)では\(33\)を割り切れません。
しかし、\(6\)の約数である\(3\)だと\(33\)を割り切れます。
ということは、\(3\)ならば\(18\)と\(24\)と\(33\)をすべて割り切れます。
これ以上に大きな公約数は存在しないため、\(3\)が最大公約数です。
今の話を一般化しましょう。
\(3\)つの自然数\(a_1\), (a_2\), \(a_3\)の最大公約数を求める過程は、次のようになります。

\(4)つの自然数\(a_1\), (a_2\), \(a_3\), \(a_4\)の場合です。
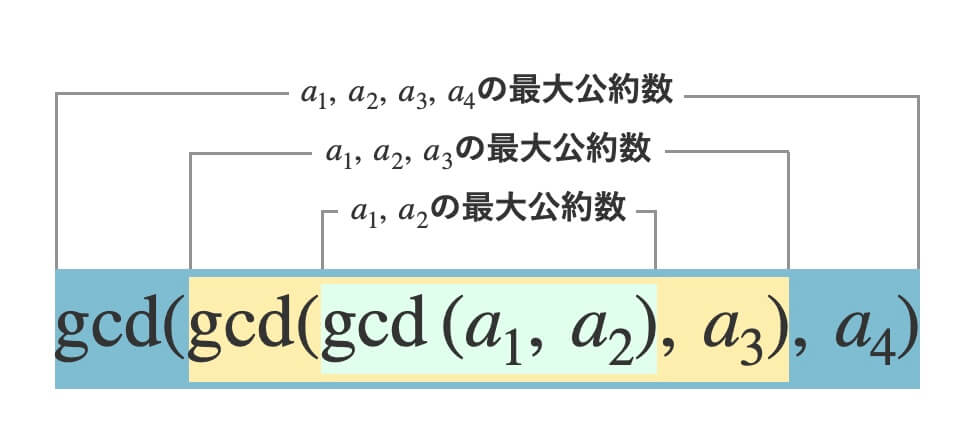
そして\(n\)数間の場合です。
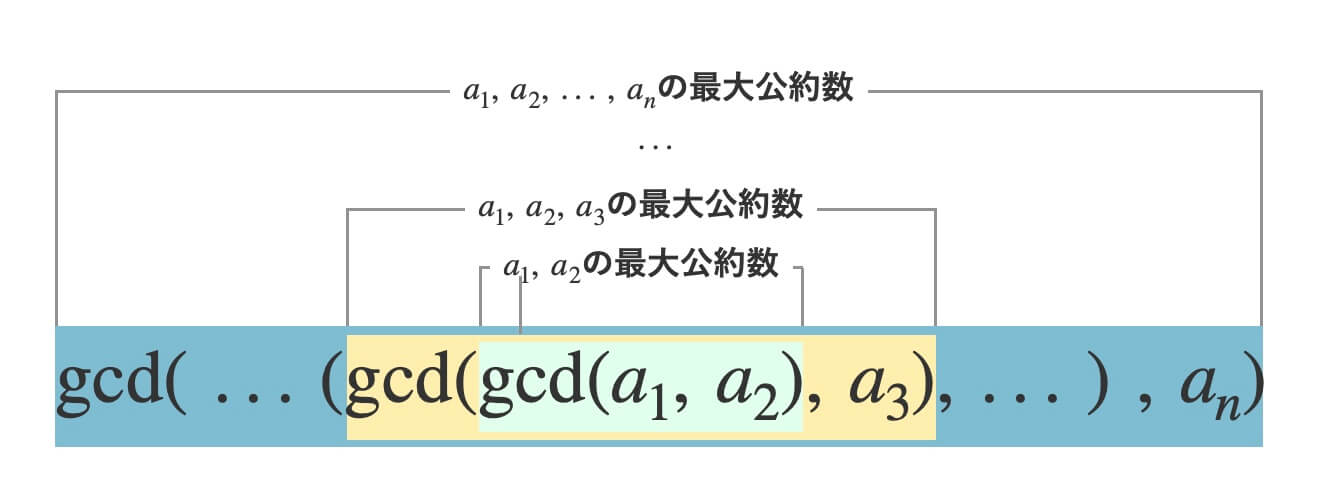
これをプログラムに落とし込んでいきます。
以下は、\(3\)つ以上の自然数の最大公約数を求めるgcd関数です。
def gcd(*numbers):
# 引数が渡されていない場合に0を返す
if not numbers:
return 0
# 最初の数を gcd_result に代入
gcd_result = numbers[0]
# 2番目以降の数について順に最大公約数を計算
for num in numbers[1:]:
gcd_result = euclidean_gcd(gcd_result, num)
# 最終的な最大公約数を返す
return gcd_result
for文内でeuclidean_gcd関数を使っています。
代わりにbinary_gcd関数でも構いません。
実行例です。
print(gcd_multiple(24, 36, 48)) # 結果: 12
print(gcd_multiple(54, 24, 81)) # 結果: 3まとめ
今回は、最大公約数を求めるアルゴリズムを\(2)つご紹介しました。
\(1\)つ目は、ユークリッドの互除法です。
自然数\(a\)と\(b\)\((a\ge b)\)の最大公約数を求める。
- \(b=0\)ならば、\(a\)を最大公約数としてアルゴリズムを終了する。
- \(a\)を\(b\)で割った余り\(r\)を求める。
- \(a=b\)、\(b=r\)として①に戻る。
\(2\)つ目は、バイナリ・ユークリッドの互除法です。
自然数\(a\)と\(b\)の最大公約数を求める。
- \(a=0\)ならば、\(\gcd{(a,b)}=b\)とする。\(a\)と\(b\)が逆でも同様。
- \(a\)も\(b\)も偶数ならば、\(\gcd{(a,b)}=2 \gcd{(\frac{a}{2}, \frac{b}{2})}\)とする。
- \(a\)のみが偶数ならば、\(\gcd{(a,b)}=\gcd{(\frac{a}{2},b)}\)とする。\(a\)と\(b\)が逆でも同様。
- \(a\)も\(b\)も奇数ならば、\(\gcd{(a,b)}=\gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\)とする。
| \(a\) | \(b\) | \(\gcd{(a, b)}\) | 備考 |
|---|---|---|---|
| \(a\) | 0 | \(a\) | \(a\)と\(b\)が逆でも同様。 |
| 偶数 | 偶数 | \(2 \gcd{(\frac{a}{2}, \frac{b}{2})}\) | |
| 偶数 | 奇数 | \(\gcd{(\frac{a}{2},b)}\) | \(a\)と\(b\)が逆でも同様。 |
| 奇数 | 奇数 | \(\gcd{(\frac{|a-b|}{2}, \min{(a, b)})}\) |
なお、本記事では関数を作りましたが、
実は最大公約数を求める関数はPythonの標準ライブラリに既にあります。
ですが、プログラミング上達の鍵は実際にコードを書くことにあります。
実際にご自身の手で書くことで、アルゴリズムへの理解もグッと深まるはずです。
最後までご覧いただき、ありがとうございました。