任意点周りの回転移動を２通り解説！プログラムで自動化！

この記事で解決できるお悩み

こんなお悩みを解決します。

この記事の内容

こんにちは、Youta(@youta_blog)です。

今回は「座標平面上での点の回転」「回転後の座標を出すプログラム」についてのお話です。

あなたは学生時代、以下のような問題を見たことはありますか？

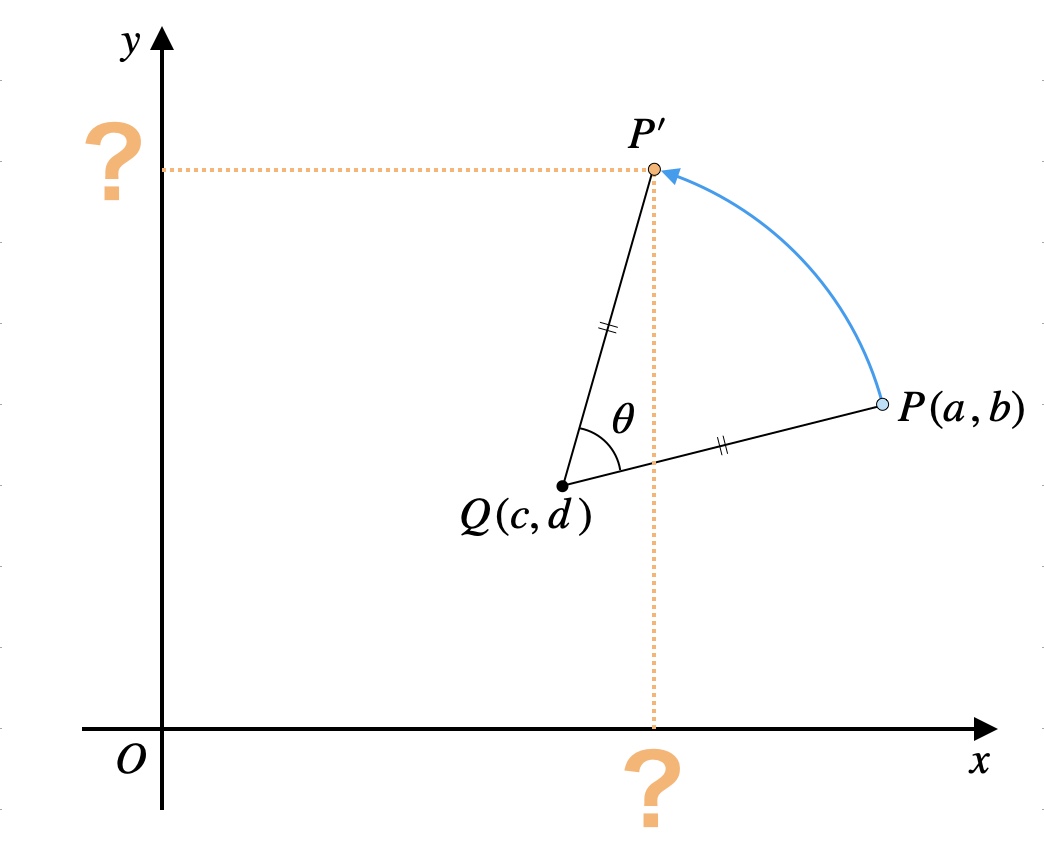
$xy$平面上に点$P(a, b)$と点$Q(c, d)$がある。

点$Q$を中心に、点$P$を反時計回りに$\theta$回転させた点を$P’$とする。

ただし、$PQ=P’Q$である。

このとき、点$P’$の座標を求めよ。

[20 慶應義塾大 薬学 7 改題]

解法を忘れてしまったり、そもそもどう解けばいいかわからない…という方が多いのではないでしょうか。

でもご安心ください！

本記事では、こうした問題に対処できる２通りのアプローチを解説します。

合わせて、コンピュータに自動で解かせるためのプログラムもご紹介します。

回転後の座標を導出する方法

まず始めに冒頭の問題の答えを示します。

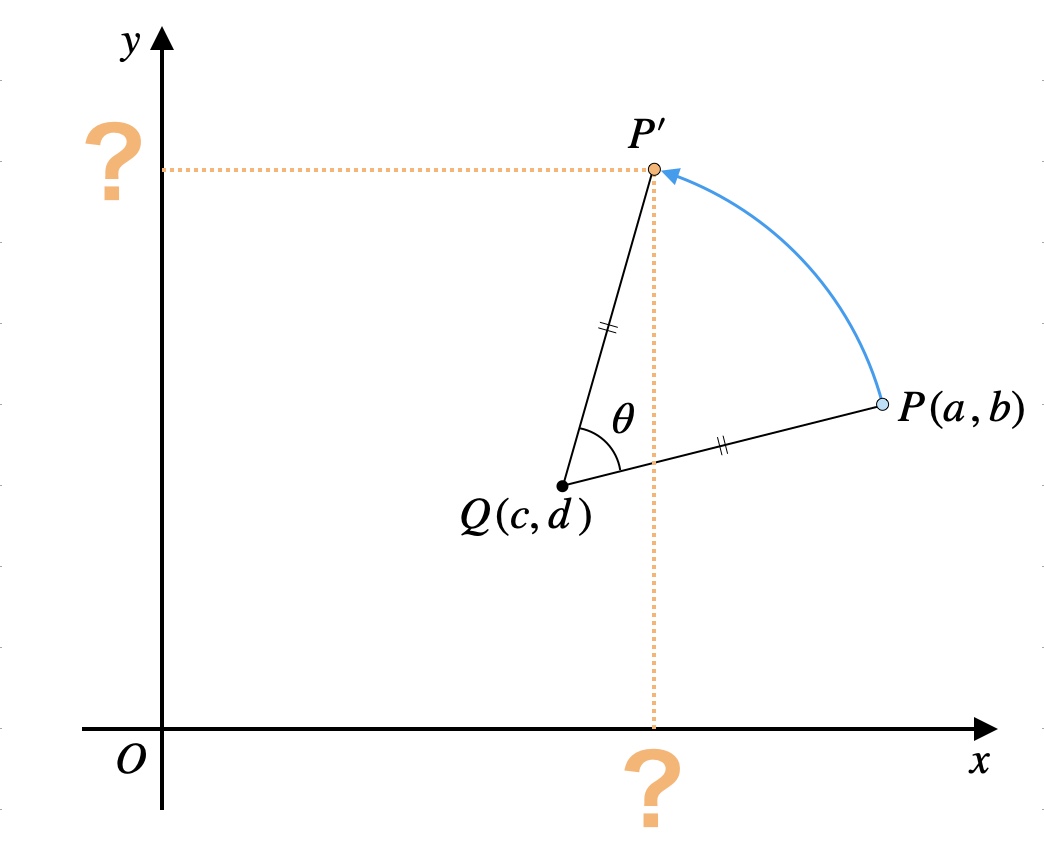
答え

三角関数を使うやり方

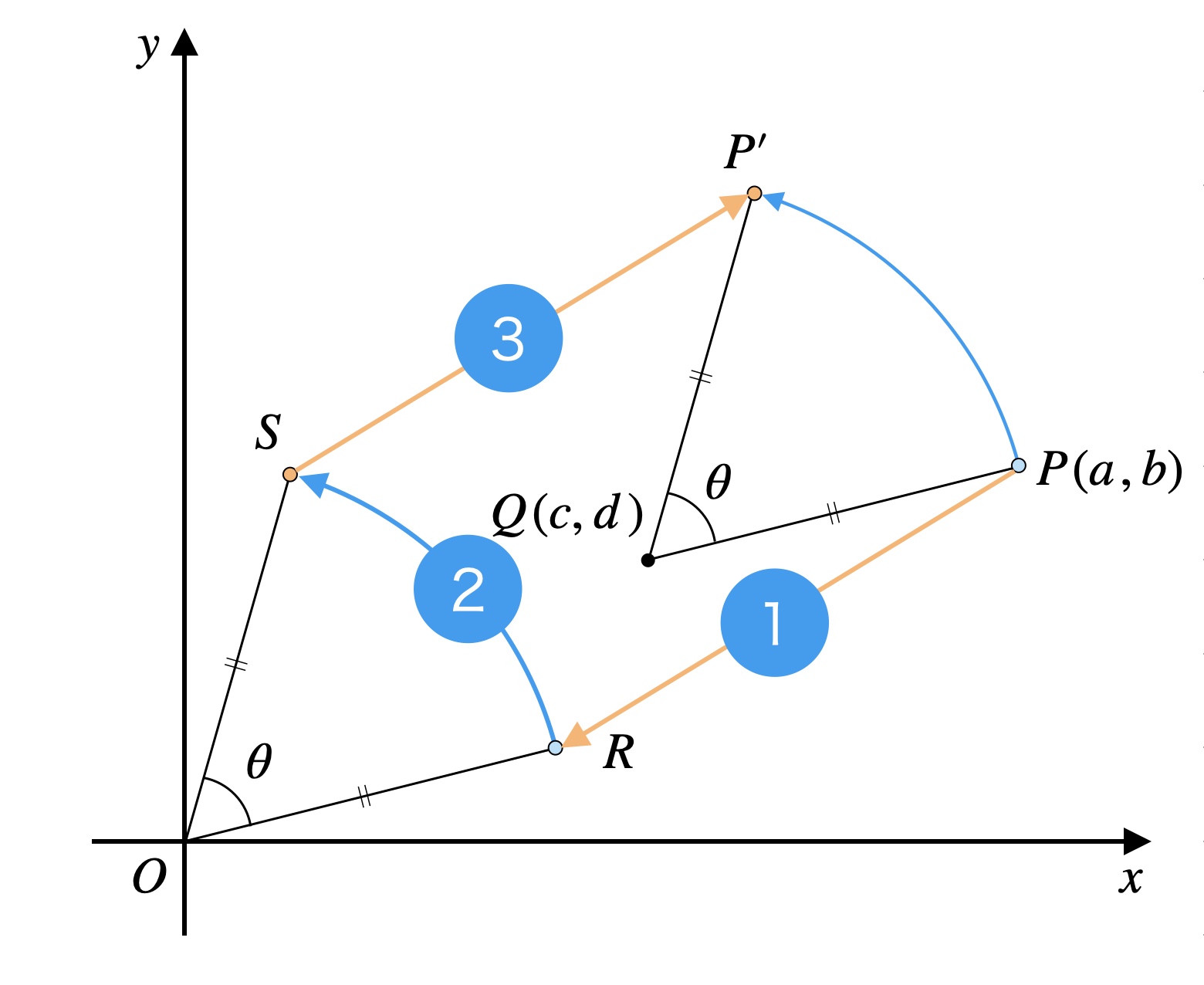
手順は簡単。たった3ステップです。

1ステップずつ詳しく見ていきましょう。

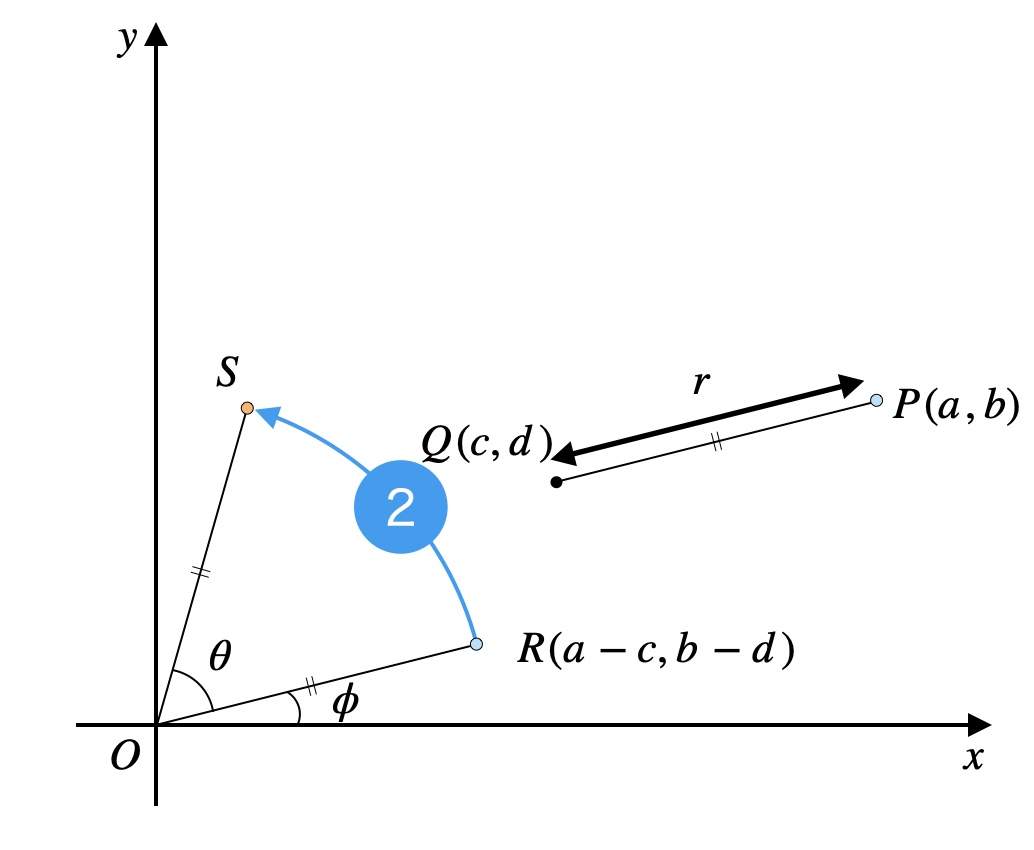
平行移動→$R$の座標計算

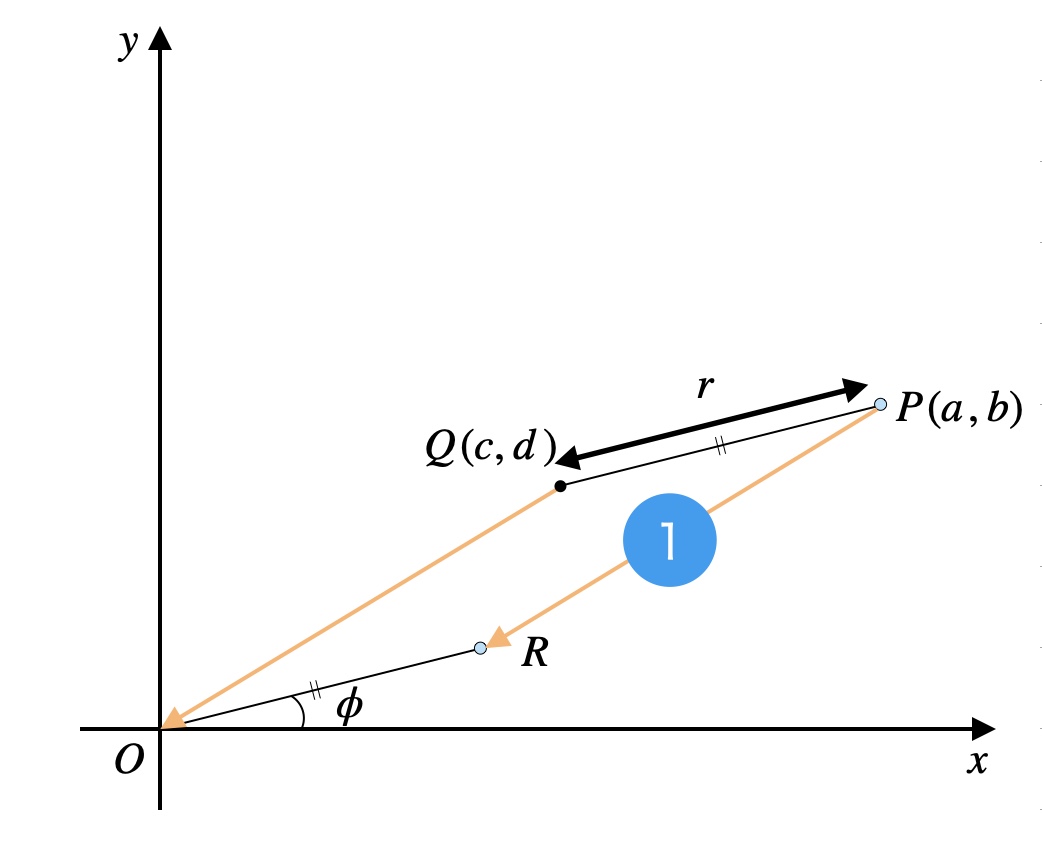
まずは新しい変数を導入します。

最終的に消えてしまう変数ですので怖がらないでくださいね。

線分$PQ$を、$Q$が原点$O$に重なるように平行移動させます。

原点が回転の中心となるようにするためです。

では、これから本題の$P$の移動先$R$の座標を考えましょう。

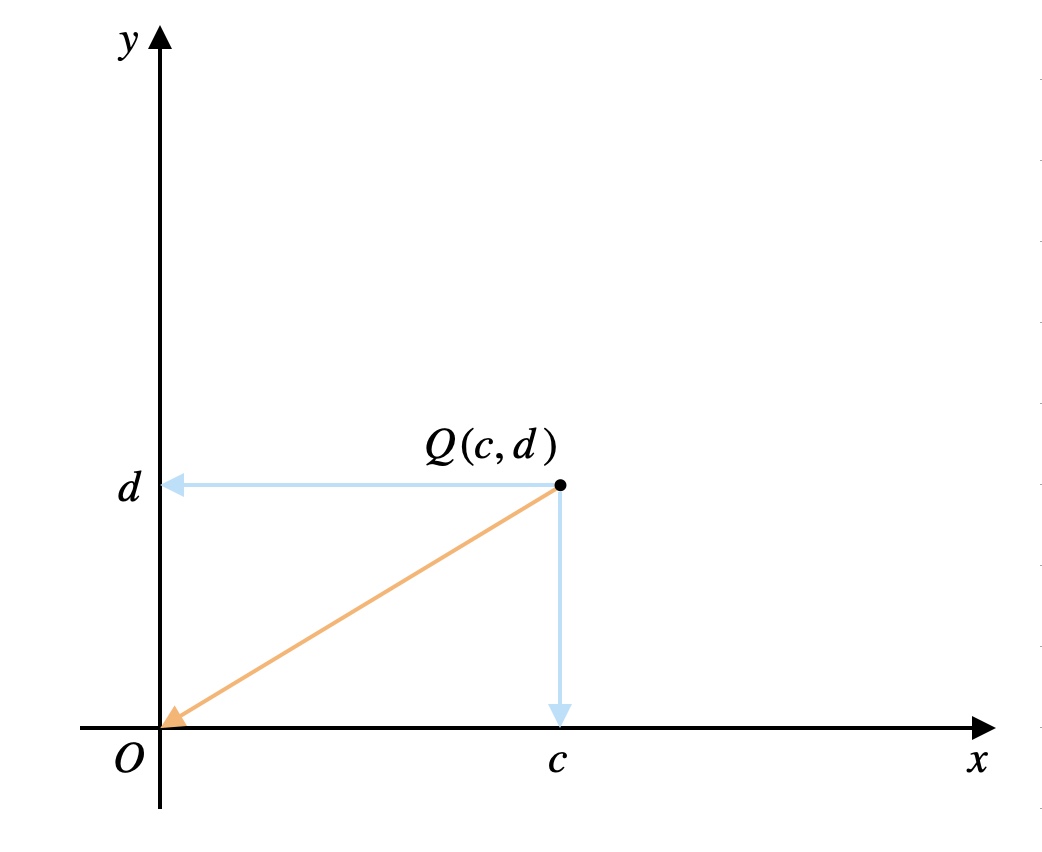
そもそも$Q$から原点$O$に行くためには、$Q$を$x$軸方向に$-c$、$y$軸方向に$-d$だけ平行移動すればよいですね。

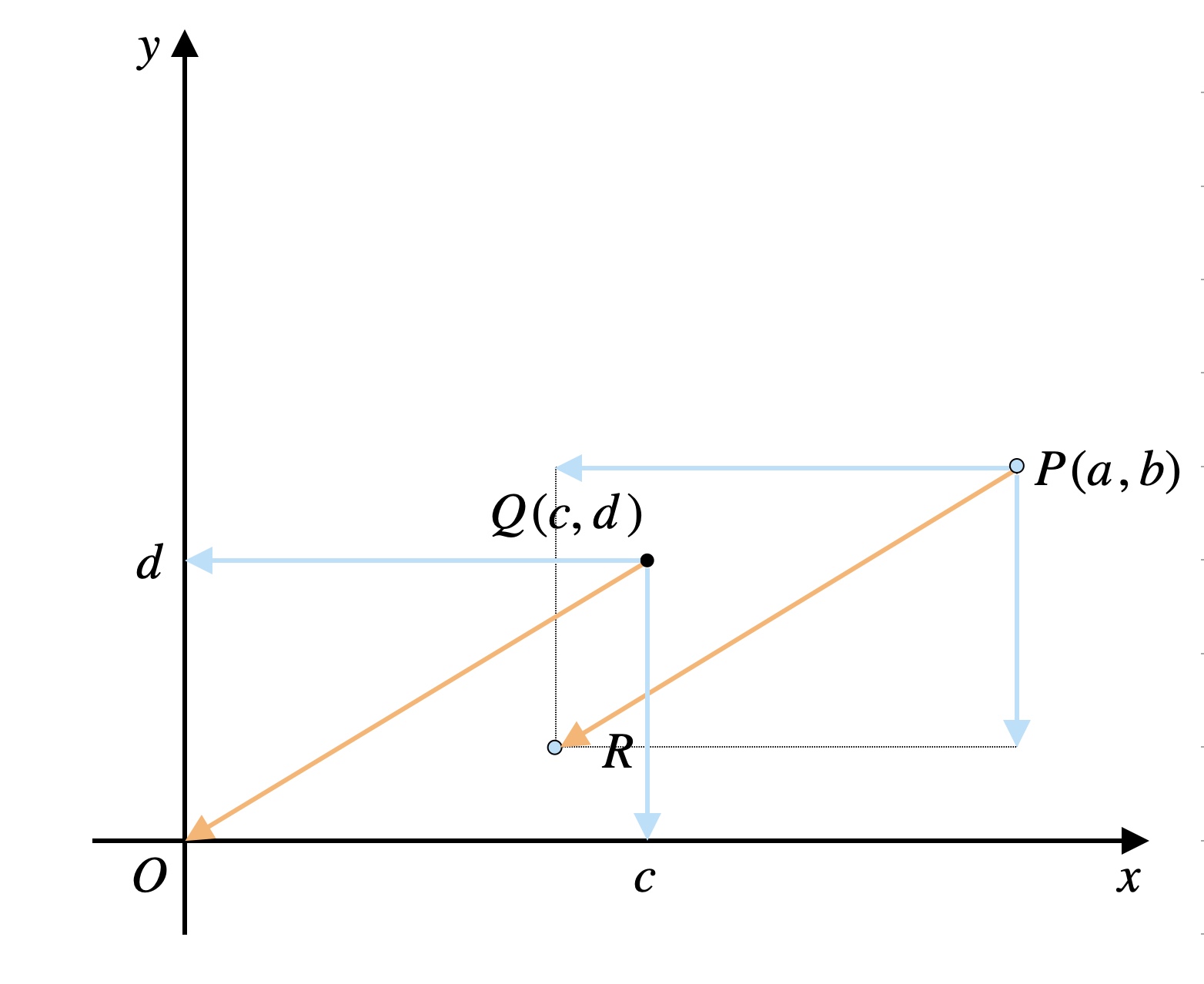
ということは$P$から$R$に行くのも同様、$P$を$x$軸方向に$-c$、$y$軸方向に$-d$だけ平行移動すればよいです。

よって、$R$の座標が求まりました。

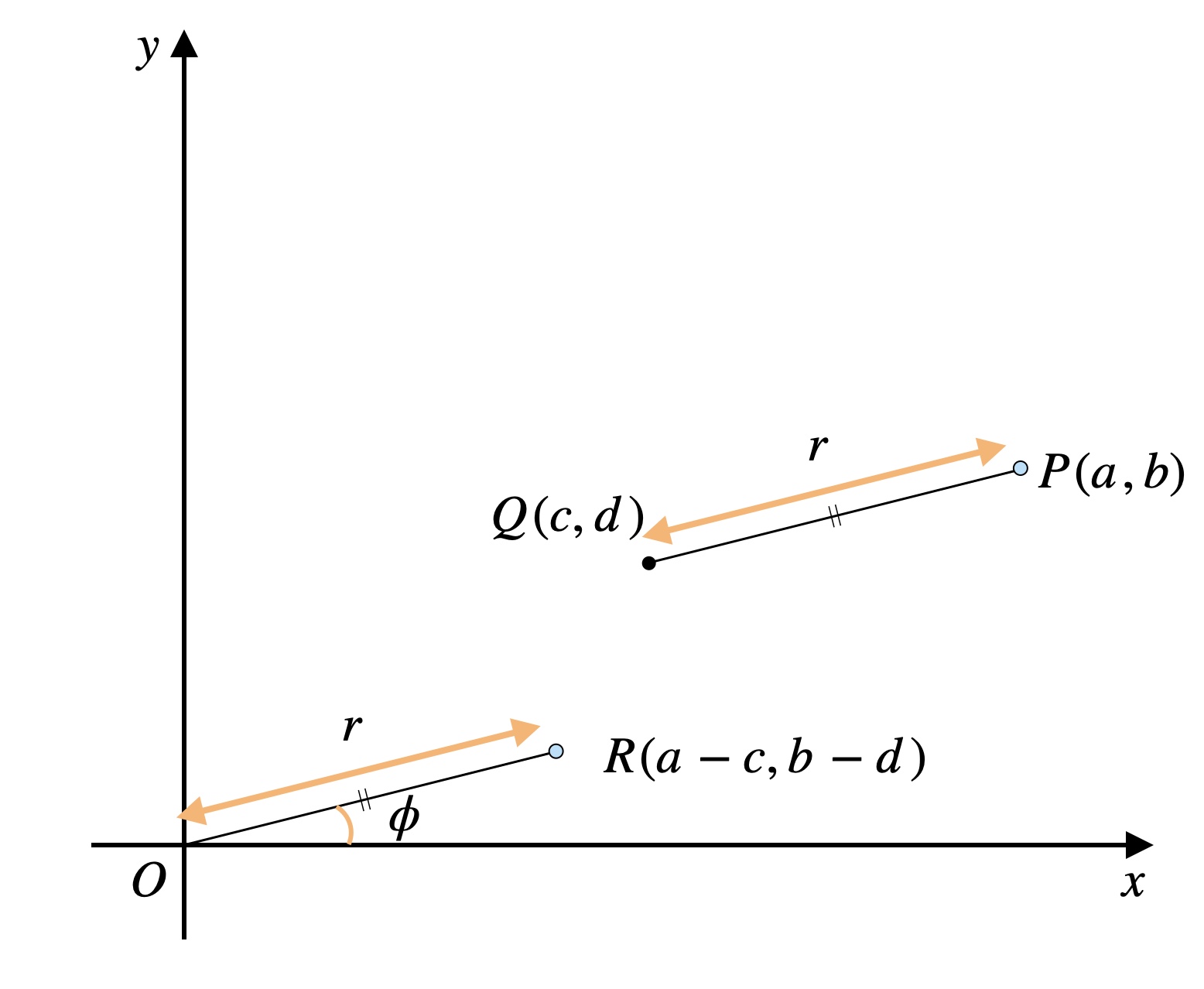
さらに角度$\phi$と動径$OR$に着目すると、三角関数の定義により$R$の座標は別の形でも表せます。

加法定理→$S$の座標計算

次は、$R$を原点を中心に角度$\theta$だけ回転させた点$S$の座標を求めます。

$r=PQ=RO=SO$であるので、先ほどと同様に三角関数の定義により$S$の座標は以下のようになります。

ここで三角関数の加法定理を使います。

上記の公式と先ほどの$R$の座標を考慮すると、$S$の座標が以下のように計算できます。

平行移動→$P’$の座標計算

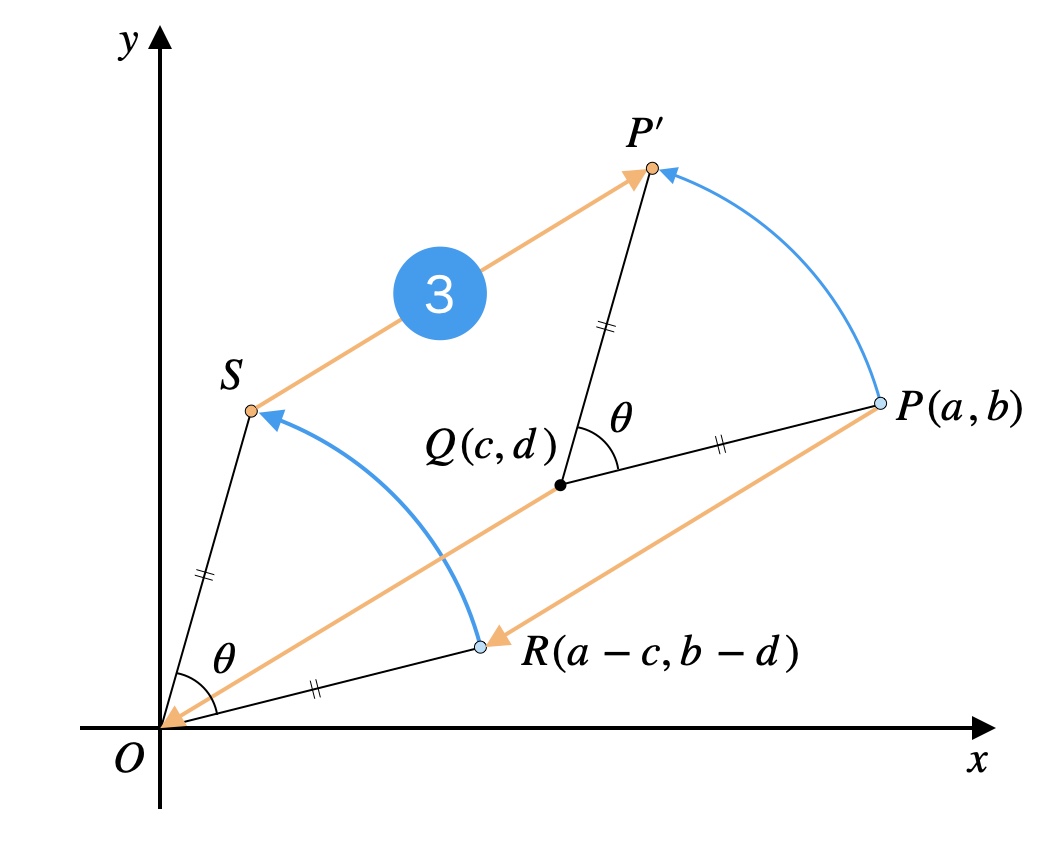
最後に、$S$を平行移動して$P’$を求めましょう。

平行移動量はSTEP1の平行移動→$R$の座標計算のときと真逆です。

つまり、$S$を$x$軸方向に$c$、$y$軸方向に$d$だけ平行移動します。

大変でしたね…。

以上が、三角関数を使っての導出の流れです。

先ほどの答えと一致していればOKです！

複素数平面を使うやり方

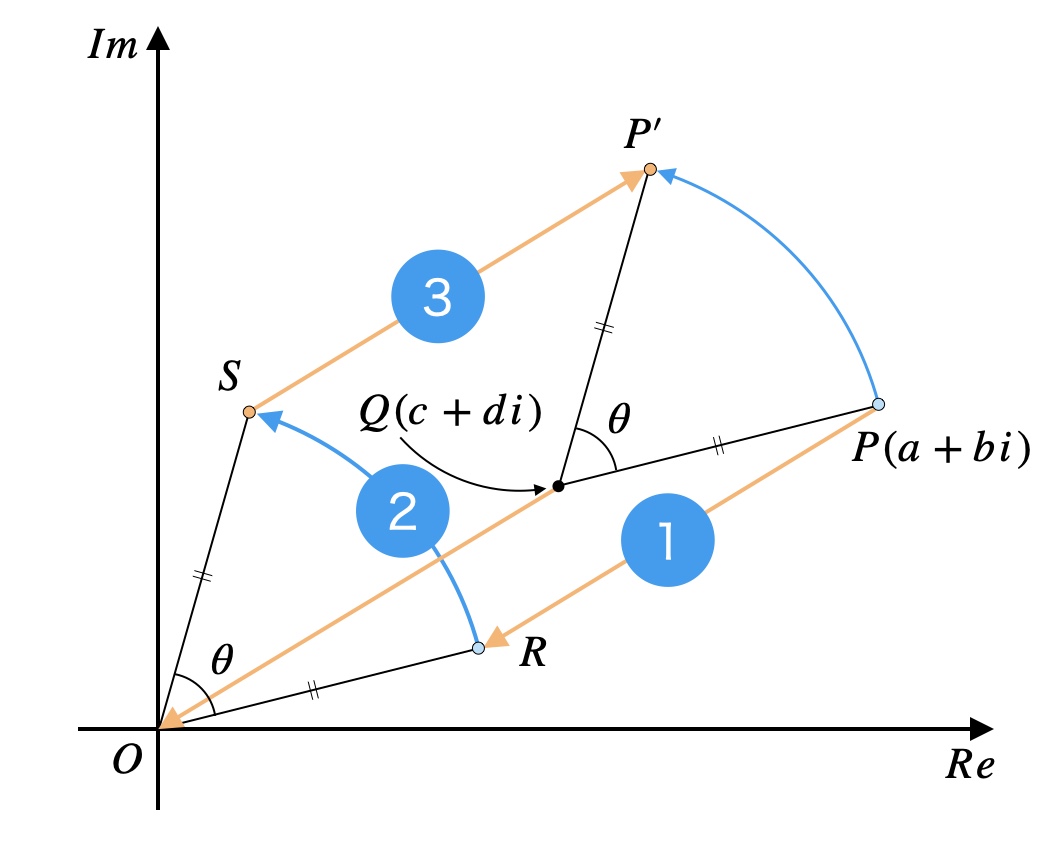
こちらも手順は3ステップからなります。

2以外は三角関数のときとほとんど変わらないのでご安心ください。

1ステップずつ詳しく見ていきます。

平行移動→$R$の座標計算

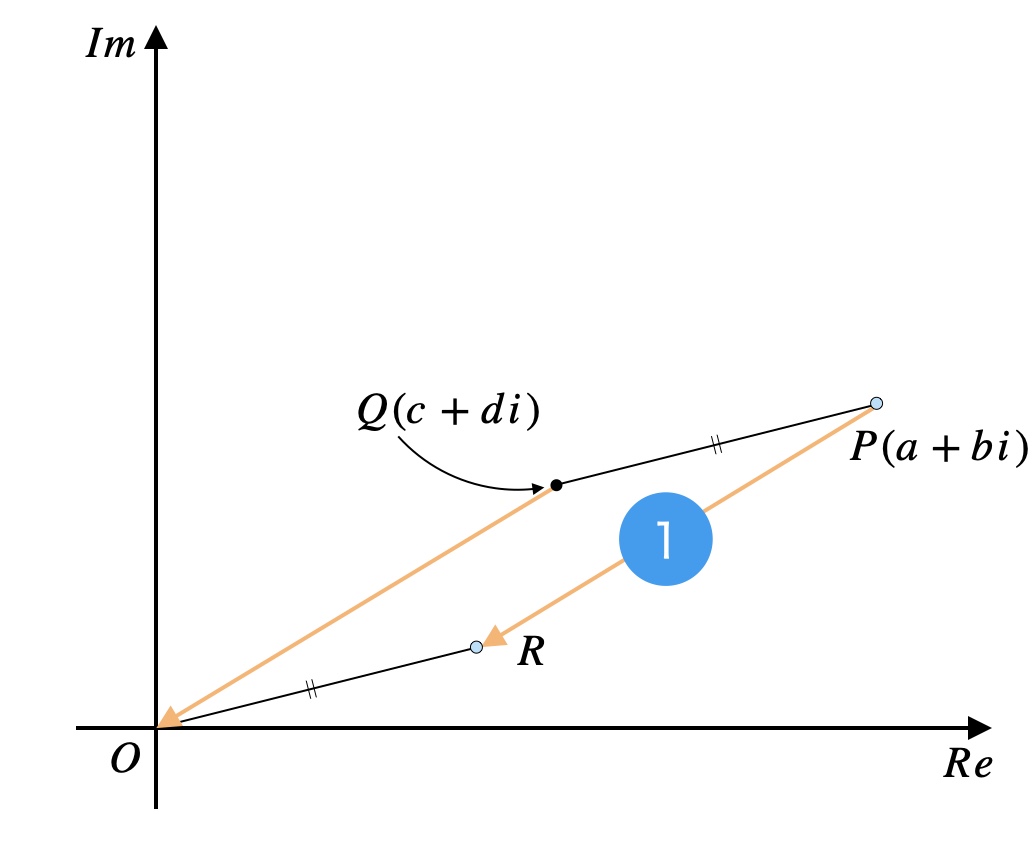
線分$PQ$を、$Q$が原点$O$に重なるように平行移動させます。

原点が回転の中心となるようにするためです。

では、これから本題の$P$の移動先である$R$の座標を考えましょう。

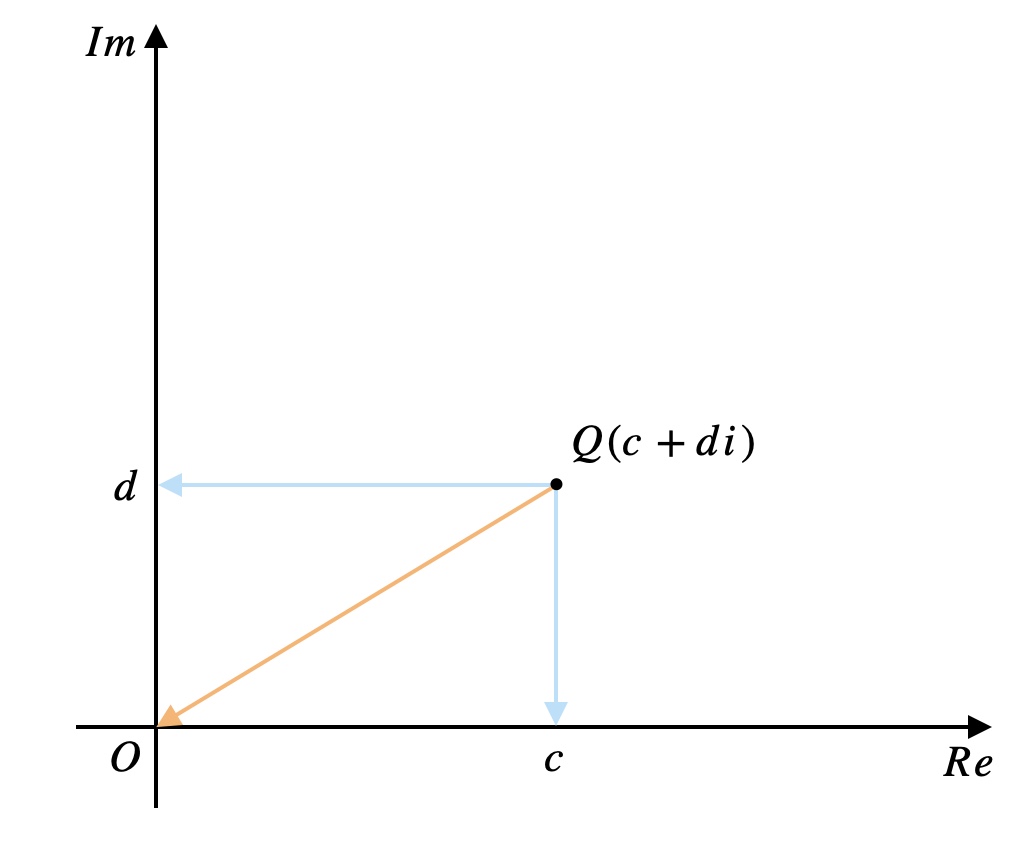
そもそも$Q$から原点$O$に行くためには、$Q$を実軸方向に$-c$、虚軸方向に$-d$だけ平行移動すればよいですね。

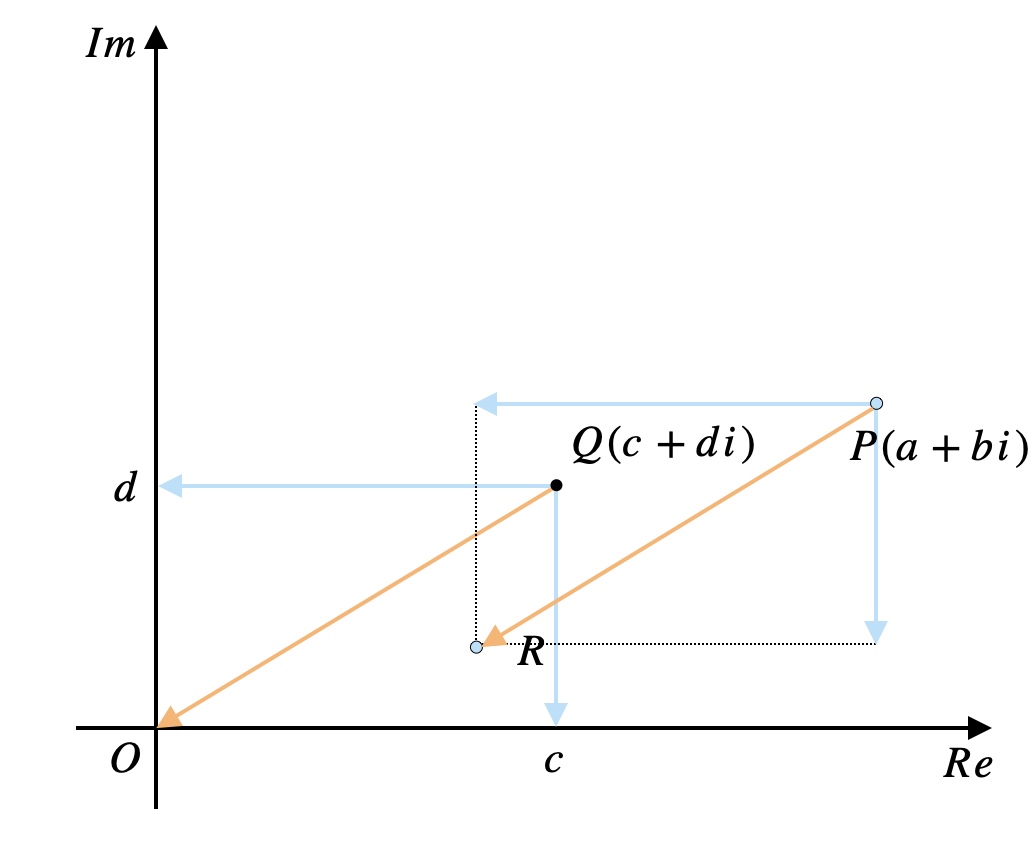
ということは$P$から$R$に行くのも同様、$P$を実軸方向に$-c$、虚軸方向に$-d$だけ平行移動すればよいです。

よって、点$R$が表す複素数が求まりました。

回転移動→$S$の座標計算

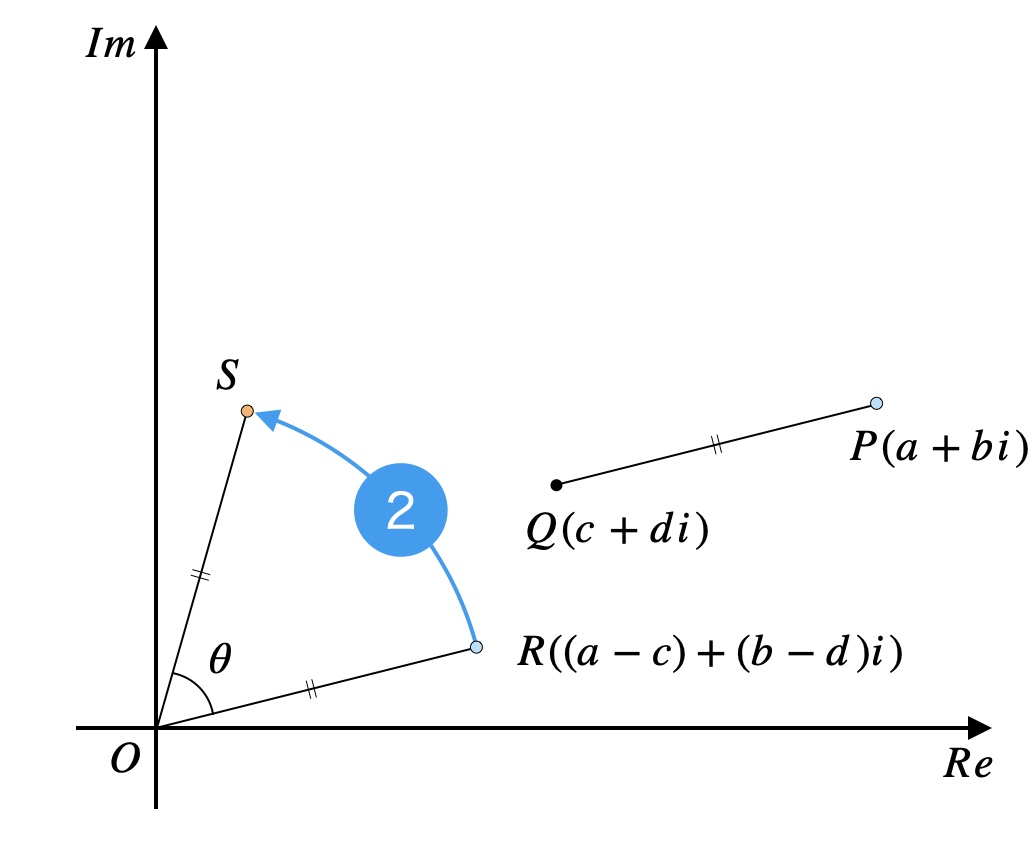
次は、$R$を原点を中心に角度$\theta$だけ回転させた点$S$の座標を求めます。

複素数平面に関して、以下の事実が成り立つことを利用します。

上記の事実と先ほどの$R$が表す複素数を考慮すると、$S$が表す複素数を以下のように計算できます。

平行移動→$P’$の座標計算

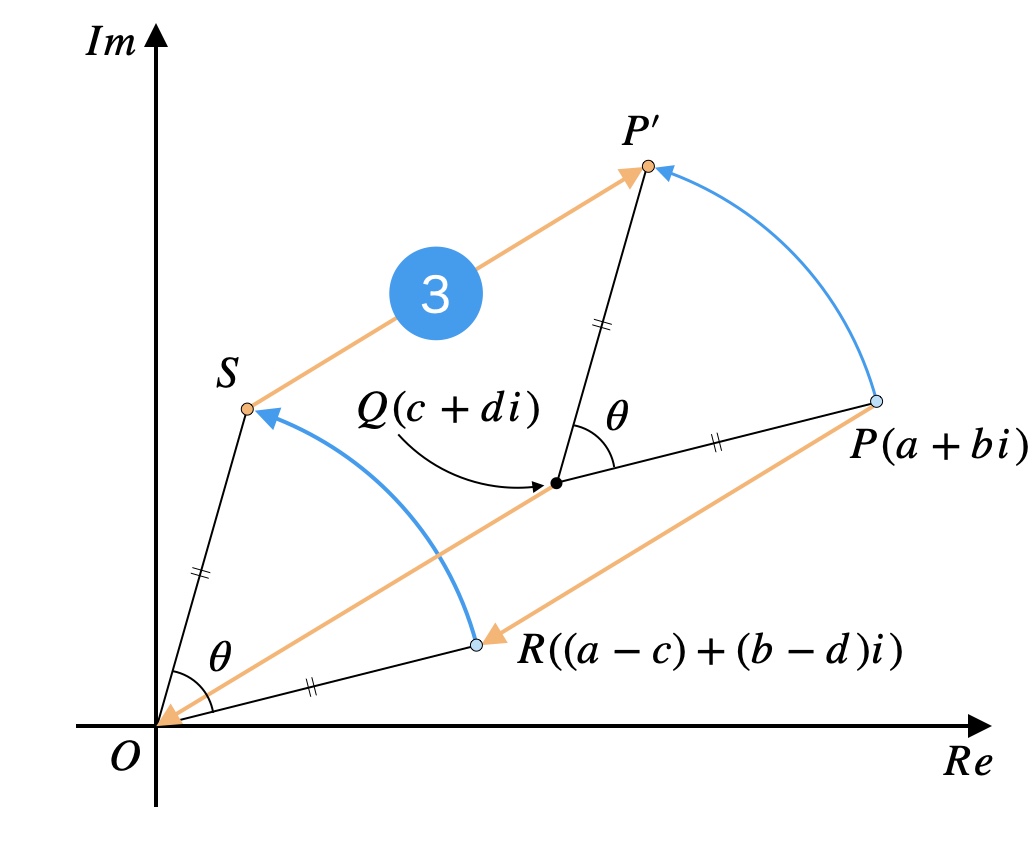
最後に、$S$を平行移動して$P’$を求めましょう。

平行移動量はSTEP1の平行移動→$R$の座標計算のときと真逆です。

つまり、$S$を実軸方向に$c$、虚軸方向に$d$だけ平行移動します。

複素数平面上の実軸と虚軸の値は、それぞれ$xy$平面上での$x$軸・$y$軸の値です。

よって、これで点$xy$平面上での$P’$の座標が求まりました。

以上が、複素数平面を使った導出の流れです。

どちらでも同じ答えが出るのが面白いですね！

任意の点周りで座標を回転させるプログラムの実装

先ほどの理論を踏まえた上で、実際にプログラムを書いてみましょう。

以下に、指定した点を中心に座標を回転させる関数の実装例を示します。

実装例

import math


def rotate_point(point, center, angle, is_radian=False):
    # 点を中心周りに指定された角度分回転させる関数
    # point: 回転させる点の座標。一つ以上の座標を格納したタプル(リスト)。 (x, y) or (x1, y1, x2, y2, ...xn, yn)
    # center: 回転中心の座標 (x, y)
    # angle: 回転角度。デフォルトでは度数法。
    # is_radian: Trueの場合はangleを弧度法、Falseの場合は度数法で指定する。
    # 戻り値: 回転後の座標 (x, y) or (x1, y1, x2, y2, ...xn, yn)

    # 角度が度数法の場合は弧度法に変更
    if not is_radian:
        angle = math.radians(angle)

    sin_angle = math.sin(angle)
    cos_angle = math.cos(angle)

    # 回転した座標を格納するリスト
    rotated_points = []

    for i in range(0, len(point), 2):
        x, y = point[i] - center[0], point[i + 1] - center[1]

        # 回転後の座標を計算
        rotated_x = x * cos_angle - y * sin_angle + center[0]
        rotated_y = y * cos_angle + x * sin_angle + center[1]

        rotated_points.extend((rotated_x, rotated_y))

    return rotated_points
   

上記のコードでは、ある座標を中心周りに指定角度分回転させた座標を返す関数rotate_pointを定義しています。

テスト

単一座標の回転

手始めに、慶應義塾大学の入試問題でも解かせましょう。

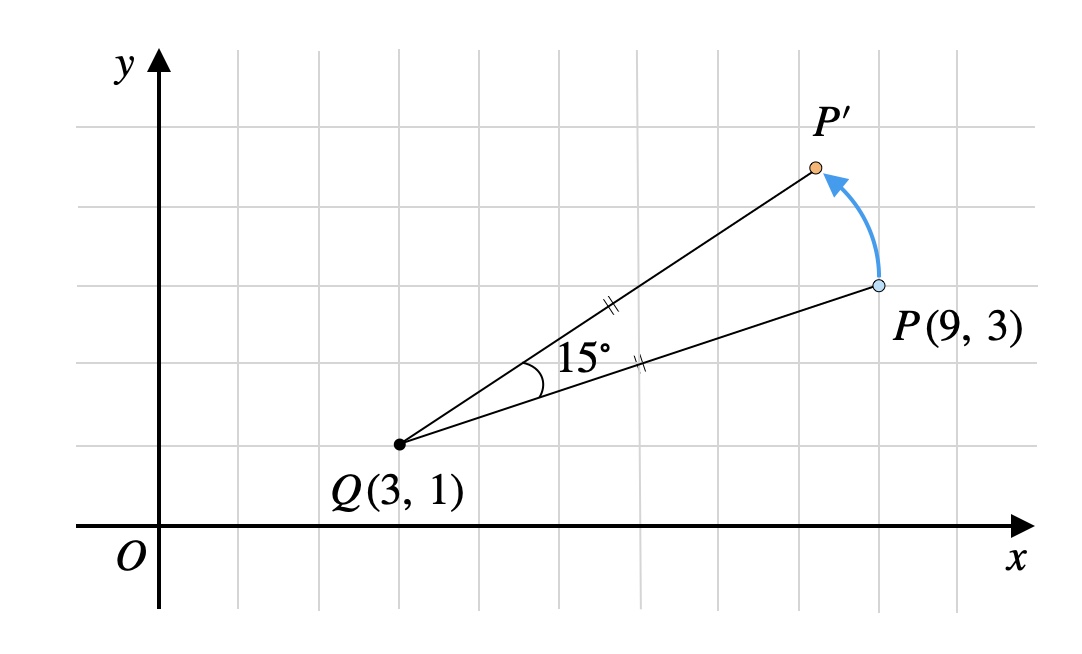
$xy$平面上に点$P(9, 3)$と点$Q(3, 1)$がある。

点$Q$を中心に、点$P$を反時計回りに$15°$回転させた点を$P’$とする。

ただし、$PQ=P’Q$である。

このとき、点$P’$の座標を求めると、$x$座標は□である。

[20 慶應義塾大 薬学 7]

答え

先ほどのコードの下に、以下のテストを書いて実行します。

p = (9, 3)  # 回転させたい座標
q = (3, 1)  # 中心の座標
theta = 15  # 回転角度(度数法)

answer = rotate_point(p, q, theta)

print(answer)  # 結果出力
-->[8.277916867529369, 4.484765923193261]

複数座標の回転

実は先ほどのプログラムは、複数の座標を一気に回転させることができます。

ということで、次は図形の回転問題です。

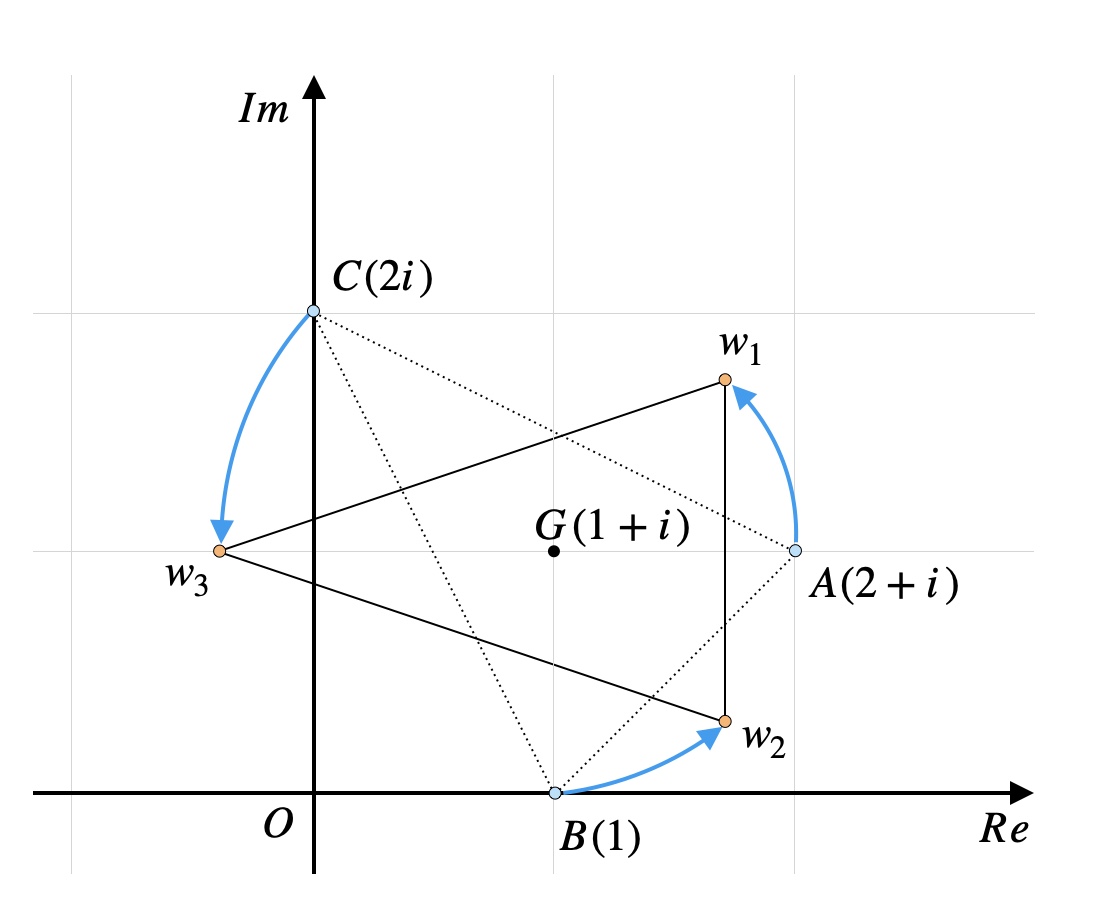
複素数平面上の3点$A,\ B,\ C$を表す複素数をそれぞれ

$$\begin{gather} z_1=2+i,\ z_2=1,\ z_3=2i \\ \end{gather}$$

とするとき、以下の問に答えなさい。

(1) $\triangle{ABC}$の重心$G$を表す複素数$g$を求めなさい。

(2) 点$A,\ B,\ C$をそれぞれ点$G$を中心に$\frac{\pi}{4}$だけ回転した点を表す複素数$w_1,\ w_2,\ w_3$を求めなさい。

 [22 福岡女子大 環境科学 2]

答え

複素数が出てきますので、$xy$平面上の点に置換してテストをします。

先ほどのコードの下に、以下のテストを書いて実行します。

coords = (2, 1, 1, 0, 0, 2)  # 順にA, B, Cの座標 (A_x, A_y, B_x, B_y, C_x, C_y)
g = (1, 1)  # 三角形の重心
theta = math.pi / 4  # 回転角度(ラジアン)

answer = rotate_point(coords, g, theta, True)  # 角度がラジアンなので最後にTrueを入れる。

print(answer)  # 結果出力
-->[1.7071067811865475, 1.7071067811865475, 1.7071067811865475, 0.2928932188134524, -0.4142135623730949, 1.0]

任意の点周りで座標を回転させるプログラムの活用例

最後に、この点の回転が活躍する例をご紹介します。

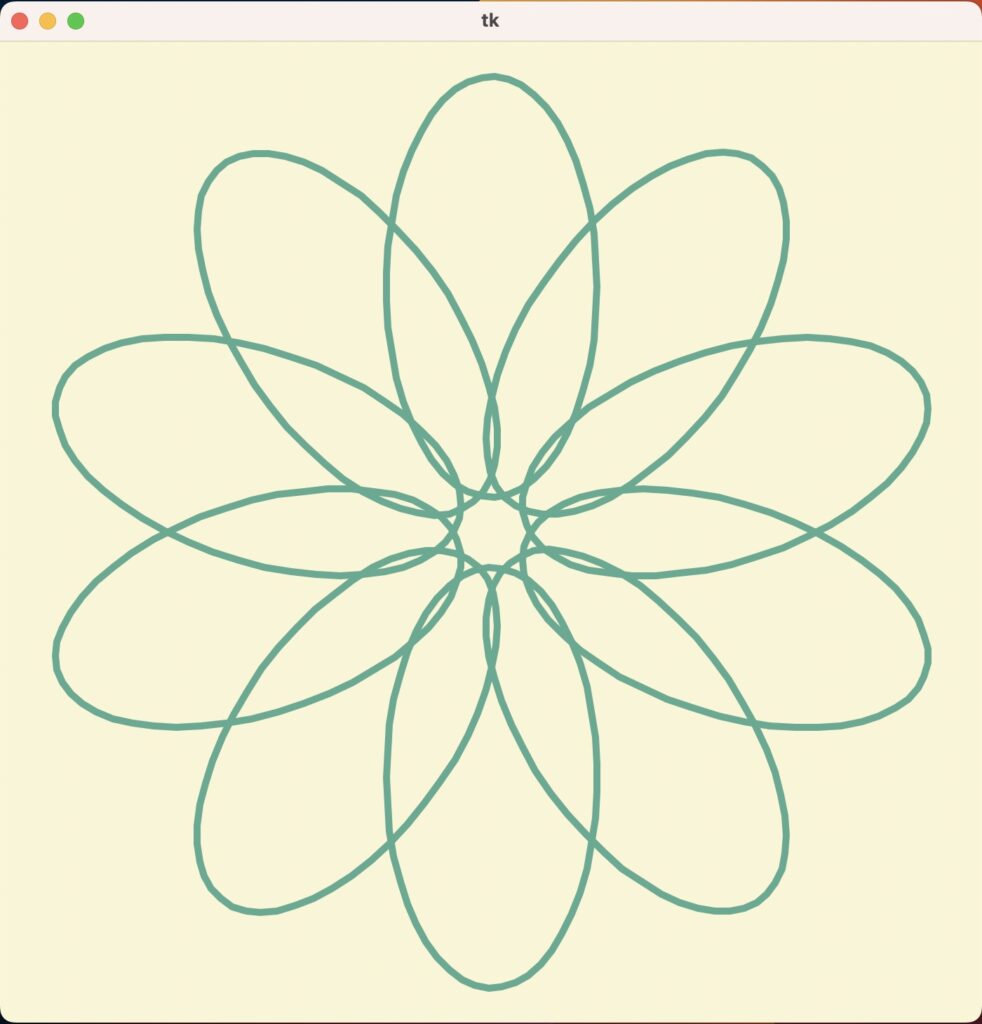
アート制作

これはお花を描くプログラムです。

一見複雑そうですが、楕円を回転させて位置をずらしながら配置しているだけです。

このような幾何学的な模様も、点の回転によって簡単に描けてしまいます。

お花模様を描くプログラムに関する記事は、近日中にアップするのでお楽しみに！

図形の回転

お次は図形をマウスドラッグにより回転させるプログラムです。

ExcelやWord等でこの光景を目にしたことがあるかも知れませんね。

現在Tkinter搭載の関数では、図形を回転させることはできません。

しかし、今回ご紹介した点を回転させるプログラムを上手く使うと、このようにクルクル回すことが出来るのです。

下記記事にて、Tkinterで図形を回転させる方法を紹介しています。

>> 【Tkinter】図形を回転させる！自動で回転・ドラッグで回転

まとめ

この記事では、$xy$座標平面上の点を回転させるプログラムをご紹介しました。

三角関数と複素数平面での解説を載せましたが、回転行列によっても回転が可能です。

現状の関数単体ではあまり有用性を感じられませんが、図形を回転する際には真価を発揮しそうです。

最後までお付き合いいただきありがとうございました。

この記事に関するお悩みや疑問・質問などは、ご自由にコメント欄に投稿してください(コメント欄はこの記事の最下部です)。

※頂いたコメントは全て拝見し、真剣に回答させていただきます！